상세 풀이 좀 부탁드립니다..ㅠㅠ
다음검색
댓글
댓글 리스트-
작성자성지훈 작성시간 15.09.24 13번. P(cos세타,sin세타) 이므로 직선 OP의 방정식은 y=x*tan세타 이고 Q의 y좌표가 sin세타 이므로 e^x-1=sin세타 에서
Q의 x좌표는 ln(1+sin세타). 그러면 T의 좌표는 T( ln(1+sin세타), ln(1+sin세타)*tan세타 )이므로 삼각형 ORT의 넓이인 S(세타)={ln(1+sin세타)}^2*tan세타 /2.
준식 = 세타가 0으로 갈 때 {ln(1+sin세타)}^2*tan세타 /2(세타^3) 에서 분모 분자를 (sin세타)^3으로 나누면
분자=1/cos세타, 분모=2 이므로 1/2cos세타. 세타가 0으로 갈 때 극한 값 a= 1/2. 따라서 50a= 25. -
답댓글 작성자Messi 작성자 본인 여부 작성자 작성시간 15.09.24 감사드립니다^^
-
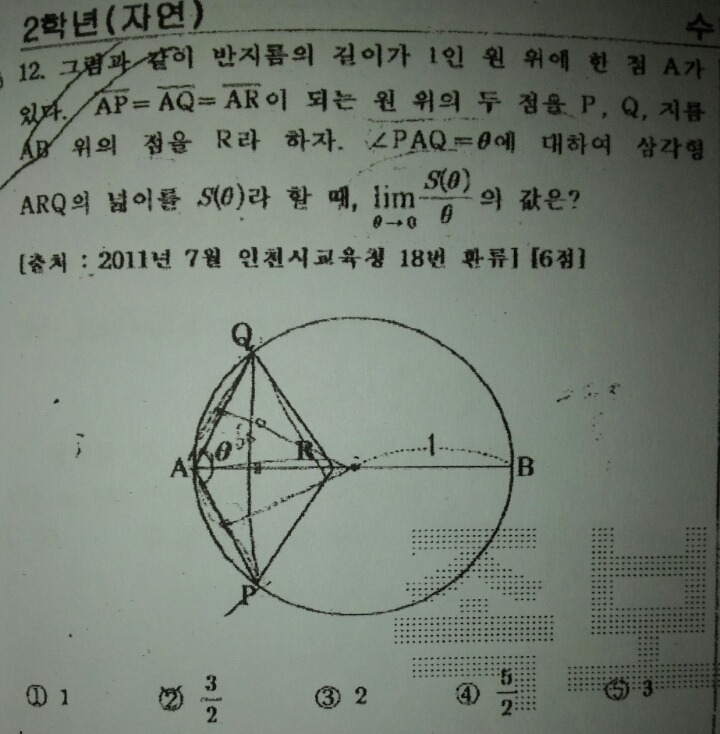
작성자성지훈 작성시간 15.09.24 14번. Q와 B를 연결하면 AB는 지름이므로 BQA=90도. 따라서 AQ=2cos(세타/2). 문제에서 AQ=QR이라 했으므로 ARQ의 넓이 S(세타)=1/2*sin(세타/2){2cos(세타/2)}^2.
따라서 준식= 1/2*sin(세타/2)/세타*{2cos(세타/2)}^2 = 1/2 * 1/2 * 4=1. -
답댓글 작성자Messi 작성자 본인 여부 작성자 작성시간 15.09.24 알겠습니다~바쁘실텐데 정말 거듭 감사드립니다^^