OFFSET 좌표점 구하기

[복받아요]

안녕하세요!

비구면 렌즈 제작 과정에서, 프로그래밍 부분에서 막히는 부분이 있어 질문올리게 되었습니다.

우선, 프로그래밍은 엑셀에서 함수값을 주어서 풀이를 할려고 합니다.

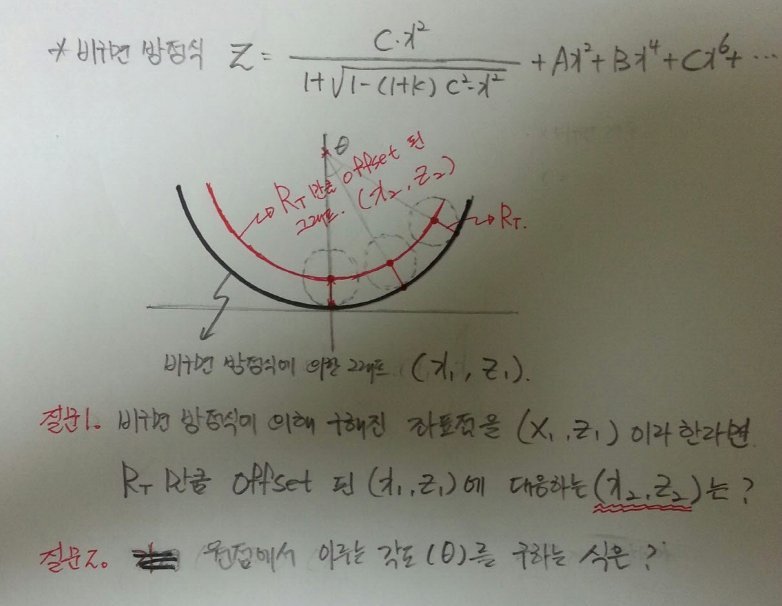
질문1. 아래의 비구면 방정식으로 주어진 비구면계수(C,K,A,B,C...)를 입력하여 (X1, Z1) 값은 구했는데,

         이 그래프를 공구값만큼 offset 시켰을때 (X1,Z1)에 대응되는 (X2, Z2) 값은 어떻게 구해야 하는지요?

질문2. 원점에서 (X1, Z1)에 해당하는 각 점에서의 각도(기울기)를 구하는 식은? 

           비구면 방정식을 미분해서 구해보고자 하였는데, 풀이가 틀린것 같습니다..

 

조언을 부탁드립니다.

[보이는것이전부는아냐]

z = f(x)꼴인데 왜 "(비)구면"의 방정식이라고 했는지 의아했지만, 그림의 z축으로 보이는 축으로 회전시킨 것이 본래의 모양이라고 보면 xz평면에 모델링해도 상관없을 듯해요.
이 때, 그림의 우측부분(x+ 부분)만 고려해도 무관해요. (x>=0)

z= f(x)일 때, tan-¹(-dx/dz) = ψ (-pi/2~0)로 놓고,
본래의 방정식을 만족시키는 임의의 점을 (xi, zi), 이 점이 offset 되는 점을 (xj, zj)로 놓으면,
xj = xi - Rcosψ, zj = zi - Rsinψ 이므로,
주어진 방정식에 xi = xj + Rcosψ, zi = zj + Rsinψ를 대입하면
x>=0 부분의 곡선이 offset된 곡선이 나와요.

[보이는것이전부는아냐]

2.
곡선 위의 임의의 점 (xi,zi)에 대해,
이 점에서의 접선과 법선이 각각 z축과 만나는 두 점과 이 점까지
세 점이 이루는 직각삼각형을 이용하면 각도 θ에 접근할 수 있는데,
다만 주어진 방정식이 멱급수의 형태인 것으로 보아 근사식으로 짐작할 수 있어요.
θ를 구하는 것은 곡면 내의 모든 점에 대해 법선과 z축이 만나는 점이
거의 일정한 것으로 볼 수 있는 허용범위에 있어야 의미가 있을 듯해요.