[수학](확통)경우의수 문제입니다. (연락처)

[최원수]

이번에 기출 문제인데 답이 잘 나오지 않아 질문 드립니다.

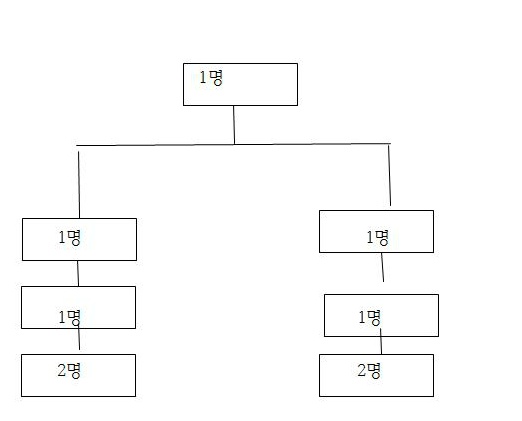
 9명의 비상연락망을 아래의 그림과 같이 작성하려고 한다.  가능한 경우의 수는 얼마인가?

저는 토너먼트로 해서

  9!/2!2!2! 으로 계산했는데  답이 아니네요  

세번째 1 명 1명 도 중복이 되는건가요?

[최원수]

평생충성~ 2! 두개는 마지막 두명의 자리들의 중복을 없애주는 것이고 나머지 2! 제일 위에서 두 갈래의 카테고리에서 중복을 없애 주기 위해 사용 하였습니다. 답은 선생님 의 답이 체크되어 있습니다. 정답인지 확신이 서지않아 미리 정답을 올리지 않았습니다. 전 분할 후 분배 방법으로 풀어보아도 45360가지가 계속 나오네요 ㅠ
죄송하지만 선생님은 어떻게 푸셨나요?

[수지기]

1층에 2명 2명은 순서가 없어서 9!은 좀 무리가 되는듯 합니다.
지정된 장소에 분배하는 것이라 (9C1)(8C1)(7C1)(6C1)(5C1)(4C2)(2C2)
또는 층별로 위부터 분할후 분배로 (9C1)(8C2*2!)(6C2*2!)(4C2*2C2/2! *2!)=90720
저도 답이 없어 자신이 없습니다. 그냥 제 생각입니다

[최원수]

분할을 할때 중복되는것을 없애야 될 거 같습니다.^^

[평생충성~]

문제가 문제가 있네요?
제가 풀어서나온 11340 은 대진표 분할분배 또는 중복제거하는 2! 나누기 했을때 둘 다 같은 답이 나왔는데요
지금 다시 직접 그려보니 쌤 풀이가 맞는것 같습니다.
두번째와 세번째의 1-1을 일반 대진표 방식으로 계산해버리면 11340 이 나오는데 이 두자리는 바꾸면 다른 경우가 됩니다. 중복되는 곳은 세군데가 맞습니다.

[성지훈]

ab-1-1-1-1-1-cd로 생각해서 전체 9!에 중복되는 경우는 ab가 자리를 바꾸는 경우, cd가 자리를 바꾸는 경우, 좌우반전되는 경우, 총 3가지이고 그 경우의 수가 모두 2이므로 2!을 세번 나눠줘야겠네요. 따라서 9!/2!2!2!이 맞는듯 합니다.