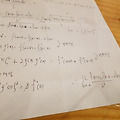댓글 리스트
-
작성자 졸다가 작성시간17.01.27 f"(a)가 존재하므로 f"(a)는 다음과 같이 나타낼 수 있다.
f"(a)=lim(k->0) (f'(a+k)-f'(a-k))/(2k)
••••••••••••••••••••••••••••(1)
또한, f(x)는 미분가능하므로 모든 실수 d에 대하여 f'(d)는 다음과 같이 나타낼 수 있다.
f'(d)=lim(k->0) (f(d+k)-f(d-k))/(2k)
여기에서 d 대신 a+k와 a-k를 각각 대입하면
f'(a+k)=lim(k->0) (f(a+2k)-f(a))/(2k),
f'(a-k)=lim(k->0) (f(a)-f(a-2k))/(2k)
이므로 이것을 (1)식에 대입하여 정리하면
(극한은 중복되는 기호이므로 한 번만 사용)
f"(a)=lim(k->0)(f(a+2k)-2f(a)+f(a-2k))/(2k)^2
여기에서 2k=h라 놓으면
f"(a)=lim(h->0) (f(a+h)-2f(a)+f(a-h))/h^2