|
이전 포스트에서는 95% 신뢰구간을 중심으로 알아봤습니다. 하지만 신뢰구간을 길이를 늘리는 것도 물론 가능합니다.
예를 들어 99% 신뢰구간이라면 신뢰구간을 많이 뽑았을 때 이론적으로 99% 갯수(1000개면 990개, 10000개면 9990개)의 신뢰구간이 모평균을 포함한다는 말이 됩니다. 하지만 신뢰구간의 길이가 길어지면 신뢰구간이 모평균을 포함할 확률이 높아지지만 실제적인 효과는 줄어들 수 있습니다. 여기서 서로 다른 퍼센테이지를 신뢰수준(confidence level)이라고도 칭합니다.
예를 들어 어느 대선후보의 득표율을 신뢰구간으로 알아본다고 할 때, "20%에서 98%사이로 득표할 것으로 보입니다"라고 하면 정말 별 도움이 안 되겠죠. 신뢰구간은 엄청 넓어서 모집단의 득표율이 안전하게 포함되지만 실제로는 별 쓸모없는 신뢰구간이 되는 것입니다. 모평균이 포함되는 비율을 95%에서 99%로 늘릴 때는 항상 이 점을 염두에 두고 살펴보시기 바랍니다.
일단 95% 신뢰구간은 한 쪽 길이는 1.96 곱하기 표준편차였는데요. 99%에서는 얼마인지 알아보도록 하겠습니다.
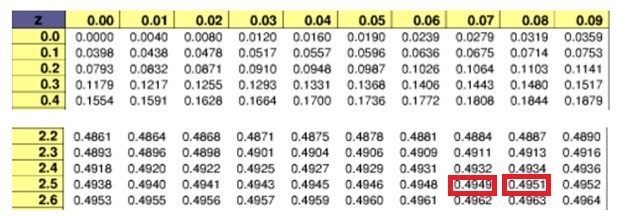
표준정규분포표에서 2.5와 0.07을 연결시키면 0.4949가 나옵니다. 그리고 2.5와 0.08을 연결시키면 0.4951이 나옵니다. 그 가운데수는 0.4950이 되어 곱하기 2를 해주면 0.99가 되죠. 따라서 99%에 해당하는 z값은 2.57과 2.58의 중간인 2.575가 되는 것입니다.
아래는 정규분포에서 95%와 99%가 차지하는 넓이를 비교해본 것입니다.
99%가 확실히 노란 부분이 x축에서 차지하는 길이가 95%보다 더 긴 것을 알 수 있습니다. 99%에서는 신뢰구간이 넓어진 만큼 더 많은 신뢰구간이 모평균을 포함하게 됩니다.
일반적으로 신뢰구간에 나오는 퍼센테이지를 그리스문자 알파를 이용해 아래와 같이 표시합니다.
예를 들어 알파가 .05라면 신뢰구간은 95%짜리가 되고 알파를 2로 나눈 것은 0.25, 그리고 여기에 해당하는 z값은 1.96이 되는 것입니다.
여기서 2로 나누는 이유는 위의 정규분포 그림을 보시면 아시겠지만 노란부분의 면적을 빼고 좌우로 남는 부분이 있습니다. 여기서 알파는 좌우로 남는 부분의 면적을 합한 것과 같습니다. 95%짜리에서는 전체 면적은 1, 노란부분의 면적은 .95, 남는 부분은 .05가 되겠죠. 남는 부분은 두 개로 갈라져 있습니다. 따라서 곡선 왼쪽 끝에서부터 노란부분까지의 면적은 0.5를 2로 나누어야 하므로 0.025가 되고 곡선 오른쪽 끝에서부터 노란부분까지의 면적도 역시 0.25가 되는 것입니다.
90%, 99%도 마찬가지로 해석하시면 되겠습니다.
이제 신뢰구간이라는 것을 일반적으로 표시해보면 다음과 같습니다.
표본평균의 양옆으로 구간을 만들어 준 것이 보이네요. 가운데 z값부터의 표현은 이전에 보았던 1.96sd를 수식으로 표현한 것이라고 보시면 됩니다. z값은 위의 표를 보시면 신뢰구간의 길이에 맞게 나와 있습니다.
|
|
설문조사로 지지율같은걸 알고싶다고 하죠. 그 가상의 지지율을 p라고 부르겠습니다.
p의 95% 신뢰구간은 p +- 1.96 * sqrt{ p*(1-p) / n } 입니다.
sqrt는 "루트"입니다. sqrt(4)=2, sqrt(9)=3 이런 루트요.
여기서 오차한계 = "1.96 * sqrt{ p*(1-p) / n }" 입니다. 정규분포에서 Pr( |Z| < 1.959964) = 0.95여서 95% 신뢰구간은 1.959964와 마찬가지인 1.96을 사용한겁니다.
99%인경우 2.575829를 사용합니다.
95%신뢰수준에서 오차한계가 3%(0.03) 란 말는 한예로 조사결과 p=0.6이라고 나왔을때 조사후 95%신뢰구간을 얻었을때, (상한, 하한)이 최소한 (0.6-0.03, 0.6+0.03) = (0.57, 0.63)을 얻고싶다는 말입니다.
여기서 지지율 p를 알고 신뢰구간과 오차한계만 주어지면 오차한계 = 1.96*sqrt{p*(1-p)/n}에서 n을 구할수있습니다.
그런데 조사도 안했으니 p를 알수가 없죠. 그리고 한 조사로 아닌 여러가지 비율을 조사할 예정이면 알더라도 어떤 비율을 써야할지 알수가없지요.
그래서 p는 최악의 경우인 0.5를 사용합니다. 최악의 경우라한것은 p*(1-p)이 p=0.5일때 최대가 되기때문입니다. 이경우 n이 가장 커져야하고, 오차한계도 가장 커집니다.
p=0.5이면 p*(1-p)=1/4가 되어 오차한계 = 1.96/2/sqrt(n)
n에 대해서 풀면 n = (1.96/2/오차한계)^2 입니다. ( "^2"는 "제곱"입니다.)
오차한계가 3% 즉 0.03이면 > (1.96/2/0.03)^2
5% 즉 0.05이면
8% 즉 0.05이면 실제로 사용할때는 소수점 올림을 해서 사용합니다. 즉 8%의 경우 151의 표본이 필요합니다. |
표본의 크기를 결정하기 위한 첫 번째 절차는 원하는 신뢰수준과 신뢰구간
의 폭을 결정하는 일인데, 이러한 의사결정은 수용될 수 있는 불확실성의 크
기, 불확실성을 감소시키기 위해 수반되는 비용, 오류가 야기시키는 비용에
관련된다.
마케팅 조사는 그릇된 의사결정으로부터 야기되는 손실에 대하여 의사결정
자가 갖은 유일한 대응이므로, 마케팅조사의 비용은 그릇된 의사결정의 위험
을 감소시키기 위한 비용으로 인식되어야 하며, 신뢰수준과 신뢰구간의 폭을
결정하는데 있어서 가장 중요한 요소로 작용한다.
이론적으로는 표본조사의 한계비용이 조사결과 정밀성에서 기대되는 한계
이익과 같아지는 표본의 크기를 선택해야 하지만, 직관적으로는 마케팅 의사
결정이 많은 위험을 내포하고 그릇된 의사결정의 비용이 클수록 신뢰수준을
높게 결정하며 신뢰구간을 좁히기 위하여 대표본을 사용한다.
마케팅 의사결정에 있어서는 대체로 95%의 신뢰수준이 사용되는데, 이는
진정한 모집단의 모수가 신뢰구간에 의해 규정한 범위를 벗어날 확률이 5%
미만임을 나타내는 것이다.
그러나 모집단 보수를 추정하는데 있어서 표본조사의 크기(E)를 인정하는
일은 조사자가 모집단의 모수 자체에 관한 정보를 갖고 있지 않기 때문에 대
단히 어려우며, 더욱이 추정된 모수의 값이 의사결정의 기준치와 유사할 때
민감한 문제를 야기시킨다.
예를들어, 선반기계의 손익분기점이 100단위일 때 표본조사를 통해 예측된
수요가 이러한 값과 유사한다면 단지 10단위의 오차라도 파산과 막대한 수익
사이의 차이를 의미하게 되므로 다소의 조사비용을 감수하더라도 표본의 크
기를 증대시켜 신뢰수준을 높이거나 신뢰구간의 폭을 좁혀야 할 것이다.
이러한 딜레마에 대응하기 위한 한가지 방법은 축자표본추출(sequential
sampling)인데, 조사자는 우선 작은 표본을 사용하여 모집단의 모수를 추정하
여 만일 그 값의 의사결정의 기준치에 유사할 경우라면 표본의 크기를 증대
시켜 다시 모수를 추정할 수 있다.
물론 표본의 크기를 증대시켜 추정한 모수가처음 추정한 모수와 별다른
차이를 보이지 않을수 있지만, 그러한 모수를 추정할 수 있다. 물론 표본의
크기를 증대시켜 추정한 모수가 처음 추정한 모수와 별다른 차이를 보이지
않을 수 있지만, 그러한 모수의 신뢰구간은 표본의 크기가 증대되었으므로 좁
혀질 것이다.
신뢰수준은 모집단으로부터 표본을 추출하여 조사한 결과로 조사된 결과대로 결과가 나올 예상 확률이다.
예를 들어서, 95%의 수준의 신뢰수준이라고 하면 100번의 설문조사의 결과중 해당되는 결과가 95번이 나올 확률이다.
대통령 후보간 지지율이 A후보 35%, B후보 20%를 95% 신뢰수준에서 표본오차 ±3% 포인트로 결과가 나왔다면 A후보는 35%에서 앞뒤 3% 차이의 값을 얻어 32%~38%사이의 비율이고 B후보 지지율은 20%에서 앞뒤 3% 차이의 값을 얻어 17%~23% 사이의 비율일 것이란 의미이다. 보통은 95%의 신뢰도를 사용한다. 100번 조사했을 때 앞에서와 같은 결과가 95번 나온다는 것이다.
그리고 표준오차는 같은 모집단에서 표본을 추출하여 설문조사를 하더라도, 표본은 조사때마다 서로 다르다.. 이 서로 다름을 표준오차라고 하며, 표준오차=표준편차/표본수로 계산하여 설문조사 결과에 덧붙여진다.
전체국민을 대표할 수 있는 표본을 잘 추출한다고 해도 표본을 대상으로 측정한 수치는 전체 국민의 실제 수치 간에 차이가 발생할 수밖에 없다. 바로 이차이를 표본오차라고 한다. 오차는 실수를 범한다는 의미의 오류가 아니라 표본을 사용하는 여론조사에서 얻어지는 근사치의 범위를 의미한다. 표본오차는 표본의 수에 따라서 달라진다. 여론조사에서 표본오차는 그 조사의 신뢰도와 정확성을 판단할 수 있는 척도로써, 언론에서 여론조사를 한 후 그 결과를 알릴 때 표본오차와 신뢰수준을 반드시 밝히는 이유가 여기에 있다.
응답률이 저조하다는 것은 표본수가 충분치 않았다라고 생각할 수 있다.
이는 모집단의 성향을 충분히 반영하지 못한 것이기에 결과에 대한 신뢰도는 응답률이 높은 설문조사에 비해 떨어지게 된다.
통계에서의 신뢰도는 일반적인 개념에서의 신뢰도와 그 용법이 다르다 할 수 있습니다.
신뢰수준을 설정하고, 오차범위를 뽑아내는 복잡한 수학 이론은 배제하고 의미위주로 보자면....
(고등학교 때 통계 배웠던 것을 떠올리시면 더욱 확실하게 이해되시리라 생각됩니다.)
위에 보시면 95% 신뢰수준 +-2.5%라고 되어있습니다.
한열사에 올라오는 글, 리플을 보면 많은 분들이 저 결과를 신뢰할 수 있는 수준이 95%다 라고 받아들이시는 것 같은데,
그 뜻이 아닙니다.
통계에서의 신뢰수준(신뢰도) 라는 것은 값이 오차범위(+-2.5%)안에서 나올 확율을 말합니다.
예를 들어 여론조사 결과 A후보의 지지율이 50%가 나왔는데 그 표집오차가 신뢰수준 95%에 +-2.5%라고 하면
같은 방식으로 100번을 조사하면 95번은 47.5% ~ 52.5% 사이에서 나올 것이라는 뜻입니다.
즉, 신뢰도라는 것은 '참값'에 가까운 정도를 의미하는 것이 아니라 동일한 조건에서 재차 반복하여 조사를 했을 경우 표본오차범위 내에서 그 값이 나올 가능성을 말하는 것입니다.
그러므로 여론조사를 진행할 때 진행방식, 설문문구 등에 오류가 발생되면 신뢰도가 높더라도 타당도(참 값에 가까운 정도)가 낮아져 참 값에서 벗어난 여론조사 결과가 나올 수 있는 것입니다.
누구맘대로 신뢰도, 오차범위를 정하는거냐 하시는 분은 http://navercast.naver.com/contents.nhn?contents_id=2784 에서 친절하고 수학적인 설명을 얻으실 수 있습니다.