5. Vincenty 식의 적용 및 특성
이전 글(1부)을 게시한 후 댓글 대화를 통해 보다 정확한 식체제인 Vincenty식[3]을 알게 되어 이 식으로도 계산체제를 구성하여 조사를 수행한 것입니다. (처음 계획했던 것보다 훨씬 더 깊이 測地에 들어가버렸네요)
비교 대상은 지도SW 중 거리제시 숫자가 제일 많은 Google Earth와 현재까지 제시된 식 중 가장 정확하다는 Karney 식[4]에 의한 거리입니다. 이 식에 의해 거리계산을 제공하는 site가 있는 데(7 항에서 다시 언급) site의 화면을 보면 아래 그림과 같이 계산된 거리 출력의 정밀성을 선택하게되어 있는 데 그 정도가 mm도 아닌 nm까지 있는 걸 보면 정확성이 대단한 가보다는 느낌을 줍니다.

실제로, 여러 거리계산 방법들의 정확성을 이 식을 기준으로 평가하는 학술논문[5]이 있는 것을 보면 측지학계에서의 평가도 역시 Karney 식을 매우 정확한 식으로 보고 있는 것 같습니다. 여기서도 Karney식 결과를 정확성 평가의 기준으로 하고 이야기를 진행합니다.
비교결과는 아래 표1에 있고 1부에서 언급했던 Wikipedia식 기반체제[(1),(2)식]는 정리의미에서 함께 수록했습니다.
표1. 두 지점간 거리계산 방법들의 특성조사
| 경우 | 비교인자 | Karney식[4] | Google Earth | Vincenty식[3] | (1),(2)식 | ||
| 서로다른 경위도 두 지점간 | Crlam | 1.00E-05 | 1.00E-07 | 1.00E-11 | |||
| 거리,km | 1480.283158 | 1480.29 | 1480.28209 | 1480.28316 | 1480.283158 | 1480.836855 | |
| Karney식과 차이,km | 0.01 | -1.E-03 | -2.E-06 | 2.E-07 | 0.55 | ||
| Karney식과 차이,% | 5.E-04 | -7.E-05 | -2.E-07 | 1.E-08 | 0.037 | ||
| 반복횟수 | 2 | 3 | 4 | ||||
| dLamda | 6.E-07 | 1.E-09 | 3.E-12 | ||||
| 동일 위도선상의 경도간 거리 | Crlam | 1.00E-05 | 1.00E-07 | 1.00E-11 | |||
| 거리,km | 2269.016219 | 2269.02 | 2268.999374 | 2269.01617 | 2269.016219 | 2271.669927 | |
| Karney식과 차이,km | 0.004 | -2.E-02 | -5.E-05 | 2.E-07 | 2.654 | ||
| Karney식과 차이,% | 2.E-04 | -7.E-04 | -2.E-06 | 1.E-08 | 0.12 | ||
| 반복횟수 | 2 | 3 | 5 | ||||
| dLamda | -3.E-06 | -8.E-09 | -6.E-14 | ||||
| 동일 경도선상의 위도간 거리 | Crlam | 1.00E-05 | 1.00E-07 | 1.00E-11 | |||
| 거리,km | 1768.406319 | 1768.42 | 1768.406319 | 1768.40632 | 1768.406319 | 1768.415551 | |
| Karney식과 차이,km | 0.01 | 2.E-07 | 2.E-07 | 2.E-07 | 0.01 | ||
| Karney식과 차이,% | 8.E-04 | 1.E-08 | 1.E-08 | 1.E-08 | 5.E-04 | ||
| 반복횟수 | 1 | 1 | 1 | ||||
| dLamda | 0.E+00 | 0.E+00 | 0.E+00 | ||||
먼저 이야기가 짧을 Google Earth(GE). GE는 거리계산치는 앞 1부 작성시 조사했던 것으로 당시는 거리오차의 관심정도가 이번처럼 높지 않아 계산결과 기록의 최소숫자가 10m. Karney식과의 차이가 Vincenty식보다 현저하게 더 큰 이유의 주된 이유가 거리계산 방법 차이 이전에 이것 때문인 것으로 여겨지네요.
Vincenty식은 반복법이 요구되고 또 식에 대한 설명에서 수렴성 문제가 언급되어 있어 망서렸으나 프로그램을 작성하여 계산을 해보니 수렴성이 위 표에서 알 수 있듯이 굉장히 좋더군요. 거론된 수렴성 문제는 지구의 정반대편 지역간(예:대전과 Buenos Aires 간) 계산에만 한한 듯 하네요.
위 표의 인자는,
- Crlam: Vincenty식 은 여러 식으로 구성되어 있고 계산되는 인자 중 하나가 Lamda인데 반복법에서 Lamda 변화량이 어느 값이하가 될 때까지 반복계산을 수행할 것인가를 지정하는 인자.
- 반복횟수:실제 이루어진 반복계산 횟수
- dLamda:반복계산이 종료된 상태에서의 Lamda의 변화량
반복계산은 가속인자(relaxation factor)나 기법 사용없이 단순반복계산이었는 데 불과 4회에 dLamda는 10^-12 크기로 급격히 감소.
그리고 정확성에서는, Karney 식 계산결과와는, 경,위도가 다 다른 ~1800km 떨어진 두 지점간의 거리에서 거리차이가 10^-6km= 1mm, %로는 10^-7%. 참고문헌[3]에 의하면 Vincenty식의 정확도는 0.5mm. (참고로 이러한 수식들에 계산되는 지구표면상에서의 실제 거리가 아니라 가상적 또는 이상적인 지구모형 표면에서의 거리. 그러기에 지구상 거리에서 0.5mm정도의 오차라는 말이 있을 수 있는 것이겠지요.)
6. Wikipedia 거리식과 다른 지도 SW와의 거리 차이 이유
1부에서 거론한 경위도간 거리에 대한 식의 계산 결과에서 Wikipedia에서 온 식인 동일위도선상의 두 지점간 거리식인 (2)식에 의한 거리와 다른 SW와의 거리 차이가 0.1%로 동일 경도 두 지점간 거리 차이0.004%보다 현저하게 커 2)식이 엄밀식이 아닌 개략식이 아닐까 했었는 데 1부 댓글대화에서 2)식이 엄밀식이라는 이야기에 2)식을 구체적으로 조사해보았지요.
조사해보니, 2)식은 개략화가 들어가지 않는 타원체에서의 엄밀식, 그러면 타원체와 다른 지도 SW에서 사용했을 가상적 지구모형인 WGS84의 모형과 차이가 있는가? 그런데 WGS84모형을보니 모형의 타원체도 단지 단반경과 장반경 두 인자로만 정의되는 일반적인 타원체, 즉 변형이 없는 타원체 모형. 그러다 생각나는 게 Karney 식이나 Vincenty식이 두 지점간의 최단거리를 계산하는 식이라는 점. 최단거리.. 그래 지도상의 대각선길이와 구형체표면에서 최단거리와는 차이라는 게 있을 수 있지 하지만 등위도상의 두 지점인데? 그러다 지구본을 쳐다보니 등위도상의 두지점간의 최단거리 궤적이 등위도선이 아닐 수 있더군요.
아래 그림에서 아래 노란선이 Google Earth가 등위도선상의 두 지점의 거리 계산시 그린선. 등위도선과는 확실히 차이가 있고 그 길이가 등위도선상의 길이보다 작음을 느낄 수 있습니다.
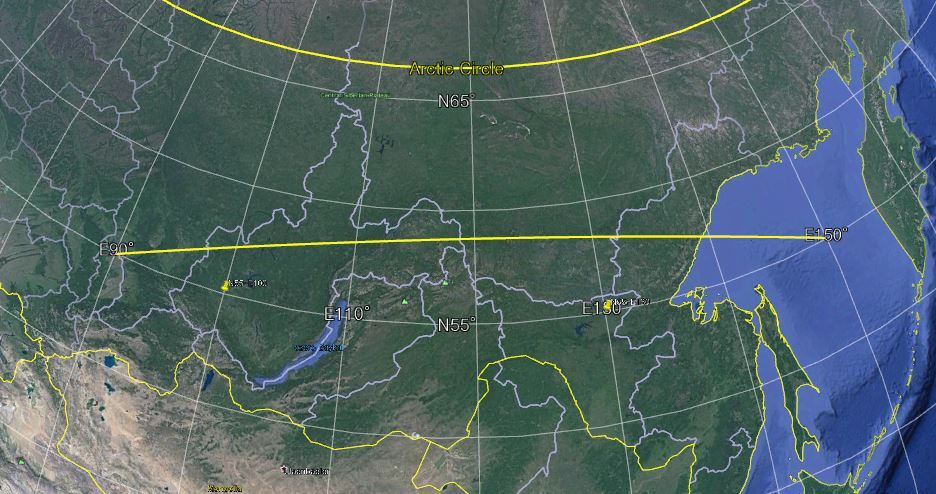
요약하면 2)식은 개략식이 아니라 엄밀식인데 그 식의 대상이 등위도의 두 지점을 등위도선을 따라 잇는 선의 길이, 현실적인 표현으로는 평면지도상의 최단거리. 이에 비해 Google Earth와 같은 지도 SW에서의 거리는 지구 타원체 모형에서 두 지점을 최단으로는 잇는 선의 길이, 달리표현하면 말그대로 두 지점간의 최단거리.
참고로 (2)식의 유도과정에 관심이 있다면 자료[1]의 'Length of a degree of latitude', 'Geocentric latitude, Parametric (or reduced) latitude' 그리고 [8]의 '5.5 The reduced or parametric latitude'을 참조
아래 그림은 이러한 차이의 특성을 파악하기 위한 것으로서, 위도에 따른 차이(붉은 실선:거리차이 자체, 청색실선:%)와 2)식에 의한 등위도에서 경도1도 떨어진 지점간의 거리(흑색 점선)입니다.

그 차이는 위도에 따라 변하는 데 차이자체는 ~55.7도에서 최대가 되고 그 값은 0.55m. 이에 비해 차이의 비율은 위도증가에 계속 증가하여 극지역에서 1.3%에 도달
등위도 지점간에는 등경도 지점간의 이러한 차이가 없기에 1)식은 지도 SW에서 계산하는 거리와 같은 종류의 거리가 되고 이에 따라 거리계산 결과에서 2)식에 의한 차이가 1)식에 의한 차이보다 현저하게 컸었던 것.
7. 경위도 차이에 따른 바람직한 계산체제 구축에 대한 조언
거리계산 체제를 갖추고자 할 때 고려대상으로 1),2)식 기반체제와 Vincenty식 체제가 현실적인 고려대상 체제로 여겨집니다.
먼저 1),2)식 체제는 앞에서 이야기한대로 수식자체가 평면지도상의 거리로 가상적 거리를 계산하는 체제. 이에 비해 구하고자하는 거리가 통상적으로 생각하는 두 지점간의 실제 거리인 최단거리이라면 이는 먼저 거리의 의미차이로 인해 등위도 거리에서 최대1.3%의 오차, 우리나라 위도지역에서라면 ~0.4% 오차를 안게 됩니다.
그 다음 수식계산체제의 구축관점에서 보면, 1),2)식 체제는 사용되는 식이 2개로 일단 간단해보이는 반면 Vincenty식 체제는 이보다는 훨씬 더 많은 식을 사용합니다.
하지만 1)2)식체제는 거리계산 대상의 두 지점을 잇는 선을 작은 구간으로 나누어 경도상 차이거리와 위도차이 거리를 각각 구하여 이로부터 대각선의 길이를 구하여 더해가는 선적분을 수많은 구간에 대해 해야합니다. 이에 비해 Vincenty식 체제는 비록 수식갯수는 훨씬 더 많고 또 반복법이 필요하지만 1)2)식체제에 요구되는 전산해석적 선적분이 필요하지 않고 또 경도,위도 간 거리를 따로따로 구하는 게 아니라 한번에 구하는 방식이기에 프로그램길이는 ~20% 정도만 더 긴 정도. 인쇄를 한다면 불과 A4용지 1~1.5장 정도.
그래서 어느 정도 정확성을 유지하는 가운데 경위도 간 거리를 구하는 자신의 계산 체제를 갖추고자 한다면 Vincenty식을 Excel화 시키는 게 좋은 것으로 여겨집니다.
또 굳이 체제를 갖추지 않고 정확성이 높은 값을 알고자한다면 정확성 평가의 기본이 되기도하는 Karney식 체제에 의한 거리계산 site[6]가 있으니 이를 이용. 표1의 Karney식 체제 거리도 이 site에서 계산한 값입니다.
그리고 Vincenty 식 경우는, 이 식을 이용하여 거리 등을 계산하는 Excel 프로그램 파일을 제공하는 site[7]가 있으니 굳이 자신이 프로그램까지는 하지 않아도 되지만 internet연결과 무관한 편리성이 필요한 경우라면 이를 사용하는 것이 좋은 방법이 될 것 같네요.
8. 인용문헌
[1]. Latitude, https://en.wikipedia.org/wiki/Latitude
[3] Vincenty's formulae, https://en.wikipedia.org/wiki/Vincenty%27s_formulae
[4] Algorithms for geodesics,Charles F. F. Karney,J. Geodesy 87(1), 43?55 (Jan. 2013); https://geographiclib.sourceforge.io/geod.html
[5] 이용창, 측지 역 문제 해석기법의 정확도 분석, http://koreascience.or.kr/article/JAKO201134036358128.page, 2011.08.30
[6] Online geodesic calculations using the GeodSolve utility, Charles Karney,https://geographiclib.sourceforge.io/cgi-bin/GeodSolve?type=I&input=25.05518333+121.5129667+37.562+126.9772833&format=g&azi2=f&unroll=r&prec=3&radius=6378137&flattening=1%2F298.257223563&option=Submit
[7] GEODETIC CALCULATION METHODS, Geoscience Australia, http://www.ga.gov.au/scientific-topics/positioning-navigation/geodesy/geodetic-techniques/calculation-methods
[8] Osborne, Peter (2013). The Mercator Projections. doi:10.5281/zenodo.35392. for LaTeX code and figures., 2013, https://zenodo.org/record/35392#.YEjPO9IzZhE
(*필요하다면 자유롭게 복사/스크랩 해가서출처를 밝히고서 잘 활용하세요. 흔적을 남겨주면 더욱 좋겠지요?)
남겨주면 더욱 좋겠지요?)
댓글
댓글 리스트-
작성자산타바 작성시간 21.03.11 그 새 연구 많이 하셨네요... 본문과 관련하여 약간 첨언 드리면, karney식이 더 정확한 것은, 실제로는, vincenty식 보다, f(편평률)와 관련한 멱급수 항을 좀 더 고차항까지 포함시켰기 때문입니다.
vincenty 식의 수렴이 늦어지는 경우는, 극지방에 대한 계산일 때가 아니라, 대척점 부근에 대한 계산(측지거리 ~20000km)일 때입니다.... -
답댓글 작성자나무 작성자 본인 여부 작성자 작성시간 21.03.10 karney식 정확성, 그런가요? 수렴성, 확인해보니 그렇네요. 지적 고맙습니다. 여담입니다만, 이번 작업전에는 측지학이라는 말에 측지학? 學이라고까지 할 게 있는건가? 했었는 데 이번 작업을 통해서 그래 學이라고 할 수도 있겠네 해지더군요.