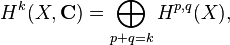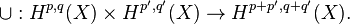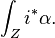호지 추측은 대수기하학의 주요 미해결 문제 가운데 하나로 특이점이 아닌 복소 대수다양체의 대수적 위상에 관한 문제이다. 가설의 개요는 드람 코호몰로지 모임들이 대수적이라는 것이다. 다른 말로 표현하면 이 모임들은 변형 코호몰로지 모임인 푸앵카레 쌍대의 합으로 나타낼 수 있다는 것이다. 클레이 수학연구소는 호지 추측을 밀레니엄 문제의 하나로 선정하였다.
도입
X를 n차원의 복소차원에 대한 연결공간 상의 컴팩트한 복소다양체라 하면 X는 2n 차원의 가향인 매끈한 미분다양체(orientable smooth manifold)가 된다. 따라서 이들의 코호몰로지 군은 0도에서 2n 사이에 놓이게 된다. 이제 X를 켈러 다양체라 가정하면 이들의 코호몰로지는 다음과 같이 나타낼 수 있다.
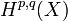가 형(p,q)의 조화 형식으로 표현되는 코호몰로지 모임들의 부분군인 경우 특정 좌표 
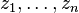의 미분 형식으로 표현되는 코호몰로지 모임들은 조화 함수의 곱 
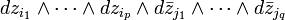으로 기술할 수 있다.(상세한 내용은 호지 이론을 볼 것.) 코호몰로지 상의 컵곱에 상응하는 조화 형식의 쐐기곱을 취하면 컵곱은 다음과 같이 호지 분해로 변환된다.
X가 복소다양체이므로 x에는 기초 모임(fundmental class)이 있다.
Z를 k차원의 X에 대한 복소 부분다양체라 하고 i : Z → X라 가정할 때 형(p,q)의 미분 형식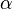 
는 다음과 같이 적분된다.
이 적분을 살펴보면, 한 점 Z를 취하여 이를 0라 할 때, 0 주위에 있는 X상의 좌표 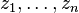를 선택하면 Z는 
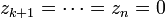이 된다. p > k일 경우 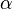는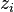 
이 영이 되는 Z상의 
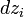를 반드시 포함하여야 한다. 따라서 (p, q) ≠ (k, k)이면 이 적분은 영이 된다.
보다 추상하면 이 적분은 Z의 호몰로지 모임과 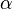로 표현되는 코호몰로지 모임에 대한 모자곱이라 기술할 수 있다. 푸앵카레 쌍대에 의해 Z의 호몰로지 모임의 짝이되는 코호몰로지 모임을 [Z]이라 할 수 있다. 그리고 이 모자곱은 [Z]와 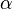의 컵곱에 X의 기본 모임을 모자곱하여 계산할 수 있다. 코호몰로지 [Z]는 호지 분해되기 때문이다. 이상과 같이 이 모임에 형(p, q) ≠ (k, k)인 임의의 모임을 컵곱할 경우 영이 됨을 알 수 있다. 따라서 
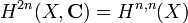이기 때문에 [Z]은 
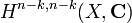안에 놓여있어야만 한다. 느슨하게 말하면 호지 추측은 다음과 같이 표현된다.
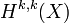안의 코호몰로지 모임은 복소 부분다양체 Z에서 도출될 수 있는가?