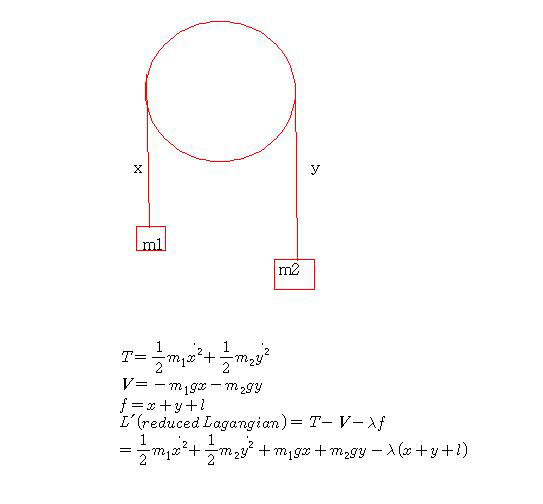
위의 위치에너지의 기준점은 도르래 중심입니다. (어디를 잡든 상관이 없기에)
구속조건을 쓸때는 보통의 라그랑지안이 아닌 리듀스라그랑지안을 쓴답니다.
라그랑지안은 정말 파워풀한 풀이 방법입니다.
물체에만 쳐다보고 운동에너지랑 위치에너지를 기술한뒤
그 뒤부터는 아무 생각없이 수학만 계속 하면 모든 결과값들이 수두륵하게 쏟어져 나옵니다.
별로 복잡하지 않습니다.
한번쯤 해보심이 좋을듯 보입니다.
운동방정식까지 다 쓰고 결론까지 내려고 했지만.
문제푸는것은 몇분 안걸리는데.... 이게 보여드릴려고 한글에서 식 적는대만 몇십분 잡아먹군요 ㅠ
그래서 그건 생략하겠습니다.
많은 분들이 도움이 되셨으면 합니다.
다음검색
댓글
댓글 리스트-
답댓글 작성자00 릴라~! 작성자 본인 여부 작성자 작성시간 09.10.30 에프부터 설명을 해야 할듯 보입니다...에프는...우리가 흔히 운동방정식을 바로 풀때 사용하는 구속조건에 해당되는 방정식입니다...여기서는 실의 길이겠죠....x+y=l 입니다...라그랑지안을 만들때(?) 헤밀토니안 식에 구속조건 방정식앞에 변수가 들어가야 하는 데 그 변수가 람다입니다....람다에프를 넣고...풀어보니깐....그 람다가 어떤 구속조건에서 나오는 힘이라는 것이죠......사실 정확히 말하면 람다가 힘은 아닙니다...람다 라운드f /라운드 q 가 힘입니다.....하지만 여기서 뒤에 라운드f/라운드q가 1이 되어 람다가 힘인것처럼 나오죠..만약 토크라면...라운드f/라운드q 가 1이 아니고 길이차원을 가진 어떤 녀석이 나오겠죠
-
작성자피흘리는겨울 작성시간 09.10.30 짝짝짝...여기 저기 까페 많이 돌아다녀봤는데.. 물화생지 만한 곳이 없던데...님같은 분이 계셔서 물화생지가 젤 수준이 뛰어난 것 같네요...^^:
-
답댓글 작성자00 릴라~! 작성자 본인 여부 작성자 작성시간 09.10.30 ^^;;;;;; 감사합니다.
-
작성자나를알자 작성시간 09.10.30 와!! 구속 조건을 쓰려면 변위를 x, l-x이렇게 두면 안되는군요~ 많이 보던 장력식이 나와서 반갑네요~이중 도르래면 세 질량을 다 다르게 놓아야 하니 복잡해지겠군요! 라그랑지안은 정말 대단합니다 ㅎㅎ 이중 도르래는 나중에; 시간이 나면 해봐야겠어요. 잠이 오거나 할때ㅋㅋㅋ 릴라님 정말로 감사합니다! 한글에서 문자쓰는거 진짜 힘드실텐데^^
-
작성자엠마 작성시간 09.10.31 우와~ 정말 대단하세요. 릴라님... 항상느끼는거지만 존경스러워요.