안녕하세요?
논란이 계속 되네요. 그래서 용수철 저울이 질량이 있을 경우를 생각하여 예를 들어 계산해 보았습니다.
용수철이 늘어난 길이는 용수철을 이루고 있는 입자간 간격들을 모두 더한 것이 될 것인데요,
그 입자간 간격이 크지 않아서, 그 간격 하에서 입자들 사이의 힘이 일차함수적으로 근사할 수 있다고 가정하였습니다.
그래서 용수철만 매달려 있는 경우와, 무게 F를 주었을 때와, 무게 2F를 주었을 때의 길이변화를 구해서
과연 길이변화가 무게에 비례적으로 나타나는지 파악하려 했습니다. (비례적으로 나타난다면 용수철상수는 일정하다고 볼 수 있음)
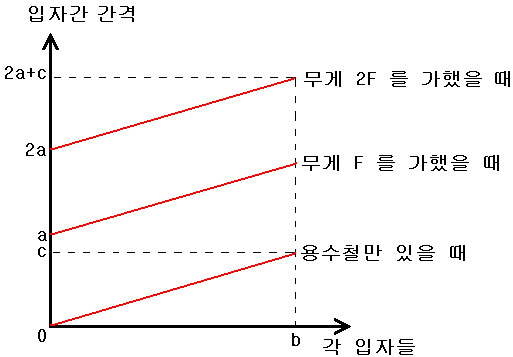
일단 아래 그림을 참조하죠.
용수철이 질량을 갖기 때문에 위쪽 용수철 입자들이 더 큰 무게를 받아서(아래 부분의 용수철 무게가 추가됨). 더 많이 늘어날 것입니다.
(b지점에 있는 입자가 가장 위쪽 용수철 입자일 것입니다. 실제로는 입자라기 보다는 제일 위쪽의 맨처음 입자간격을 뜻함 - 그 입자간격 크기는 c임)
용수철이 총 늘어난 길이는 각 입자들의 간격을 모두 합한 것일 것이므로, 그래프의 아랫부분의 면적이 될 것입니다.
따라서 용수철만 있을 때의 용수철이 늘어난 길이는 (1/2)*c*b 가 될 것입니다.
하지만 이것은 원래 길이에 더해지고, 아무것도 매달리지 않은 상태이기 때문에 그냥 처음 용수철 길이에 포함되어 있게 됩니다.
따라서 원래 길이에다 이 늘어난 길이를 합한 길이를 원래 길이로 치고, 이 때의 변위는 0 으로 치겠습니다.
이제 무게 F를 매달았을 때, 용수철이 늘어난 길이는 변위 0 으로부터 늘어난 길이로서,
위의 그래프에서 무게 F를 가했을 때의 그래프 밑 면적에서 용수철만 있을 때의 그래프 밑 면적을 뺀 것이 될 것입니다.
그 값은 계산하면 a*b 가 되겠지요.
그리고 무게 2F를 매달았을 때, 용수철이 늘어난 길이는 2a*b 가 됩니다.
즉, 무게 2F를 매달았을 때 늘어난 길이는 무게 F를 매달았을 때 늘어난 길이의 2배가 되는 것입니다.
쿨롱의 법칙 F = k*x 에서 k = F/x 가 됩니다.
위의 두 경우에서 위의 식에 대입해 보면, k가 둘 다 동일하게 나옴을 알 수 있습니다.
즉, 용수철이 질량이 있더라도 용수철 상수는 일정하다는 것입니다.
단, 실제 용수철에서는 용수철이 나선모양으로 구부러져 있어서 나선모양일 때의 탄성력의 함수가 어떻게 변할지가 관여되지만,
그냥 일반화 했을 경우, 용수철 상수는 용수철의 질량에 영향을 받지 않음을 짐작할 수 있습니다.