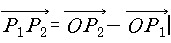전자기학 숙제 #2에 보면 이런문제가 있습니다.
1. P1 (-3,-4,5) 에서 P2 (2,0,-1) 로 향하는 벡터를
(a) 직각좌표계에서 표현하라
(b) 원통좌표계에서 표현하라
여기서 (a) 풀이시에 직각좌표계로 표현했을때
이걸 이용해서 (2+3)a^x+4a^y-6a^z의 벡터로 표현할 수 있다고 알고있습니다.
근데 이걸 그래프 상에서 나타내면
실질적으로 P1P2벡터의 위치와 직각좌표계로 표현한 5a^x+4a^y-6a^z의 위치가 같다곤 할 수 없는 것 아닌가요?
벡터가 스칼라값과 방향을 가지고 나타내는 것이라 두 벡터는 분명 같은 크기와 방향을 가진 벡터이지만
P1P2벡터는 실제로 P1좌표에서 P2좌표까지의 벡터인 반면 5a^x+4a^y-6a^z는 그 벡터의 위치벡터값과 같은
그러니까 원점에서 P1P2벡터와 크기 및 방향이 같은 벡터로 표시된 것으로 생각해도 무방한것 아닌가요?
직각좌표계상에서는 실질적으로 직각좌표계에서 표현된 벡터는 무조건 위치벡터로 표현된것이라 생각해도 되나요?
만약 그렇게 생각했을때에
(b)를 풀이할때 단순히 (a)번의 벡터 5a^x+4a^y-6a^z를 이용해서
P1에서 P2로 가는 벡터를 원점에서 (5,4,-6)까지의 위치벡터를 가지고 변환을 해서
Ara^r+Aza^z꼴의 위치벡터형태로 나타내도 무방한것 아닌가요?
제가 이 문제를 사실 이해를 잘 못해서 같은수업듣는 한정열에게 물어봤었는데
그 친구 말로는 P1점을 원통좌표계로 변환해서 그 좌표를 가지고 행렬식에 넣어서
그 좌표를 중심으로 원통벡터를 표현해야 됀다고 했는데
실질적으로는 벡터는 크기의 방향이 같으면 수학적으론 같은 벡터라고 생각해도 되기 때문에 두 벡터는 같은 벡터 아닌가요?
오늘 정열이가 이 부분에 대해 교수님께 여쭤봤다고했는데
같은 벡터라 할지라도 실제 과학적으로 벡터를 응용할떄 같은 크기와 같은 방향일지라도
예를들어 연필을 같은 크기와 같은 방향으로 밀때 연필 왼쪽에서 밀때와 오른쪽에서 밀때의 연필의 위치 라는 결과가 다르듯이
벡터의 시작위치가 다르면 다른 결과가 나올 수도 있기 때문에 다른걸로 간주해야된다고 하셨다고 들었는데
(스쳐 지나가면서 간략히 얘기 들은 것이라 제가 잘못 들었을 수도 있습니다)
처음에 이 말을 들었을때 원통 좌표계 내에서는 그럴수도 있겠다고 이해가 갔는데
직교좌표계에서는 P1P2를 표현한것이 위치벡터로 표현한것과 같은 모양 아닌가요?
만약 원통좌표계에서 두 벡터를 다르게 생각해야 돼는 이유가 실제 과학에서는 다른 결과를 나타내기 떄문이라면
직교좌표계에서는 그러한 차이점을 어떤식으로 두는것인지도 궁금합니다.
교재 28page 예제 2-5 (c)번 문제 처럼
원점에서 그 벡터의 수직거리를 따로 표현하거나
벡터 옆에 시작점의 좌표를 적거나 하는식으로 해야 돼는 것 아닌가요?
왜 직교좌표계에서는 따로 구분을 안짓는데
다른 좌표계에서는 위치벡터와, 다르게 표현하는 벡터의 두 벡터가 다른것으로 구분해서 생각해야되는지도 궁금합니다.
제가 저번에 올렸던 첫질문에서는 교수님께서
위치벡터에서는 원통으로 변환하였을때에 a^파이가 사라진다고하셨는데 일반적인 벡터에서 x,y,z 성분이 꼭 x, y, z 일 필요가 없으니
그런 일이 발생하지 않는다고하셨습니다.
근데 그런 벡터를 제외하고 일반적으로 좌표를 통해 구해진 직교좌표계의 벡터로 생각을 할 경우에는 아직도 이런 저런 궁금한점이 많이 남네요
그리고 (b)번을 원래 제가 풀던 방식처럼 직교좌표계상에서만 생각해서 위치벡터로 표현하면 틀린 풀이가 되는 것인지도 궁금합니다.