분산분석 - Oneway Anova(일원,일변량) - SPSS사용

[통계사랑]

분산분석은 여러가지 종류가 있습니다.

일원, 이원이 가장 많이 쓰이는 분산분석의 종류이며,

덧붙여 반복측정 분산분석이 있고, 이와 비슷한 공분산분석이 있습니다.

먼저, 분산분석을 왜 하는지를 아셔야 합니다

분산분석의 경우, 집단이 3개이상의 범주형 변수에 대한 연속형 변수의 값의 차이를 확인하고자 하는 분석입니다.

즉, 집단이 두개이면 T-검정을 하면 됩니다.

다시 말씀드려, 비교집단이 2개는 T, 3개 이상은 분산분석으로 이해하시면 됩니다

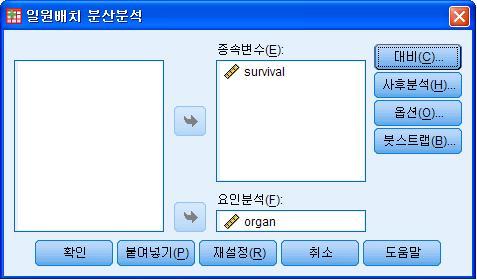
종속변수는 연속형 변수여야 하고, 독립변수는 범주형 변수여야 합니다.

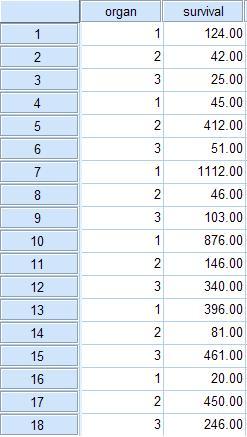
아래와 같이 데이터를 입력하시면 됩니다. 순서는 연속형이 먼저건, 범주형이 먼저건 상관없습니다. 다만, 확실히 무엇이 종속변수가 되고, 독립변수가 되는지를 확인하셔야 합니다. 단, 설문이 아닌 경우, 단순히 아래의 두가지 내용을 확인하고자 하는 것이라면, 반드시 범주형 먼저 입력을 해야 합니다.

아래의 데이터는 http://lib.stat.cmu.edu/DASL/에서 나온 데이터를 기본으로 합니다. 물론 약간의 수정은 있습니다만,

이는 보여드리기 위한 것이고, 데이터를 수정하는 것은 올바른 분석자의 자세가 아닙니다.

데이터를 설명하자면,

survival은 산 날짜(day)에 대한 것이고, organ은 해당 기관(부위)의 암에 관한 이름입니다.

즉, 해당 기관에 따라서 생명을 유지한 날이 같은지 다른지를 확인해 보고자 하는 것입니다.

귀무가설(H_0) : 해당 기관에 따른 생명유지 일 수는 차이가 없다.

대립가설(H_1) : 해당 기관에 따른 생명유지 일 수는 차이가 있다.

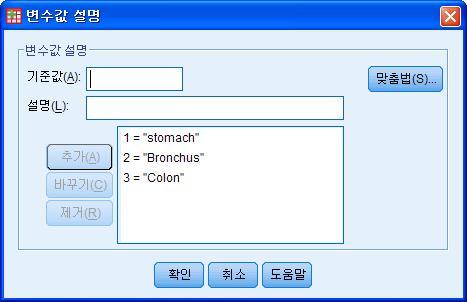
위의 그룹을 1,2,3으로 구분하였지만, 이는 변수값 설명에서 다음과 같이 바꿔서 사용하면 보다 쉽게 표를 사용할 수 있습니다.

분석>평균비교>일원배치 분산분석

사후분석옵션의 경우, 보통 많이 사용하는 방법이 Tukey, Dunacn, Scheffe의 방법입니다.

사후분석이란, 범주형으로 구분된 각 집단들끼리의 집단간 평균이 차이가 있다면, 각 집단별 차이가 어떻게 나는지

확인을 하기 위한 것입니다.

유의수준도 마찬가지로 임의로 선택가능하지만, 가장 많이 사용하는 0.05와 0.1이 있으니 확인하시고 사용하시면 됩니다.

옵션을 선택하고, 기술통계와 분산 동질성 검정을 눌렀습니다.  분산 동질성 검정은 levene의 통계량을 사용해서 검정하게 됩니다. 자세한 내용은 질문 해주세요.

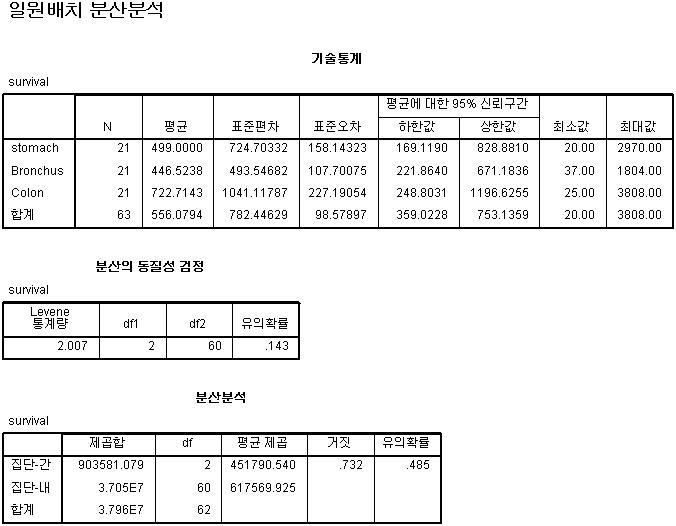
결과는 아래와 같이 나타납니다.

분산의 동질성 검정결과를 살펴보면, 귀무가설은 분산이 같다. 대립가설은 분산이 다르다. 입니다.

따라서 유의수준 0.05보다 크기때문에 분산의 동질성 검정결과 귀무가설을 채택할 수 있다고 보이며,

분산분석 결과를 살펴보면, 그룹별 차이가 없다고 할 수 있습니다.

물론, 차이가 평균을 확인하면 나타나지만, 이는 통계적인 의미에서 차이가 없다고 할 수 있습니다.

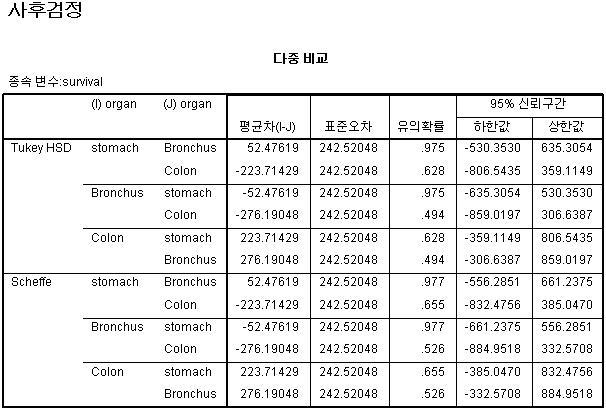
다중비교는 일반적으로 T-test를 여러번 한 결과와 같습니다. 즉, 각 집단을 두 개씩 구분해서 검정한 것으로

이해하시면 됩니다. 따라서 기준으로 하는 유의수준 보다 작다면 이는 두 집단간의 차이를 확인해 볼 수 있다는 뜻입니다.

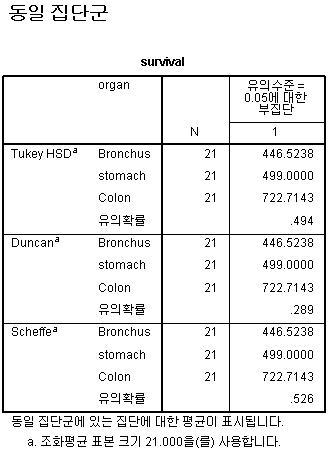
맨밑에 동일집단군의 경우, 집단의 크기가 같은 상태에서 비교하는 것입니다.

물론 많은 표본이 각 그룹마다 있으며, 전체 표본의 크기가 크면 무시할 수 도 있습니다.

자세한 내용은 질문해 주세요.

동일 집단군에 대한 내용을 확인해 보면, 세 그룹으로 구분한 범주형 변수는 차이가 없는 것을 확인해 볼 수 있습니다.

※ 중요한 것은 분산분석 결과 차이가 없다 하더라도, 그 이유를 연구자가 기술하고 이를 이용할 수 있다는 것입니다.

무조건적으로 차이가 나야하고, 그 결과가 달라야 한다는 가정은 연구를 제한적으로 만드는 것입니다.

차이가 나지 않는다면, 문제점 혹은 현황에 대한 이해를 다각도에서 생각해 볼 수 있으며, 충분히 논문으로

사용가능한 것입니다.

오늘도 화이팅입니다!!! 

[통계사랑]

유의확률과 유의수준으로 판단을 해야 합니다.

[우먼파워]

다변량분산분석의 예도 부탁드립니다.

[지영습]

Error : Sub Main has not been defined.
At Line No : 1
이러한 메시지가 뜨는데 무엇이 잘못된 건가요?

[사랑나들이]

고맙습니다. 유용하게 활용하겠습니다^^

[김기성]

동일 집단군에서 표본의 크기가 크면 무시해도 된다고 하셨는데 각 그룹마다 어느정도 수치의 표본이 있어야 무시할수 있죠?