빅뱅(9) 케플러 3대법칙

[남태근]

9. 요하네스 케플러의 3대법칙
   케플러는 티코 브라헤가 기록해둔 방대한 양의 관측자료를 분석 연구함으로서, 에라토스테네스 이후 천문학사에 길이 남을 업적을 발표하였다.

에라토스테네스가 지구크기를 계산한 이후 1800년이 훌쩍 넘는 시간이 지났다.
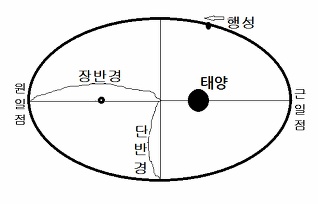
그는  “모든 행성은 태양을 하나의 초점으로 하는 타원궤도를 따라 공전한다”고 했다.

이른바 케플러 제1법칙(타원궤도의 법칙)이다.
최초로 태양중심설을 주장한 코페르니쿠스의 원운동의 오류를 바로 잡은 것이다.
케플러는 행성궤도의 신비를 알아낸 후 “ 오 하느님 제가 당신 다음으로 당신이 했던 생각을 해냈습니다.”라고 소리 질렀다.
  또, 행성이 타원궤도로 공전하기 때문에

태양(초점)으로부터 멀리 떨어져 있을 때(원일점)는 그 공전속도가 느려지고,

태양(초점)으로부터 가까이 있을 때(근일점)는 공전속도가 빨라진다.

즉, “같은 시간동안 태양과 행성을 직선으로 연결한 가상의 선이 휩쓸고 지나간 면적은 같다”는 것을 알아냈다. 이를 케플러 제2법칙(면적속도 일정의 법칙)이라 한다.
    마지막으로 ‘행성의 공전주기의 제곱은 공전궤도 장반경의 세제곱과 비례한다.

’케플러 제3법칙(조화의 법칙)‘이다.

제3법칙을 공전주기의 법칙이나 공전궤도의 법칙이라 칭하지 않고, 엉뚱하게 조화의 법칙이라 이름 지은 것은, 조물주가 세상을 창조하실 때 참으로 조화롭게 만드셨다고, 조화의 법칙을 이름으로 하였다고 한다,

주기는 물체가 원래위치로 되돌아오는데 걸리는 시간을 말한하고, 지구의 공전주기는 1년이 된다.

⟪ 건너뛰기 ⟫
케플러 제1법칙- 타원궤도의 법칙
   모든 행성은 태양을 하나의 초점으로 하는 타원궤도를 따라 돈다.

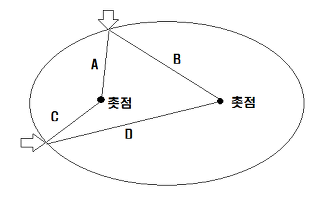
                    타원궤도                                                타원작도법
                              
타원을 그리는 방법은 두 초점에 실의 끝을 고정하고, 연필 끝으로 실을 팽팽히  당기면서 한바퀴 돌리면 타원이 된다.            A+B=C+D   (두 초점까지 길이의 합이 같은 점의 집합이다)

케플러 제2법칙- 면적속도 일정의 법칙
              

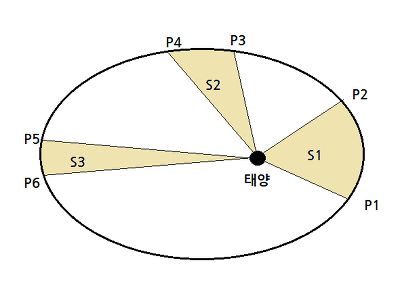
위 그림의 노란부분은 지구가 30일(일정기간) 동안 공전한 부분이다.
같은 기간 동안 공전하였다면 S1과 S2와 S3는 그 면적이 모두 같다.
따라서 공전속도는 P1~P2사이가 가장 빠르며, P5~P6사이가 가장 느리다.

케플러 제3법칙- 조화의 법칙
행성의 공전주기의 제곱은 공전궤도 장반경의 세제곱에 비례한다.
행성이 태양으로부터 멀어질수록 공전주기는 길어진다.
그것도 아름답고 조화롭게
                               𝐏²  =  𝐚³
                  주기의 제곱 = 장반경의 세제곱

즉, 지구보다 태양으로 부터 4배 먼 곳을 돌고 있는 행성이 있다면, 그 행성의 공전주기는 8년이 된다
목성의 장반경은 지구의 약 5.2배 이며, 공전주기는 약 11.86년이며,
토성은 장반경이 약 9.5 A.U 이며, 공전주기는 약 29.5 년이다.
1A.U = 태양에서 지구까지의 거리이며, 빛의 속력으로 환산하면 약 8분19초 거리이다.

[권순주]

타원궤도 때문에 사계절이 생기는 게 되고 다양한 생물이 번성할 수 있는계기가 된것이 아닐까요?

[남태근]

북반구에서는 지구가 태양의 근일점에 있을때 겨울이죠.
물론 이때 남반구에서는 여름이 되지만요
타원궤도이긴 하지만 이심률이 그리 크지 않으니, 태양으로부터의 거리가 미치는 영향은 크지 않으리라 봅니다

[권순주]

원형궤도 었다면 지구에는 지금과 같은 다양한 기후변화들과 지역들이 생기지는 않았을것 같아서요.
단순한 환경보다는 복잡한 환경이 생물의 다양성을 만들지 않았을까 추측해 봤습니다.^^

[남태근]

네
다양한 환경이 생물의 다양성을 더 할수 있겠네요! ^^