플랑크(Karl Marks Planck) 와 아인슈타인(Albert Einstein)은 공동으로, 식 E = hν 을 궤도전자의 진동에너지 또는 양자화된 전자파의 에너지를 표현하는 식으로서 제안했다. 그런데 식 E = kq^2m = m(2πνqm)^2 (5-1-4) 를 고쳐 쓰면,
E = (4π^2mνqm^2)ν (5-5-1)
∴ h = 4π^2mνqm^2Js (5-5-2)
가 된다. 이 식은 플랑크-아인슈타인의 식, E = hν 의 형식임을 알 수 있다. 즉, 식 (5-5-1)에, ν = cν0, ν0 = 109,737cm^-1(리드베리 주파수), 수소원자의 이온화 에너지 2.18 × 10^18를 대입하면, qm은 0.748Å 따라서 식 k = m(2πν)^2(5-1-3)에서, k = 389.336 kg/sec^2을 얻고, 한편 리드베리 주파수에 해당되는 파장은 λ0 = 911.26Å 이므로, 식 4qm/νa = λ/c, 또는 λ = 4qmc/νa(5-3-1)에서 νa를 구하면, νa = 984.2km/sec를 얻는다. 즉, 궤도전자고리가 이 속도로서 0.748Å의 진폭으로 세차진동 할 때 파장 911.25Å의 전자파를 발진한다. 그러나 궤도전자의 이 느린 속도는 영속전류의 전자의 운항속도가 아니라 전류 고리의 세차진동속도라는 것을 상기해야한다.(여기서 운항속도는 빛의 속도이다.) 보충설명을 하자면 원자수준의 미시세계에서 원자들이 전자파를 발진하는 기구를 설명하는 난점중의 두번째인 궤도전자의 거대한 운항주기와 발진되는 전자파의 주파수와를 서로 연계시킬수가 없었다는점.
한편, 플랑크 상수 h는, 식 (5-5-2)에 의하여, h = 6.6261…×10^34 Js로서 전통적인 값이 산출됨을 알수 있으므로 고전물리학 관점에서 보면, 여러종류의 물리적 인자가 그 속에 내포되어 있는 상수일수 없는 상수임을 알 수 있다. 즉, 식 중에서 특히 ν 는 상수로 고정할 수 없는 것이므로, E = hν로 일반화할 수 없다는 것도 알수있다.
ν가 상수로 고정할수 없는것이라고 했는데 저는 이부분이 이해가 잘안가네요. 어찌되었든 결론에는 동의할수 있을 것 같습니다. 플랑크 상수 내포되어있는 인자를 보았을때 말이죠. 결국 플랑크-아인슈타인의 식은 틀렸다는 겁니다.
이것을 확인하기 위하여 관계식 (5-3-1) 을 통하여 예시된 파장을 구하여 보았구여 다행히도 맞게나오더라구요. 그리구 나서 다시 세차진폭을 식(5-5-1)와 식(5-1-4)에서 대입하여 계산해보려고 시도하였는데 엄청난 자릿수때문인지 답을 구하지 못했네요. 한번 구해보시구요 값이 들어맞는지 알려주실분이 계셨으면 하네요. 오늘은 이만 마치겠습니다. 안녕히계세요.
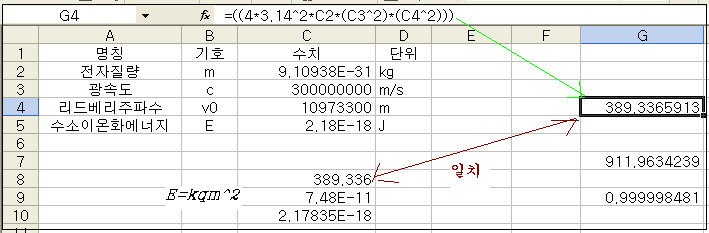
(5-1-3)식과 (5-1-4)식을 계산해서 일치를 확인함. 포기할 상황까지 갔었는데 k값의 소숫점이 책에 잘못 찍혀있는바람에 해맸네요^^;