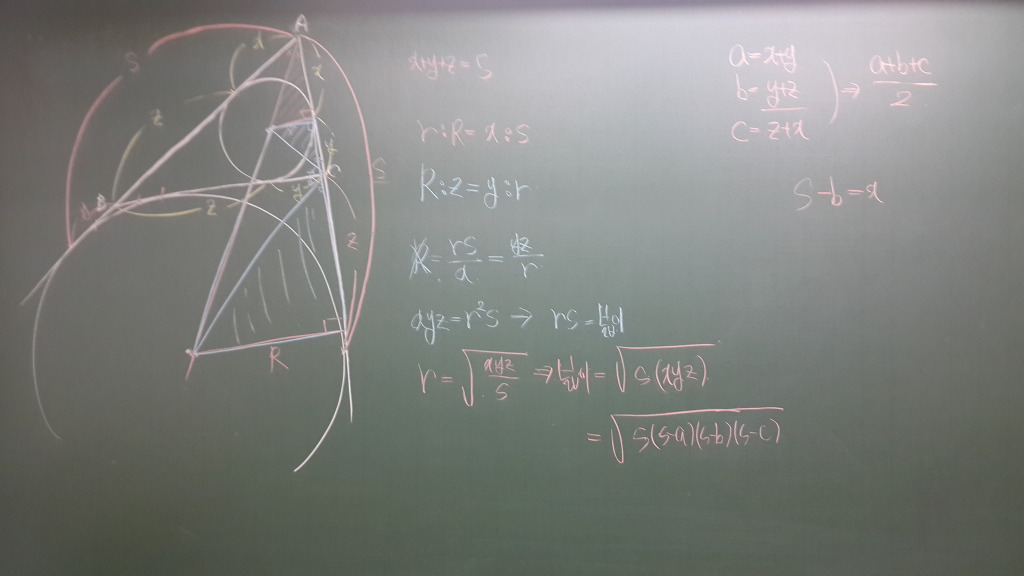올려봅니다. 많이 생략해서 필요한 부분을 간략히 적어봅니다.
1. 점A와 방심과 내심은 일직선 위에 있다.(이등분선이니까)
2. 파랑색 두 삼각형 사이의 각이 수직이다.
3. 두 파랑색 삼각형이 닮음이다.
4. 삼각형의 넓이 S = 0.5 * 내접원 반지름 * 둘레의길이
이것들을 종합하여 내접원의 반지름을 구할 수 있고 헤론의 공식으로 확장이 가능합니다.
다음검색
댓글
댓글 리스트-
작성자119man 작성시간 15.09.25 타원과 쌍곡선으로 증명한 것도 있어요.
-
답댓글 작성자송성근 작성자 본인 여부 작성자 작성시간 15.09.25 올려주세요
-
답댓글 작성자119man 작성시간 15.09.30 송성근 http://cafe.daum.net/beautifulmath/2rSf/1209?svc=cafeapp 타원과 쌍곡선이 접선과 두초점사이의 거리곱이 b^2가 생략되어 있습니다.
-
작성자뷰티플마인드 작성시간 15.09.29 굿좝~!