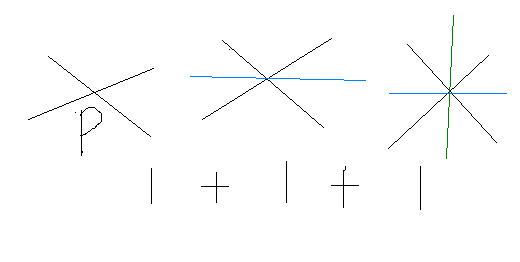평면위에 n개의 서로 다른 직선이 있다. 평면 분할에 의한, 분할면의 최대 개수는?
직선에 1,2,3,...,n의 번호를 부여한다. 번호 순서대로, 평면에 직선을 차례로 그린다
직선 1에 의해, 1 + 1 개 = 원래 평면 (1개) + 직선 1 (1개) = a_1
직선 2에 의해, a_1 + 1 + 1 = a_1 + 직선 2 (1개) + 직선1,2 의 교점 (1개) = a_2
우리는 분할면의 최대 개수를 구하고 있다
직선 k에 의해, a_1 + a_2 + ... + a_k-1 + 직선 k (1개) + 직선 k,1의 교점 (1개) +
... + 직선 k,k-1의 교점 (1개) = a_k 가 가능하고, 이것이 최대수라고 하면
직선 k+1에 의해 가능한 최대수는 무엇이며, 과연 그 최대수가 가능한가? 를 알아보자
1) 가능한 최대수는?
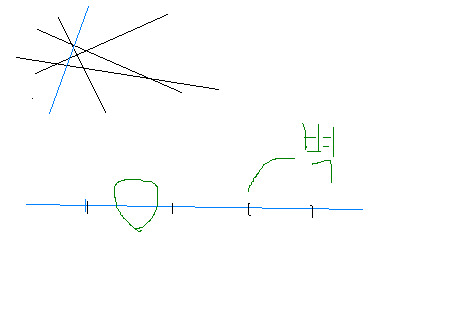
파란 직선은 새로 그려지는 직선인데, 위의 검은 표시 4개는, 다른 기존 직선과의 교점들이다
이 교점이 벽과 같은 역할을 한다. 원래 파란 직선은 없었다. 그런데, 파란 직선이 그려져서
녹색 동그라미 부분에서 보듯이, 벽과 벽 사이에서, 새로운 분할면이 1개 생기게 된다
이런식으로 보면, 벽의 총개수 (교점의 총개수) + 1개 (파란 직선) 이, 새로 생기는 분할면의
개수이다. 벽이 하나 없으면 손해다. 즉, 어떤 두 직선도 평행하면 손해다
또, 벽이 겹쳐도 손해다 (교점이 겹치면 손해) 즉, 어떤 세 직선도 한점에서 만나면 손해다
그레서, 직선 k+1은, 기존의 모든 직선과 교점(벽)을 형성해야 한다
a1 + a_2 + ... + a_k + 1 + k = a_k+1
2) 이것이 항상 가능한가? ( 그러한 파란 직선을 항상 그릴 수 있나? )
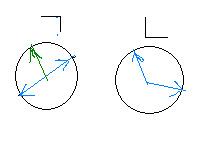
좌표평면에서,직선들의 단위 법선벡터 (이하 법선벡터로 표기함)를 생각하면, 하나의 직선에 2개가 있다
모든 단위 법선벡터들은, 좌표평면에서 종점이 단위원 위에 있게 된다
두 법선벡터의 종점이 단위원의 지름에 놓이면, 해당 두 직선은 평행하며 ... (ㄱ)
두 법선벡터의 종점이 단위원의 지름에 놓이지 않으면, 해당 두 직선은 한 점에서 만난다 ... (ㄴ)
(녹색은 두 벡터가 겹친 것임)
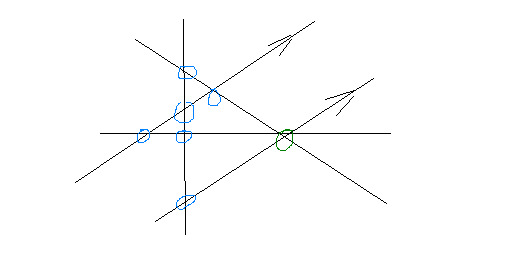
k개의 직선에 대한, 법선벡터 k개가, 분할면의 개수가 최대인 조건을 만족하며 놓여있다고 하자
직선 k+1의 법선벡터는, k개의 법선벡터들과 지름만 형성안하게 놓이면 된다
이는 무한가지로 가능
그리고 k개의 직선들에 의해 생기는, 교점의 개수는 유한개이다
직선 k+1의 법선벡터의 방향은 위와 같이 하면 되고, 직선 k+1이 유한개의 교점만 피하게 그리면 됨
이런식으로, 귀납적으로, 항상 최대값이 가능하게, 직선들을 순차적으로 그릴 수 있다
따라서 1(원래 평면) + n (n개의 직선) + nC2 (가능한 모든 교점의 개수)
= nC0 + nC1 + nC2 개가 우리가 구하는 최대값이다
............................................................................................................................
위의 문제에서 주의할 점은
1) 직선이 순차적으로 첨가되어 그려짐에 따라,
생기는 선(직선), 교점 은 유일하다는 것이다
n개의 서로 다른 직선이니, 선이 겹칠리는 없고, 교점도 겹치지 않는 경우가 (어떠한 세 직선도 한점에서 먼나지 않는다) 위에서 구한, 분할면의 최대값이다
2) 분할면의 개수가 최대값을 갖는 그림을 그렸다고 하자,
이 그림에서, 직선이 순차적으로 그려지는 방법의 수는 n! 가지이다
이 각각의 모든 경우에서, 분할면의 최대값은 불변이다
거꾸로 하나씩 직선들을 제거해 보면 알 수 있다 ( 직선 n제거,직선 n - 1 제거, ... )
왜 불변인가? - 교점도 겹치지 않고, 선도 안 겹치므로
.................................................................................................................................
교점이 겹치면 어떻게 되는가?
- 겹치는 것은 여러번 카운팅된다 - 이것을 알아야 한다
평면에서 분할면의 개수를 세는데, 우리는 분할면을 일일이 세지 않는다
오직 선과 교점의 개수만 센다 ... 이래야 계산으로 구할 수 있으니까
그러면 그 계산 규칙을 찾아야 한다
예를 보자 ... 아래에서 분할면의 개수 = 14 개 ( 평행한 직선 한쌍, 한 교점에 세 직선 )
어떤 하나의 교점(선 or 평면)이 x개의 분할면을 만들때, 이 교점(선 or 평면)은 x당량 이라고 하자
m개의 직선이 한 교점에서 만날때, 이 교점의 당량은 m-1C1 이다 ( m ≥ 2 ) @@@
( 이 교점은 m-1C1 개의 분할면을 만든다는 것이다 )
각 직선은 1당량이며, 원래 평면도 1당량이다 ... 이렇게 일대일 대응을 시키는 것이다
따라서 위의 예의 분할면의 개수 = 1(원래 평면) + 5 (선 5개) + 6 (1C1) + 1 (2C1) = 14
1C1 ,2C1 은 당량임
...................................................................................................................................................................
설명: 변수는 2가지이다
1) 평행선들이 있는 경우 2) m개의 직선이 한 교점 P 에서 만나는 경우
1)의 경우는 계산하면 되므로, 2)만 보자
m개의 직선 중, 어떤 두 직선의 법선벡터의 종점도, 단위원의 지름에 놓이지 않으므로,
어느 순간, 또 어느 순간 직선을 하나씩 제거해도, 위의 상태는 불변이다
( m -1개의 직선이 한 교점에서 만남, m - 2 개의 직선이 한 교점에서 만남 ... )
원래 평면에 직선을 하나씩 차례로 그릴때, k번째 직선이 그려져서, 다른 직선과 만나,
처음으로 교점 P가 생긴다 ... 이때 P로 인해, 하나의 분할면이 생긴다
어느 순간 k + 20 번째 직선이 그려지는데, 이 직선이 P를 지난다 ...
이때도 P로 인해, 하나의 분할면이 생긴다
또, 어느 순간 k + 100 번째 직선이 그려지는데, 이 직선이 P를 지난다 ...
이때도 P로 인해, 하나의 분할면이 생긴다
이런 식으로 m-1C1 당량 이 설명된다
이는 직선이 순차적으로 그려짐에 따라 생기는, 자연스러운 결과이다
평면에서는 항상 그려지는 직선의 순서를 임의로 바꿔도, 분할면의 개수를 계산하는 과정에서 변화가 없고, 그 결과 또한 동일하다 ( 거꾸로 직선을 임의의 순서로, 하나씩 제거해 보면 알 수 있다 )
결국 평면 분할은 어떤 경우든, 계산식으로 분할면의 개수를 구할 수 있다
위의 예에서, 서로 다른 5개의 직선 (한 쌍의 평행선) , 세 직선이 하나의 교점 형성 이므로
원래 평면 : 5C0 , 직선 : 5C1 , 교점 : (5C2 - 2C2 - 3C2) (1C1) + 1 (2C1) ... 1C1, 2C1 은 당량임
모두 더하면 14 = 분할면의 개수
.............................................................................................................................
공간에서 세 평면의 위치관계와 이들 평면의 (단위) 법선벡터와의 관계를 알아 보자
... (단위) 는 생략해서 적음
공간에서 평면의 모든 법선벡터는, 그 종점이 단위구 위에 놓인다
( 단위구의 중심이 원의 중심이 되는 원을 대원이라 하며, 대원은 단위구의 중심을 지나는 평면이
단위구면과 만나서 생기는 교선이다 )
법선벡터의 종점인, 단위구면 위의 점에서의 접평면이, 해당 평면과 평행임을 생각하자
1) 세 평면의 법선벡터의 종점이, 대원위에 놓이는 경우
- 이 경우, 대원위의 종점에서의 (단위구의) 접평면들을 생각하자
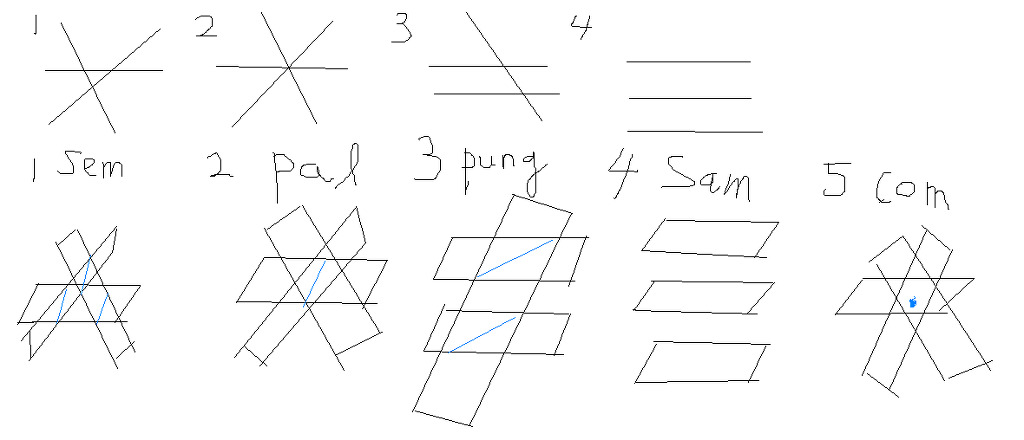
이것은 마치 평면위의 세 직선의 위치관계와 동일한 패턴임을 알 수 있는데, 다음과 같다
1,2,3,4 까지만 나오며, 위,아래 그림을 보면 알 수 있듯이 매우 유사하다
이것은 대원위의 종점에서의 단위구의 접평면들을 생각해 보면, 당연한 그림이다
1. sem 상태 ( 제 눈에 세모(sem)같이 보여서 ) ... 파란색 세 교선이 평행하다
2. pal 상태 ( 팔랑(pal)개비 같이 생겨서 ) ... 파란색 하나의 공통 교선
3. pung 상태 ( 평(pung)행해서 ) ... 파란색 두 교선이 평행하다
4. sam 상태 ( 한자 석삼(sam)자 같이 생겨서 )
2) 세 평면의 법선벡터의 종점이, 대원위에 놓이지 않는 경우
... 위의 5번 상태로 ( com 상태 (common) ... 일상적인 상태라서 )
세 평면이 하나의 파란색 교점에서 만난다
com 상태는 어떻게 알 수 있는가 하면, 일단 두 법선벡터가 0도,180도의 각은 못 이루니까
( 만약 0도,180도면, 나머지 법선벡터의 위치에 관계없이, 무조건 대원위에 세 법선벡터의 종점이 놓임 )
두 평면이 우선 만나 교선이 생기고, 남은 하나의 평면과 이 교선과의 위치 관계를 따지면 되는데,
( 하나의 평면과 하나의 직선의 위치관계가 됨 )
남은 하나의 평면과 교선이, 한점에서 만나는 경우만 남게 된다
< 용어 정의 > m ≥ 3
공간에서 m개의 평면에서의 pal 상태 : m개의 평면이 하나의 교선을 지나는 경우
공간에서 m개의 평면에서의 com 상태 : m개의 평면이 하나의 교점에서 만나는 경우로
어떠한 3개의 평면도, 위 그림의 com 상태인 경우
....................................................................................................................
설명에 한계가 있습니다. 공간 상태는 그림그리기에 한계가 있어서 당장 이해가
안 될 수 있지만, 중요한 것들은 모두 적으려고 합니다