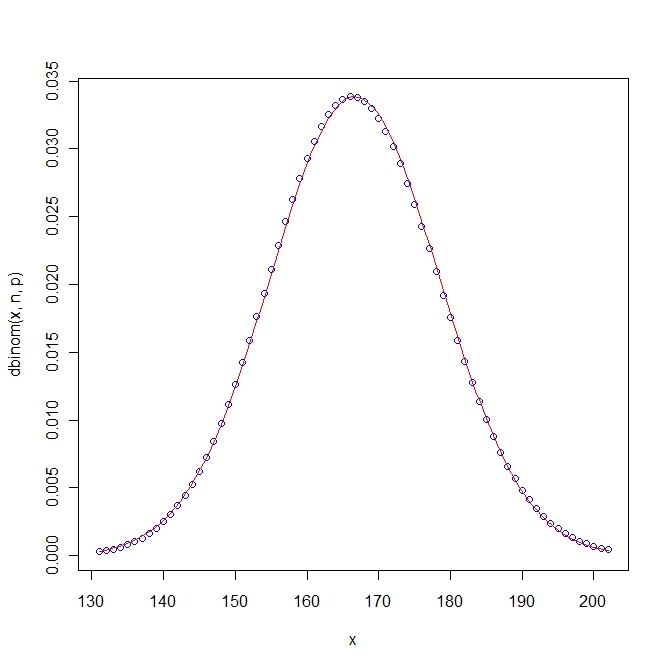
주사위를 1000번 던졌을때 6의 눈의 수를 x라고 했을때, x의 분포를 이항분포와, 정규분포 근사로 그려보자.
n=1000; p=1/6
# 이항분포의 평균, 표준편차는 이렇게 구하죠. 학부 기초 통계학에 나옵니다.
mu=n*p; sigma=sqrt(n*p*(1-p))
# x의 범위를 +- 3*sigma로 하면(넓힐 수도 있겠죠) c(-1,1)을 +- 입니다.
> mu+c(-1,1)*3*sigma
[1] 131.3113 202.0220
x=131:202
# 이항분포(점선)
plot(dbinom(x,n,p)~x, col="red")
# 정규분포(실선)를 덧그리면
curve(dnorm(x,mean=mu,sd=sigma),add=TRUE, col="blue")
거의 일치하죠. p=1/6같이 0이나 1에 너무 가깝지 않고 n이 1000정도로 크면 이항분포는 정규분포근사와 거의 일치합니다.
다음검색