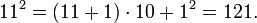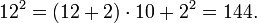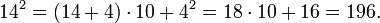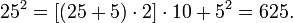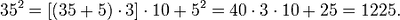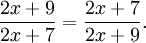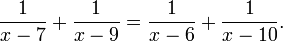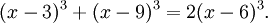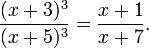수학의 태동은 천문학

[유토피아]

수학은 인류의 역사와 더불어 시작되었다고 할 만큼 오래되었다.

선사 시대의 유적 중에는 문자가 없던 이 시기에 이미 별을 이용하여 측량을 하는 수학적인 지식이 있었음을 보여주는 그림이 남아있다. 

2002년 고생물학자들은 남아프리카의 동굴에서 암석을 연구하다가 약 7만년 전에 기하학적인 무늬를 새긴 돌을 발견하였다.

] 또한 아프리카 35,000년 전에 제작된 것으로 추정되는 기초적인 셈이 표기된 유물을 발굴하기도 하였다.

선사시대의 유물 중에는 이상고 뼈와 같이 뼈나 돌에 28 - 30개의 줄을 새긴 것들이 있다.

이는 여성이 월경 주기를 계산하기 위해 표시한 것으로 보인다. 

또한 사냥꾼이 자신이 잡은 동물의 수를 표시하기 위해 금을 새긴 것으로 보이는 유물도 발견된다.[4]이상고 뼈는 1960년 콩고와 인접한 나일강 발원지 부근에서 발견되었다. 

2만년 전에 만들어진 것으로 추정되는 이 뼈에는 소수를 이용한 고대 이집트의 구구법과 같은 수열이 새겨져 있다.

기원전 5천년경 전왕조 시대의 이집트에서는 기하학을 이용하여 공간을 분할하기 시작하였다. 

한편, 기원전 3천년경 만들어진 잉글랜드와 스코틀랜드의 거석 구조물에는 원, 타원, 피타고라스 수와 같은 수학적 지식이 사용되었다.[5]

기원전 3000 ~ 2600년경 고대 인도의 인더스 문명에서는 십진법을 이용한 도량법이 만들어져 비율과 함께 벽돌 건축 기술에 사용되었다.

인더스 문명의 건축가들은 자, 컴파스와 같은 기하학 도구를 사용하여 자신들의 도시를 설계하였다. 

이로써 인더스 문명의 도시에는 직각으로 이루어진 도로가 놓이고 직육면체, 원기둥, 원뿔등이 적용된 건물이 들어섰다. 

인더스 문자가 아직 완전히 해독되지 않아 당시의 인도 수학은 일부만이 알려져 있다. 

고고학적 연구결과에 따르면 인더스 문명은 팔진법을 이용한 기수법을 사용하였고 고유의 π 값을 사용하였다.[6]

중국에서는 상나라 시기 거북 등에 그려진 그림과 같은 마방진이 알려져 있었다.

수학의 역사는 인류의 역사와 더불어 시작되었다고 할 만큼 오래 되었다. 

수학사(數學史)로 알려진 학문 분야는 본래 수학의 새로운 발견에 대한 기원을 탐구하는 것이며, 더 작게는, 과거의 표준적인 수학 방법과 용어에 대한 탐구이다.

교역 ·분배 ·과세 등 인류의 사회 생활에 필요한 모든 계산을 수학이 담당해 왔고, 농경생활에 필수적인 천문 관측과 달력의 제정, 토지의 측량 또한 수학이 직접적으로 관여한 분야이다. 고대 수학을 크게 발전시킨 나라로는 이집트, 인도, 그리스, 중국 등이 있다.

근대 이전 시대에는 지식의 전 세계적인 확산이 이루어지지 않았기 때문에 새로운 수학적 발전이 문자로 기록된 경우는 일부 지역에 국한된 것이었다. 현존하는 가장 오래된 수학적 텍스트들은 플림톤 322(바빌로니아 수학, 기원전 1900년경), 모스크바 수학 파피루스(이집트의 수학, 기원전 1850년경), 린드 수학 파피루스(이집트의 수학, 기원전 1650년경), 술바 수트라스(인도의 수학, 기원전 800년경) 정도이다. 이들 모두는 이른바 피타고라스의 정리라 불리는 것에 관한 것으로, 고대 시대에 이미 아주 오래전부터 기초적인 산술과 기하학적 지식으로 널리 알려져 있었다.

고대 이집트와 바빌로니아의 수학으로부터 발전한 고대 그리스와 헬레니즘 시대의 수학은 수학적 방법과 다루는 주제를 크게 확장시켰다. 

특히 엄격한 증명의 도입은 그리스 수학의 업적이다.

 [1] 이들 고대 문명에서 발전한 수학은 이슬람 수학에서 더 발전하고, 크게 확장되었다.

 12세기 무렵 그리스와 아랍의 수학 문헌들이 중세 유럽에서 라틴어로 번역되어 더욱 발전하였다.

고대와 중세 수학사의 인상적인 특징은 수학의 폭발적 발전이 종종 침체기 이후에 뒤따른 다는 것이다.

 16세기 르네상스 초기 이탈리아에서, 새로운 과학적 발견에 영향을 준 새로운 수학적 발전들이 빠른 속도로 이루어졌고,

이는 현재에도 계속되고 있다.

----------------------------------------------------------------

가장 원시적인 기수체계는 단항 기수법으로서, 단위 수를 수직선, 원, 또는 점 등의 기호를 반복하는 방식으로 숫자를 나타낸다. 예를 들어 만약 1을 나타내는 단위 기호가 |이라면 5는 |||||, 10은 ||||||||||로 표기한다. 초기의 단항 기수법에서는 숫자를 나타낼 때 단위 기호를 동일선 상에서 표기하였으나, 일직선의 기호들로 나타낸 숫자들은 사람들의 눈에 쉽게 들어오지 않았으며, 이에 따라 시간이 지나면서 한 줄에 있는 기호가 특정한 개수를 넘으면 다음 줄로 넘어가는 방식으로 숫자를 쓰기 시작했다. 학자들에 따르면 일렬로 나열된 단위 기호가 4개를 넘으면 쉽게 숫자를 인식하지 못하기 때문에 단항 기수법에서 한 줄에 존재하는 단위 기호는 최대 4개인 것이 일반적이라고 한다. 실제로 이집트 인이나 크레타 섬 주민들의 경우 초기 단항 기수법에서 한 줄에 단위 기호를 4개씩 표기하였으며, 바빌로니아 인이나 페니키아 인들도 3분 원칙을 채택하여 실제 고대 문명의 단항기수법에서도 4의 법칙을 확인할 수 있다.[1] 또한 어떤 문명은 아예 숫자 5에 대한 기호를 만들어 초기 단항 기수법에서 발생했던 숫자 인식의 어려움을 극복하고자 하였다.

------------------------------------------------------------------

바빌로니아 문명에서 기수법이 고안된 것은 함무라비 왕 직전이라고 전해지고 있으며, 비슷한 시기에 발전하였던 기수 체계들과 달리 위치적 기수법을 사용하였다. 바빌로니아 기수법은 오늘날 가장 널리 사용되는 10진법이 아닌 60진법을 토대로 하여 한 자리에 올 수 있는 계수(係數)는 1부터 59까지 총 59개였다. 또한 숫자의 자릿수는 60에 대한 계수()를 의미한다. 바빌로니아 기수 체계에서는 59개의 계수를 단위 수 1을 나타내는 '못 ' 모양의 문자와 10에 해당하는 '서까래' 두 가지 기호의 조합으로 나타내는데, 그 형태들이 못과 쐐기에서 따왔다고 하여 설형문자라고 말한다. 1부터 59까지의 수는 이 '못'과 '서까래'를 반복하여 표시하였다. 예를 들어 55는 못 5개와 서까래 5개로 표기하고 14는 못 4개의 서까래 1개로 나타낸다. 그러나 60을 넘어서면 위치값 기수법에 근거하여 두 자리 이상으로 수를 표시하였는데, 몇 가지 수를 바빌로니아식 기수법으로 나타내면 아래와 같다.

1.75: 바빌로니아식 표기 - (1;15)[못 1개 ; 서까래 1개와 못 1개]

2.1000: 바빌로니아식 표기 - (16;40)[서까래 1개와 못 6개 ; 서까래 4개]

3.400: 바빌로니아식 표기 - (6;40)[못 6개 ; 서까래 4개]

여기에서 바빌로니아 기수법은 위치적 기수 체계(60진법)를 기본 바탕으로 설형문자로 계수(係數)를 나타내는 과정에서 10개의 못을 서까래 1개로 나타내는 등의 부가적인 원칙을 채용한 복합적인 구조였음을 확인할 수 있다. 추가적으로, 아래의 기록에서도 바빌로니아 문명이 60진법을 사용했다는 것을 쉽게 확인할 수 있다.

바빌로니아 기수법의 한계바빌로니아 문명은 위치적 기수법을 사용하였지만, 오늘날 0의 역할처럼 특정한 위치가 수의 표현에서 의미가 없음을 나타내는 기호가 특별히 존재하지 않아 숫자 표기의 애매모호함을 피할 수 없었다. 예컨데 바빌로니아 기수법에 의하면 2는 (못 2개), 61은 (못 1개;못 1개)로 표시하지만, 두 숫자 모두 못 2개의 연속적인 배열로 표현되기 때문에 혼동을 일으킨다. 이런 문제점을 인식한 일부 바빌로니아의 서기들은 혼동을 피하고자 자릿수 사이의 띄어쓰기를 명확하게 하여 수를 표기하기도 하였지만, 종종 신중하지 못한 서기들이 띄어쓰기를 제대로 하지 못해 숫자 표기에서 모호함은 계속되었다. 이처럼 초기 바빌로니아 기수법의 근본적인 한계는 바로 '없음'을 나타내는 기호 자체가 없었다는 것이다. 하지만 현대 학자들은 바빌로니아 학자들이 그들의 애매한 위치적 기수 체계에 별다른 불편함을 느끼지 않았다고 생각하고 있으며, 이 체계는 바빌로니아 문명이 존재했던 오랜 시간동안 지속되었다.

바빌로니아 기수법에서 '없음'(특정 위치의 무의미성)의 기호가 나타난 것은 기원전 3세기 경으로, 이는 역사에서 가장 오래된 '없음'의 개념이다. 그러나 없다는 것을 의미하는 바빌로니아식 기호와 오늘날 우리가 사용하는 0의 의미에는 약간의 차이가 있다. 바빌로니아 사람들은 그들이 만든 '없음'의 기호를 양이 아무것도 없는 것을 표현하는 데 쓰지 않고 단지 특정 위치에서의 공백을 나타낼 때만 사용하였다. 현대적으로 표현하면, 0이라는 기호를 102, 4006 등 숫자를 표기하는 과정에서는 썼지만 30-30 이라는 연산에 대한 답으로서 0을 쓰지는 않았다는 것이다.(대신 "다 떨어졌다", "없어졌다" 등의 문장 표현을 사용했다고 한다.) 이처럼 바빌로니아 사람들은 위치에서의 공백과 양적으로 없는 것을 다루게 간주하였다. 비록 완전하지는 않지만, 바빌로니아의 기수 체계는 최초로 위치적 기수법을 도입하고 공백을 나타내는 기호를 처음으로 발명했다는 것에서 충분히 수학사적 가치를 가진다.

---------------------------------------------------------------------

고대 이집트의 10진법고대 이집트 문명에서 기수법이 고안된 것은 약 기원전 3000년부터라고 전해지고 있으며, 이 기수법은 기원후 1000년 초까지 고대 이집트에서 사용되어왔다. 고대 이집트 기수법은 현대인들이 주로 쓰는 10진법을 사용하였으며, 표기 방법으로는 명수법을 기초로 하고 있다. 10진법을 사용함에 따라 1, 10, 100, 1000 등의 숫자들을 특정한 기호로 표기하였는데, 이러한 기호들에는 모두 특정 사물을 본 따서 만든 상형문자가 사용되었다. 1은 막대기, 10은 발뒤꿈치 뼈, 100은 감아 놓은 밧줄, 1000은 연꽃 줄기, 10000은 손가락, 10만은 개구리 혹은 올챙이, 100만은 두 손을 위로 올린 사람 등의 모습으로부터 상형문자를 고안했는데, 기호 관념을 갖추고 있었던 이집트 문화 속에서 이들 기호가 어떤 신비주의적 중요성을 띄었던 것이라고 추측하는 이들도 있다. [3]예를 들어 100만의 경우, 당시 고대 이집트에서 100만이란 숫자는 어마어마하게 크고 거대한 수였기에 100만에서 느껴지는 경외감을 사람이 두 손을 위로 들어 신을 경배 하는듯한 모습으로 표현한 것이라고 할 수 있다는 것이다. 이러한 상형문자를 이용한 기수법은 자리마다 다른 기호가 필요하므로 모든 수를 표현하려면 상형문자 기호가 무한히 많아야 했겠지만, 실질적으로 고대 이집트에서 10만보다 큰 수가 필요한 경우는 드물었기에 이러한 기수법이 오랜 기간 유지되었던 것이다. 아래의 표는 고대 이집트에서 숫자에 사용된 상형문자를 정리한 것이다.

-------------------------------------------------------

중국 문명의 기수법중국의 숫자체계는 특정 숫자들을 발음할 때 쓰이던 중국의 문자들로 구성되어 있는데, 이 숫자 체계는 과거 한자 문화권에 포함되어있던 일본, 한국에서도 사용되었다. 이러한 숫자 체계는 영어처럼 발음에 쓰이던 문자들로 구성되어있기 때문에 아라비아 숫자 등에서 쓰이던 위치 기수법이 사용되지 않았다. 중국에서 숫자를 나타낼 때 쓰였던 문자들은 다음과 같이 크게 4가지로 나눌 수 있다; 상 왕조 시대의 숫자, 청동기 시대의 숫자, 막대 숫자(산가지), 표준 숫자.

[편집] 상 왕조 시대의 숫자

기원전 14세기의 상 왕조 시대 때 쓰였던 숫자상 왕조 시대 이후의 중국 숫자들은 대부분이 기원전 14세기인 상 왕조 시대 때 쓰이던 숫자에서부터 비롯되었다. 갑골 문자로 알려진 상 왕조 시대의 숫자는 거북이의 등껍질과 동물의 뼈에서 처음 발견이 되었다.

[편집] 청동기 시대의 숫자

서 저우 왕조에서 쓰였된 숫자청동기 시대의 숫자들 중 1, 2, 3, 4, 10, 11, 12, 13 등의 숫자들에 쓰이던 기호들이 이후의 중국 숫자인 막대 숫자(산가지)에도 그대로 쓰였다.

[편집] 산가지산가지는, 각 숫자들을 막대기로 표현하였는데, 혼란을 방지하기 위해 수직과 수평을 번갈아 가면서 사용하였다. 일반적으로, 수직 막대는 한 자리 수, 백의 자리 수, 만의 자리 수 등을 표현하는데 사용되었고, 수평 막대는 십의 자리 수, 천의 자리 수, 십만의 자리 수 등을 표현하는데 사용되었다. 산가지 숫자 체계는 16세기의 한나라 때부터 쓰였는데 주로 상인, 수학자, 천문학자들에 의해 사용되었다.

七 一 八 二 四

万 千 百 十 步

[편집] 표준 숫자중국의 표준 숫자는 크게 두 가지로 나뉜다. 일반적인 생활에서 쓰이는 숫자와 경제 관련 문서에서 쓰이는 숫자가 바로 그것이다. 경제 관련 문서에는 일반적인 생활에서 쓰이는 숫자와 다른 숫자를 썼는데, 그 이유는 일부 중국 숫자의 특성 상 획을 몇 개 추가하거나 수정하면 다른 수를 뜻하는 문자가 되어버리기 때문이다. 예를 들어, 三十(30)의 경우, 三에 두 획을 그으면 五, 十에 한 획을 그으면 千이 되어 三十(30)이 五千(5000)으로 바뀌어 버린다. 일반적인 생활에서는 이와같이 숫자를 바꿀 필요가 없지만, 경제 관련 문서에서는 위조가 될 가능성이 매우 높아지게 된다. 따라서, 중국 표준 숫자에서 경제 관련 문서에 쓰이는 숫자는 일상 생활에서 쓰이는 숫자에서 수정 가능한 숫자들을 몇 개 바꾼 것을 사용한다.

전 = 전통적인, 간 = 간이화된.

경제 관련 문서 일반적인 문서 크기 병음

零 〇 0 líng

壹 一 1 yī

貳 (전) 또는

贰 (간) 二 2 èr

叄 (전) 또는

叁 (간) 三 3 sān

肆 四 4 sì

伍 五 5 wǔ

陸 (전) 또는

陆 (간) 六 6 liù

柒 七 7 qī

捌 八 8 bā

玖 九 9 jiǔ

拾 十 10 shí

佰 百 100 bǎi

仟 千 1,000 qiān

萬 萬 (전) 또는

万 (간) 104 wàn

億 億 (전) 또는

亿 (간) 108 yì

중국의 일부 지역에서는 표준 숫자에서 일부분 바뀐 숫자들을 사용한다.

바뀐 숫자 크기 병음 표준 숫자

幺 1 yāo 一

兩(전) 또는

两(간) 2 liǎng 二

呀 10 yā 十

念(전) 또는

廿(간) 20 niàn 二十

卅 30 sà 三十

卌 40 xì 四十

皕 200 bì 二百

[편집] 그리스 문명의 기수법[편집] 그리스 숫자그리스 기수법은 그리스 문자를 사용하여 숫자들을 표현하는 방식이다. 고대 그리스에 알파벳이 만들어지기 전에 사용되던 숫자 체계를 '에게 숫자'라고 부르는데, 이 숫자 체계에는 1, 10, 100, 1000 그리고 10000에 해당하는 기호들이 존재하여 그 기호들의 조합으로 숫자를 표현하였다.

| = 1, – = 10, ◦ = 100, ¤ = 1000, ☼ = 10000

'에게 숫자' 이후 고대 그리스인들은 두 가지의 숫자 체계를 사용했는데, 둘 중 먼저 만들어진 것은 수를 순서대로 배열한 뒤 로마 숫자처럼 무리를 지어 사용하는 숫자 체계이었다. 이를 '열(列) 숫자' 혹은 '아티카 숫자'라고 부르는데, 이 숫자 체계에는 1, 10, 100, 1000 그리고 10000의 계수를 나타내는 개별적인 기호들이 존재한다. 또한, 위와 같이 10진법의 집단화를 나타내는 기호들 외에, 5에 의한 집단화를 나타내는 기호들도 존재하는데, 여기서 1을 제외한 나머지 계수들(10, 100, 1000, 10000)을 나타내는 기호들은 각 계수를 나타내는 수 단어의 첫 글자들이며, 5에 의한 집단화를 뜻하는 기호들은 5를 나타내는 수 단어 pente의 첫 글자인 <Π>를 사용하여 나타내어졌다. [4]

Ι = 1, Π = 5, Δ = 10, ΠΔ = 50, Η = 100, ΠΗ = 500, Χ = 1000, ΠΧ = 5000, Μ = 10000, ΠΜ = 50000

'열(列) 숫자' 혹은 '아티카 숫자'에 이어서 그리스에 알파벳으로 이루어지고 유사십진법을 사용하는 학문적인 숫자 체계가 등장하였는데, 바로 '이오니아 숫자'이다. 기원전 5세기에 처음으로 등장한 '이오니아 숫자'는 기원전 1세기부터 그리스의 도시 중 하나인 아테네의 공식 숫자 체계로 사용되었는데, 이 숫자 체계는 각 일의 자리(1, 2, ..., 9)와 십의 자리(10, 20, ..., 90), 백의 자리(100, 200, ..., 900)를 나타내기 위해 각각에 별도의 문자를 할당하였다. 여기에는 총 27개의 문자가 필요한데, 그리스 문자인 24자 이외에 지금은 쓰이지 않는 옛 문자인 디감마 ϝʹ 혹은 스티그마 ϛʹ(6), 코파 ϟʹ (90), 삼피 ϡʹ(900)이 사용되었다. [5]

  --------------------------------

이집트, 수의 기원 수는 어떻게 생겨났을까? 

- EBS 다큐프라임 모든 문명에 숨겨진 비밀, 수와 기하 ‘문명과 수학’

프로그램 모니터링 / EBS스토리 기자단

2011/12/26 08:50

http://ebsstory.blog.me/50129736997

모든 문명에 숨겨진 비밀, 수와 기하 ‘문명과 수학’ 제 1부 입니다. 이집트, 수의 기원 수는 어떻게 생겨났을까요?

곱셈과 나눗셈은 어떻게 시작했을까? 파이값도 모르면서 원의 면적을 어떻게 구했을까요?

수학의 모든 것은 이집트에서 출발한다. 3,500년 전 이집트 서기관이 썼던 파피루스 한 장에 의지해 인류 최초의 문명 이집트가

어떻게 왕국을 다스렸으며, 분배와 측량의 기술을 터득했는가를 살펴봅니다.

-지식반장

EBS 다큐프라임 / 문명과 수학 / 수의 시작.(이집트 수학)

이집트, 수의 기원 수는 어떻게 생겨났을까?

2년에 걸친 기획 조사와 자문 1년이 넘는 촬영 기간을 통해 이집트, 그리스, 인도를 거쳐

영국, 프랑스, 독일에 이르기까지 고대, 근현대 문명에 숨어있는 수학의 흔적을 고스란히

카메라에 담어아낸 작업, 6개국 100여명의 배우들이 직접 재연하는 방법으로

프로그램은 제작이 되었고 내용면으로는 수학적 깊이에 가장 공을 들였다

 수의 발견, 최초의 곱셈, 최초의 파이, 미적분등 난해한 수학내용을 최대한 쉽게

풀어내었다는 EBS 다큐프라임 5부작이 벌써 2회째 방송이 되었습니다.

제1부 수의 시작, 제2부 원론, 제3부 신의 숫자, 제4부 움직이는 세계 미적분

제5부 남겨진 문제들  모든 문명에 숨겨진 비밀 수와 기하

 EBS 다큐프라임 5부작, 그 시간속으로 들어가 세상의 모든 지식의 문으로

들어가는 수학의 열쇠를 풀어봅니다.

문명과 수학 첫번째 시간은 수의 시작입니다.

 

최초의 숫자가 시작된것은 바람이 풀풀 날리던 사막지대 이집트였습니다.

 

파라오의 전설과 함께 잠들어있었던것 눈에 보이지않는것, 4천년동안 홀로

기다려왔던 세상의 비밀스런 지식의 문이 지금 열리고 있습니다.

이집트는전혀다른 2개의 얼굴을 가진 땅이었습니다. 사막과 농토, 메마름과

풍요로움, 죽은자와 산자, 신화와 역사, 극단적인것들이 당연하게 공존하는 땅

도굴꾼이 들끓었던 곳,  옛 이름이 테베 였던곳, 람세르2세의

장례식장에서 나온 파피류스 1장에서 세상 모든 지식의 문이 시작됩니다.

 

서기관 아메스입니다.  견습 서기관들이 배워야할 문제를 정리하고 있는 중입니다.
왕국의 어려운 문제를 해결하는 2천년전부터 내려오는 문제들로 당시

수학은 고위관직자들만 알았던 학문으로 왕국의 미래를 생각해야하는 지식인들에겐

고된 시련이었다고 합니다. 그건 대체 무슨 문제였던것일까요?

당시 이집트의  권력은 단 한사람 파라오에게있었습니다. 신들이 완성시킨

 인물이라는  자신의 이미지에 공을들였던 탓에 생겨난것이 신전이었지요.

파라오는 안정과 생계를 빌고 , 사람들은 복종과 존경, 노동력을

바치는 암묵적 계약이  거의 2천년에 걸쳐 이루어졌습니다 

축구장 30개 크기,  134개의 기둥이 있는 최대규모의 신전 카르나크입니다.

 

거기에도 분명 수학적 이론이 숨겨져있을 것입니다.

하지만 그보다는 나일강에서 먼저 수학적 기원을 찾게됩니다. 사람들에게

수학을 만든신이 있었으니 바로 하피신(나일강의신) 이었기 때문이지요.

 1년 내내 거의 비가 오지 않는 이집트였지만 해마다 물난리가 났습니다

세계에서 가장 긴강으로  6천6백킬로미터에 이르는 나일강이었지요

이집트의 남쪽나라인 이티오피아 우간다의 우기에 내린비가  흘러 내려온것

이었지만 당시 사람들은 하피신이 가져다준다고  믿었다네고 합니다

상류에서 흘러내려온 퇴적물이  삼각주에 뿌려지며 비옥한 검은흙이 드러났습니다.

하지만 경계는 허물어 졌으니 파로오에겐 땅을 다시 찾아주어야하는 무거운 책임이

있었지요. 그 경계를 다시 짓는건 수학적 원의 넓이를 구해야하는

원의 넓이는 파이값 3,14를이용하면 됩니다. 하지만 당시엔 파이값이 없었지요.

서기관이 작성이 50번문제가 그 경계선을 새로 만드는 문제였습니다

가장작은단위 케트 폭 손가락4개 6개가모이면 구부린팔의 길이와똑같다

1큐빅 큐빅이100개모인게 1켓트 문제는 9켓트 팔이 900개가 모여야한다

 

서기관이 작성이 50번문제가 그 경계선을 새로 만드는 문제였습니다

한개의 손가락길이가 가장 작은 단위 손가락 4개가 모인길이를 6개 모으면

누구나 구부린 팔의 길이와 똑같다라고 합니다.

그것이 1큐빅으로 큐빅이 100개모인것이  1켓트였으며,

 문제는 9켓트로 말하고 있기에  팔이 900개가 모여야했습니다. 

 



그렇게 해서 지름이 9케롯의 넓이를 구하는 문제의 수식을 만들어갑니다.



지름이 9케롯의 원의 면적은 지름이 8케롯인 정사각형의 넓이와 같다라는 것을 알아냈다고 합니다.

원과 사각형의 넓이가 같다라는것을 조약돌을 이용하여 증명합니다

그건 파이값을 구해 넓이를 구하는 지금의 답과

거의 일치하고 있었습니다.

 

당시의 수학적 쓰임을 확인해보기위해 귀족 메나의 무덤을 찾아갑니다.

 수확량을 책정해 세금을 매기는 일을 했던 고위간부의 무덤으로

당시 국가재정은 농업생산이 거의 전부였기에 중요한 위치에 있었던 인물입니다.

정확하고 공평한 세금을 걷기위한 기록을하는것은 국가 재정의 중용부부능로

 해마다 강이 넘치고 난 후면 토지조사를 나갔다는데 세금을 걷기위한 전제가

 정확한 토지조사였기 때문이었답니다

 

이젠 본격적으로 범람후 나일강 유역의 농토를 나누었던 수학으로 들어가봅니다.

땅 넓이를 구하는 문제는 너무도 중요했기에  13문제가 냈었다고 하네요

무덤속 벽화엔 당시의 모습들이 생생하게 기록되어 있었습니다.

 

4* 5의 면적을 정했던 그 당시의 수학적 접근형태입니다. 4개의 조약돌을 하나로

배수로 넘어가게 되는데 그때마다 4개의 조약돌은 다시 하나로 정해집니다

1의 배수는 2, 2의 배수는 4 거기까지 넘어가면 5라는 숫자가 만들어집니다.

중간에 2배수를 제거하면 처음 시작했던 하나에 세번째의 4개가 더해져

5가 만들어지는 것이지요. 이것이 당시의 수학형태였다고 합니다.

 

또한 농격생활외 유목생활에서도 수 세기는 존재했습니다. 보이는것을 어떻게

 나누느냐에 따른 접근과 포식자들로부터 양을 지키기위한 이론에도 수학이

있었으니 거리감각이  수학의 중요한 이론이 되고 있었지요.

눈에 보이는 거리를 재는것부터 수학이 시작되었으며 그것을 어떤 방식으로

 나누느냐가 동물과 달리  인간들이 더 뛰어날수 있었던 요인이었습니다.

하늘과 땅, 먹을수 있는것과 먹을수 없는것, 거기에서 발전한것은

똑같은 숫자끼리 모아놓는 것이었습니다.

 

또한 당시 이집트인들은 소유한 양의 숫자만큼을  항아리에 돌로 담으면서

관리를 했다고 합니다. 겉의 구멍을 내서 안에 든 돌갯수를 표시했구요

하지만 돌과 구멍이 같은 의미라는것은 몰랐다고 하는군요

그러한 이론이 발달하여 여기까지오는데만  수만년이 흘렀구요.

이번엔 이집트 상형숫자속으로 들어가봅니다.



대기 하나는 1, 말발굽모양은 10

 

측량할때 쓰였던 밧줄은 100, 이집트 곳곳에 지천으로 널려있던 연꽃은 천

 
 

그렇게 해서 만들어진 숫자는 2012입니다.

백만이라고 하는 너무 큰숫자를 의미하는 상형문자는

놀라몬습의 사람입니다.

거대함을 향해 나아가는 피라미드에도 수의 비밀이 숨겨져있겠지요.

19세기이전까지는 그 누구도 이보다 좋은 건축물을 짓지못했다고 하는 곳입니다.

천정까지 12미터 4천5백년동안 버티고있지요. 조금씩 겹쳐서 쌓아올린 돌표면은

매끄럽고 실내공기는 무겁습니다.60미터를  내려와서애 마주한  풍경이지요

만명정도의 일꾼이 동원된 공사로  먹이고 입히는것 왕실의 운명을 좌우하는 공사였습니다

피라미드는 가장 어려운 수학문제로  지금도 풀리지않고 있답니다.

 

그 공사를 했던 사람들이 살았던 노동자의 마을입니다.



대공사자 부근에 항상 있는 마을로  노예가 아닌 월급을 받는 사람들이었답니다.

8일 일하고 이틀을 쉬웠으며 일이 있을때는 한달에 6일까지 휴가를 받았구요

그들이 급여로 받았던것은 빵, 거기에 분수가 있었습니다.

공평함이 깨지면 분쟁이 일어나지요 10명에게 9개의 빵을 어떻게 나누었을가요

 

그 분배에서 사용된것이 분수였습니다.

이집트인들이 썻던 분수는 분자가 모두 1인 숫자였으며 단 하나 예외가 2/3라고 합니다.

골고루 10으로 나눌수 있을만큼 분수를 만들어갑니다.

처음엔 2/3 남은 양으로 다시 나누니 1/5 다음을는 1/30

그렇게해서 9개의 빵을 10명에게 나누어주었습니다

지금의 계산식으로는 9/10 입니다.

수학의 발전은 그렇게 일상속에서 이루어졌습니다. 그것이 바로 수학의 보이지 않는 힘

84문제를 모두 정리한 필사한 아메스는 존재하는 모든사물과 비밀스런

모든 지식으로 들어가는 입구 그건 바로 수학이다라고 결론을 냈습니다

1부 수의 시작에서 마지막으로 만나는것은 한번 보기위해 1년을 기다려온것

도굴꾼들이 내다 판것이 돌고돌아 영국의 대영박물관에 안착한것  

모든 것이 시작된 처음으로 이끈 것 바로 아메스 수학 파피루스였습니다.



대영박물관에서 긴 파피루스를 보관할수 있는 단 하나의 장소

기원전 1650년경의 파피루스입니다.

그 파피루스엔 아메스가 필사한 문제도 있었습니다.

문명과 수학은 하나였습니다. 또한 수학은 우리의 삶의 학문이었습니다.

흔히 수학이 어려워질때마다 생활속에서 쓸데도 없는데 꼭 배워야 하는걸까

의문을 하곤 하는데 잘못된 생각이었던것이지요.

EBS 다큐프라임 문명과 수학 수의 시작이었습니다.

-----------------------------------

http://cafe.naver.com/goodstate/1710

스와미 바라티 크리슈나의 베다 수학 (Swami Bharati Krishna Tirtha's Vedic mathematics)은 인도의 수학자 스와미 바라타 크리슈나 티르타지가 발견하여 정리한 수학이다. 구전(口傳)으로만 전해온 브라만의 경전, 베다(Veda)경전의 계산과 수학에 관련된 수트라(Sutura)의 야타르바 베다(Atharva-veda)의 원문을 모두 해석하고 16개의 수트라 (간략한 형태로 표현된 법칙)과 13개의 술바수트라스(이 법칙의 파생)를 재구성한 베다수학은 인도 지역에서 전통적으로 발전해온 수학이다.

목차

 [숨기기] 

• 1 16가지 중요 수트라(격언)
• 2 베다 수학 덧셈
• 3 베다 수학 뺄셈
  • 3.1 1의 자리에 받아내림이 있는 경우
  • 3.2 백이나 천에서 1의자리가 0이 아닌 수를 뺄 경우
• 4 베다 수학 곱셈
  • 4.1 1의 자리가 작은 두 자리 수
  • 4.2 1의 자리가 큰 두 자리 수
  • 4.3 짝수와 1의 자리가 5가 있을 때
  • 4.4 25를 곱할 때
  • 4.5 4의 배수와 25의 배수를 곱할 때
  • 4.6 두 개의 수가 11~19 사이에 있을 때
  • 4.7 두 개의 수 중 10의 자리가 같을 때
  • 4.8 두 개의 수 중 1의 자리가 5일 때
  • 4.9 10의 자리가 같고 1의 자리끼리 더해서 10이 될 때
  • 4.10 1의 자리가 같고 10의 자리끼리 더해서 10이 될 때
  • 4.11 두 개의 수의 평균이 10의 배수가 될 때
  • 4.12 두 개 수가 100에 가까울 때
• 5 베다 수학 제곱
• 6 베다 수학으로 방정식 풀기
  • 6.1 베다 수학으로 연립방정식 풀기
• 7 베다 수학으로 1/19 계산하기
• 8 x를 곱하기
  • 8.1 5를 곱하기
  • 8.2 6을 곱하기
  • 8.3 7을 곱하기
  • 8.4 8을 곱하기
  • 8.5 9를 곱하기
• 9 관련 서적

[편집] 16가지 중요 수트라(격언)

1. 하나 앞의 수보다 하나 많게
2. 모두 9에서, 마지막은 10에서
3. 수직 방향으로, 십자 방향으로
4. 이항하여 적용하기
5. 사무카야가 같다면 사무카야는 0이다
6. 1이 비례하면 다른 것은 0이다
7. 더하기, 빼기
8. 완성 혹은 미완성
9. 미(적)분
10. 버리기
11. 특정적, 일반적
12. 마지막 수의 나머지
13. 끝자리 수, 뒤에서 두 번째 자리 수의 두 배
14. 하나 앞의 수보다 하나 적게
15. 덧셈의 결과
16. 모두 곱한 수(승수)

[편집] 베다 수학 덧셈

예를 들어 45+27은 다음과 같은 순서로 계산한다.

다음은 베다 수학의 덧셈 방법이다.

1. 40 + 20 = 60를 더하고 60을 기억한다.
2. 5 + 7 = 12을 더하고 2를 기억하고 10을 앞으로 넘긴다.
3. 60과 10을 더해 70을 기억한다.
4. 70과 2를 더한 72가 답이다.

비교를 위해 일반 수학의 덧셈 방법을 아래에 제시한다.

1. 5 + 7 = 12를 더하고 2을 기억하고 10을 앞으로 넘긴다.
2. 40 + 20 = 60을 더하고 60을 기억한다.
3. 60과 10을 더해 70을 기억한다.
4. 70과 2를 합친 72가 답이다.

[편집] 베다 수학 뺄셈

베다 수학의 뺄셈 방법은 다음과 같다.

[편집] 1의 자리에 받아내림이 있는 경우

예를 들어, 96-19는 다음과 같이 계산한다.

1. 뺄셈에서 빼는 수에 보수를 더하여 10의 배수로 만든다. (19 + 1 = 20)
2. 만들어진 10의 배수를 뺀다. (96 - 20 = 76)
3. (2)의 결과에 보수를 더한다. (76 + 1 = 77)

[편집] 백이나 천에서 1의자리가 0이 아닌 수를 뺄 경우

1000-146은 다음과 같이 계산한다.

1. 100의 자리와 10의 자리는 더해서 9가 되는 수의 보수를 찾는다. (1000 - 146 = 85[ ])
2. 1에 1의 자리를 더해서 10이 되는 수를 찾는다. (1000 - 146 = 854)

[편집] 베다 수학 곱셈

베다 수학의 곱셈 방법은 다양하다.

암산:예를 들어 45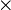27은 다음과 같은 순서로 계산한다. 다음은 인도 수학의 곱셈 방법이다.

1. 40와 20를 곱한 40 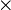20 = 800에서 800을 기억한다.
2. 40와 7를 곱한 40 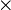7 = 280에서 80을 기억하고 200를 앞으로 넘긴다.
3. 800 대신, 800과 200를 더한 1000을 기억한다.
4. 5와 20을 곱한 5 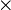20 = 100에서 0을 기억하고 100을 앞으로 넘긴다.
5. 1000 대신, 1000과 100을 더한 1100을 기억한다.
6. 5와 7을 곱한 5 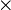7 = 35에서 5를 기억하고 30을 앞으로 넘긴다.
7. 80대신, 80 + 30 = 110에서 100과 10을 앞으로 넘긴다.
8. 1100 대신, 1100과 100을 더한 1200을 기억한다.
9. 기억한 숫자들인 1200 + 10 + 5 = 1215가 답이다.

필산1:교차 곱셈을 한다. 예를 들어, 53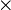77은 다음과 같은 순서로 계산한다.

1. 필산식을 쓴다.
2. 10의 자리 수 5와 7을 곱한 35를 기억한다.
3. 교차하여 5와 7, 3과 7을 각각 곱한 결과 35와 21을 더한 56을 기억한다.
4. 1의 자리 수 3과 7을 곱한 21을 기억한다.
5. 나란히 순서대로 쓴 뒤, 순서대로 쓴 후에 10이 넘는 수는 올림을 해서 계산한다.
6. (5)의 과정대로 하면, 35(5)6(2)1이 되므로, 4081이 답이 된다.

필산2:보수 계산을 한다. 예를 들어, 88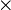97은 다음과 같은 순서로 계산한다.

1. 필산식을 쓴다.
2. 100을 기본수로 하여 88과 97의 보수 12와 3을 각각의 수 오른쪽에 적는다.
3. 서로 교차하여 뺀 수(88 - 3, 97 - 12) 85를 기억한다.
4. 보수 12와 3을 곱한 수 36을 기억한다.
5. (2)의 수와 (3)의 수를 나란히 쓰면 답이 된다. 순서대로 쓴 후에 10이 넘는 수는 올림을 해서 계산한다.
6. (5)의 과정대로 하면 8536이 답이 된다.

일반 수학의 곱셈과 차이점은 덧셈에서도 보았듯이 높은 자리수 부터 먼저 계산해서 아래로 내려간다.

[편집] 1의 자리가 작은 두 자리 수

36×11은 다음과 같이 계산한다.

1. 10의 배수 + 1의 자리로 곱하는 수를 변형한다. (11 = 10 + 1)
2. 10의 배수를 곱한다. (36 × 10 = 360)
3. 곱하려는 수 ×1의 자리수를 (2)에 더한다. (360 + (36 × 1) = 396)

[편집] 1의 자리가 큰 두 자리 수

32×19는 다음과 같이 계산한다.

1. '10의 배수 - 보수'로 곱하는 수를 변형한다. (19 = 20 - 1)
2. 10의 배수를 곱한다. (32 × 20 = 640)
3. 곱하려는 수 × 보수를 (2)에 뺀다. (640 - 32 × 1 = 608)

[편집] 짝수와 1의 자리가 5가 있을 때

14×45는 다음과 같이 계산한다.

1. 곱하려는 수를 'x × 2'로 변형한다. (14 = 7 × 2)
2. '2'와 곱하는 수를 곱한다. (2 × 45 = 90)
3. 'x'와 (2)를 곱한다. (7 × 90 = 630)

[편집] 25를 곱할 때

48×25는 다음과 같이 계산한다.

1. 곱하는 수를 나눗셈으로 변형한다. (25 = 100 ÷ 4)
2. 곱하려는 수에 '100'을 곱한다. (48 × 100 = 4800)
3. (2)를 4로 나눈다. (4800 ÷ 4 = 1200)

[편집] 4의 배수와 25의 배수를 곱할 때

24×75는 다음과 같이 계산한다.

1. 곱하려는 수를 'x × 4'로 변형한다. (24 = 6 × 4)
2. 곱하는 수를 'y × 25'로 변형한다. (75 = 3 × 25)
3. 'x × y'에 '100'을 곱한다. (6 × 3 × 100 = 1800)

[편집] 두 개의 수가 11~19 사이에 있을 때

13×12는 다음과 같이 계산한다.

1. 곱하려는 수에 곱하는 수의 1의 자리를 더한다. (13 + 2 = 15)
2. 1의 자리끼리 곱한다. (3 × 2 = 6)
3. (1)에 10을 곱해서 (2)를 더한다. (15 × 10 + 6 = 156)

[편집] 두 개의 수 중 10의 자리가 같을 때

23×22는 다음과 같이 계산한다.

1. 곱하려는 수에 곱하는 수의 1의 자리를 더한다. (23 + 2 = 25)
2. 1의 자리끼리 곱한다. (3 × 2 = 6)
3. (1)에 '10의 자릿수 × 10'을 곱해 (2)를 더한다. (25 × 2 × 10 + 6 = 506)

[편집] 두 개의 수 중 1의 자리가 5일 때

55×75는 다음과 같이 계산한다.

1. 10의 자리끼리 곱한다. (5 × 7 = 35)
2. 10의 자리끼리 더해서 2로 나눈다. ((5 + 7) ÷ 2 = 6)
3. (1)과 (2)를 더해서 100을 곱해 25를 더한다. ((35 + 6) × 100 + 25 = 4125)

[편집] 10의 자리가 같고 1의 자리끼리 더해서 10이 될 때

81×89는 다음과 같이 계산한다.

1. 10의 자릿수 + 1과 10의 자리를 곱한다. ((8 + 1) × 8 = 72)
2. 1의 자리끼리 곱한다. (1 × 9 = 9)
3. (1)에 100을 곱해 (2)를 더한다. (72 × 100 + 9 = 7209)

[편집] 1의 자리가 같고 10의 자리끼리 더해서 10이 될 때

43×63은 다음과 같이 계산한다.

1. 10의 자리끼리 곱해서 1의 자리를 더한다. (4 × 6 + 3 = 27)
2. 1의 자리끼리 곱한다. (3 × 3 = 9)
3. (1)에 100을 곱하고 (2)를 더한다. (27 × 100 + 9 = 2709)

[편집] 두 개의 수의 평균이 10의 배수가 될 때

19×21은 다음과 같이 계산한다.

1. 두 개의 수의 평균을 구한다. ((19 + 21) ÷ 2 = 20)
2. 평균에 대한 최솟값의 보수를 구한다. (20 - 19 = 1)
3. 평균 × 평균에서 보수 × 보수를 뺀다. (20 × 20 - 1 × 1 = 399)

[편집] 두 개 수가 100에 가까울 때

98×97은 다음과 같이 계산한다.

1. 100에 대한 두 개 수의 보수를 구한다. (100 - 98 = 2, 100 - 97 = 3)
2. 100에서 두 개의 보수를 더한 수를 뺀다. (100 - (2 + 3) = 95)
3. (2)에 100을 곱해서 2 개의 보수를 곱한 수를 더한다. (95 × 100 + 2 × 3 = 9506)

[편집] 베다 수학 제곱

제곱의 계산 방법은 다음과 같다.

1. 가장 가까운 제곱 수인 10⁹ ~ 10¹⁰을 쓴다. 이때, 지수가 10을 넘지 않도록 한다.
2. 최대 수 9에서 최소 수 1을 뺀다. (9 - 1 = 8) 그리고 왼쪽에 답을 쓴다.
3. 그리고 오른쪽의 제곱을 계산하여, 1²을 계산한다. 그리고 오른쪽에 그 답을 쓰면 9의 제곱은 81이 된다.

Similarly, 8² = 64, 7² = 49.

다음은 거듭제곱 계산 예제이다:

이때 위 5개 식에서의 공통 공식은 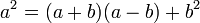이다. 이 공식에서 역시 지수가 10을 넘지 않도록 한다.

[편집] 베다 수학으로 방정식 풀기

이 부분은 사무카야가 같다면 사무카야는 0이다 부분에 나온다.

수학에서 주어진 방정식을 푸는 것은 어려운 일이다. 산스크리트어로는 사무카야라고 부른다. 여기서 언급하는 방정식 역시 베다 수학으로 풀 수 있다. 그 중에서 가장 간단한 일차방정식인 "12x + 3x = 4x + 5x"를 풀어보자. 여기서 일차방정식의 해 "x"는 x = 0이다. 여기서 사무카야가 같다면 사무카야는 0이다가 베다 수학의 또 한가지 수트라로 나온 것이다. 그리고 또 다른 일차방정식인 (x + 7) (x + 9) = (x + 3) (x + 21)을 풀어보자. 이 방정식(사무카야) 역시 수트라의 원리를 이용하면 7 × 9 = 3 × 21로 나와서 x = 0 이 답이 된다. 그렇다면 분수방정식은 어떻게 푸는 건지 분수방정식 1/ (2x − 1) + 1/ (3x − 1) = 0을 풀어보자. 이것을 일차방정식으로 간략화하면 5x – 2 = 0이 나온다. 이 일차방정식의 답은 x = 2/5이다.

그러면 계수가 높고 분수의 분자와 분모가 모두 일차식으로 되어 있는 분수방정식은 어떻게 푸는 건지 아래의 주어진 방정식으로 풀어 보자.

위 분수방정식을 일차방정식화하면 4x + 16 = 0이 되어서 답은 x = −4가 된다.

이제 이 답이 어떻게 나오는지 알아보자. 베다 수학을 이용하여 위의 분수방정식을 풀 때 필요한 두 가지는 N₁, N₂, D₁, D₂이다. N₁/D₁ = N₂/D₂이고 N₁ + N₂ = D₁ + D₂ 라면 합은 0이 된다. 위 식에서의 해를 구하기 전에 나오는 답은 x² 이다. 그리고, 만약 N₁ − D₁ = N₂ − D₂라면 사무카야는 0이 된다. 그리고 그 방정식의 해는 제곱근으로 나오며 무리방정식의 형태로 된다.

아래의 주어진 분수방정식과 위에서 언급한 식으로 풀어 보자.

그러면 D₁ + D₂ = D₃ + D₄ = 2x − 16일 때는 어떻게 되는지 알아보면 답은 x = 8이다.

위의 주어진 분수방정식을 간단하게 해 보자. 약분을 하고 분수를 없애면 다음과 같이 정수형의 삼차방정식으로 된다.

여기서 일차방정식으로 줄이면 x − 3 + x − 9 = 2 (x − 6), (x − 6) = 0 or x = 6이 된다. 그러나 진짜는 위의 방정식을 복소수화시키는 것이므로 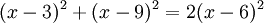를 복소수화 시키면

이 되어서 일차방정식은 N₁ + D₁ = N₂ + D₂ = 2x + 8이 되어 x = −4가 된다.

[편집] 베다 수학으로 연립방정식 풀기

아래의 수식은 모두 x와 y의 계수가 보통과 다르게 큰 숫자로 되어 있다. 그러나 잘 보면 아래의 두 개의 식은 비례 관계가 있음을 알 수 있다. 예를 들면 다음과 같다:

6x + 7y = 8

19x + 14y = 16

위의 두 방정식에서 잘 보면 y의 계수가 위쪽은 7, 아래쪽은 14이므로 1 : 2의 비를 이루고 있음을 알 수 있다. 따라서 나머지 1 : 2, 즉 8과 16은 0이 되어 x = 0이 된다. 이렇게 하면 위 연립방정식은 x = 0, y = 8/7의 해를 갖는다.

(다른 예:

19x + 14y = 16의 절반은

(19/2)x +7y = 8.

이렇게 x의 계수가 정확한 비가 되지 않을 경우, 비가 없는 경우이므로, 반드시 2로 나누어야 한다!)

이렇게 하여 연립방정식을 만들면

6x + 7y = 8

12x + 14y = 16

연립방정식 만들기는 아주 쉽다. 아래의 형식을 그대로 따라서 x, y, 그리고 z의 계수를 정하여 만들면 된다:

ax + by + cz = a

bx + cy + az = b

cx + ay + bz = c

위에서는 x = 1, y = 0, z = 0.

아래의 방정식은 x와 y의 계수가 서로 바뀌어 있다. 즉 위쪽은 x의 계수가 45, y의 계수가 23이지만, 아래쪽은 x의 계수가 23, y의 계수가 45인 형태이다:

45x − 23y = 113

23x − 45y = 91

더하면 : 68x − 68 y = 204 → 68 (x − y) = 204 → x − y = 3.

빼면 : 22x + 22y = 22 → 22 (x + y) = 22 → x + y = 1.

다시 더하면 : 2x = 4이므로 따라서 x = 2가 된다.

또다시 빼면 : – 2y = 2이므로 따라서 y = –1이 된다.

따라서 위 방정식의 해집합은 {2, -1}이 된다.

[편집] 베다 수학으로 1/19 계산하기

분수 1/19는 2와 5 모두 나누어 떨어지지 않는다. 그러면 직접 1/19를 필산하여 계산하는 수밖에 없다. 그러나 이것은 매우 복잡하고 많은 시간이 걸린다. 2와 5 또는 10 만 있으면 1/19를 구할 수 있다.

일단 맨 처음 1을 쓴다.

1

그리고 1을 두 배한 수 2를 1 앞에 쓴다.

21

2를 두 배 곱한 수 4, 4를 두 배 곱한 수 8를 각각 4는 2 앞에, 8은 4 앞에 쓴다.

421 → 8421

그렇게 되면 다음과 같이 자리올림수 1이 나온다.

684211 ← 올림수

그리고 다시 곱하는데 이때 곱하는 수는 6과 2를 곱하여 12 가 된다. 여기서 자리올림수 1 을 더하여 13을 쓴다.

3684211 ← 올림수

계속하게 되면 다음과 같이 된다.

7368421 → 47368421 → 947368421                 1

지금까지 우리는 9자리 수까지 계산하였다. 계산하여 18 자리가 되어야 한다. 지금까지 계산한 값의 1/2의 자릿수를 최소가 되게 배열하면 다음과 같이 된다.

052631578947368421

계산한 결과는 1/19 = 0.052631578947368421 이 된다.

다음은 계산 과정을 나타낸 것이다.

121421842168421 (올림수 1) – 8을 두 배하면 16이 되는데, 이 때는 일의 자리수만 쓴다. 올림수는 그대로 남겨둔다.368421 (올림수 1) – 6을 두 배하면 6*2 + 올림수 1 = 13이 되는데, 역시 일의 자리수만 쓴다. 올림수는 그대로 남겨둔다.18자리까지 계산하게 되면 (19–1. 이것은 1/29의 경우는 28 자리까지) 다음과 같이 된다.1/19 = 052631578947368421       10100111101011000

[편집] x를 곱하기

[편집] 5를 곱하기

1. 의외로 간단한 문제이다. x의 일의 자리 수가 1씩 올라갈 때마다 곱셉한 수도 5씩 올라가게 된다.
2. 이렇게 하면 곱한 수는 항상 홀수가 된다.

42x5=210 ← 홀수

4=2,2=1

43x5=215 ← 홀수

[편집] 6을 곱하기

1. 5와 곱하는 방법과 역시 간단한 방법이다.
2. x의 일의 자리 수가 1씩 상승하면, 곱셈수에 5를 더한다.

6 × 357 = 2142
계산하면,
7 은 홀수이므로 5를 더한다. 12가 되는데, 10을 초과하므로 2를 쓰고 1은 올림수로 남겨둔다.
5 + 1/2 of 7 (3) + 5 (5를 더한다) + 1 (자리올림) = 14. 4를 쓰고, 1은 올림수로 남겨둔다.
3 + 1/2 of 5 (2) + 5 (5를 더한다) + 1 (자리올림) = 11. 1을 쓰고, 1은 올림수로 남겨둔다.
0 + 1/2 of 3 (1) + 1 (자리올림 한다) = 2. 2를 쓴다.

[편집] 7을 곱하기

1. 수의 1/2를 더한다.
2. 수가 홀수이면 5를 더한다.

ex) 46×7=322

[편집] 8을 곱하기

1. 10에서 1의 자리수를 뺀다.
2. 9에서 10의 자리수를 뺀다.
3. 두 개의 뺄셈 결과를 더한다.
4. 그리고 2 를 더한다.

[편집] 9를 곱하기

이 방법은 어려우므로 차근차근 해 보자.

1. 10에서 1의 자리수를 뺀다.
2. 만약 계속 계산이 가능하면 9에서 10의 자리수를 빼고 더한다.
3. 마지막으로 1을 뺀 값을 쓴다.

2,130 × 9 = 19,170

1. 10 - 0 = 10. 0을 쓰고, 1은 자리올림수로 남겨둔다.
2. 9 - 3 = 6; 6 + 0 + 1 (자리올림) = 7. 7을 쓴다.
3. 9 - 1 = 8; 8 + 3 = 11. 1을 쓴다. 1은 자리올림수로 남겨둔다.
4. 9 - 2 = 7; 7 + 1 + 1 (자리올림) = 9. 9를 쓴다.
5. 2 - 1 = 1. 1을 쓴다.

[편집] 관련 서적

• 《인도 베다수학 매일매일 두뇌트레이닝 : 세상을 지배하는 숫자의 비밀 인도수학 시크릿》, 손호성, 아르고나인, 2008, ISBN 978-89-961034-1-7

원본 주소 "http://ko.wikipedia.org/w/index.php?title=스와미_바라티_크리슈나의_베다_수학&oldid=9781836"