민코프스키 (Hermann Minkowski) (1864년 6월 22일 - 1909년 1월 12일) 러시아 태생의 독일 수학자.
수론의 문제를 기하학적인 방법을 사용하여 푸는 기하학적 수론, 수리물리학, 상대론등에 업적을 남겼다.
헤어만 민코프스키는 러시아에서 태어났으나 어렸을 때 당시 동프러시아인 쾨니히스베르크(Königsberg)로 가족과 함께 이주해 독일의 베를린 대학, 쾨니히스베르크 대학등에서 교육받았다. 박사학위는 1885년 쾨니히스베르크에서 받는다. 이후 본, 쾨니히스베르크, 취리히 등에서 강의하며, 취리히 시절에는 아인슈타인을 가르치기도 한다.
민코프스키는 n 개의 변수를 갖는 2차식(quadratic forms)을 연구하는 과정에 n 차원 공간의 기하학적 성질과 관련된 것을 알아차린다. 1896년 출판한 저서 수의 기하학에서 수론의 문제들을 기하학적인 방법과 연관시킨다.
1902년 당시 수학의 중심지였던 괴팅겐에 오랜 친구였던 다비드 힐베르트의 도움으로 수학교수 자리를 얻어 연구한다.
1907년에 특수 상대성 이론이 민코프스키 공간이라 불리는 비유클리드 공간을 이용해 쉽기 이해될 수 있다는 사실을 알아차린다. 민코프스키 공간에서 시간과 공간은 서로 상관없는 두 개체가 아니라, 합쳐져 4차원 시공간을 이룬며, 그를 통해 특수 상대론의 로렌츠 기하가 잘 표현된다. 이 기하학적인 방법은 나아가 아인슈타인의 일반 상대성 이론을 이해하는 데에도 도움이 되었다. 1908년 9월 21일 그가 제80회 독일 자연과학자 모임에서 행한 연설의 모두는 지금도 유명하다.
- The views of space and time which I wish to lay before you have aprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.
- 지금 제가 여러분 앞에 제시하려는 시간과 공간에 대한 생각은 실험 물리학에서 나온 것이며, 그래서 더욱 힘이 있습니다.
- 이 생각은 과격합니다.
- 앞으로 공간따로, 시간따로라는 개념은 그림자속으로 사라질 것이고, 단지 그 둘이 합쳐진 그것만이 독립적인 실체로 남아있을 것입니다.
-------------------------------------------------------------------------
민코프스키 시공간을 이해하기 위해서는
우선 유크리드공간과 비교하배노느것이 도움이될 것이다.
3차원 유클리드 공간은 위상적(topolgical) 구조, 아핀(affine) 구조, 그리고 계량적(metric) 구조를 지니고 있는 기하학적 구성이다.
위상적 구조에 의하여 기하학적 대상들의 연속성과 불연속성에 관한 사실들이 결정될 수 있으며, 그것에 의하여 공간 상에서 대상의 연속성을 보존하는 위상적 변환이 가능해진다. 아핀 구조는 두 점들 사이에 유일한 직선이 존재한다는 사실을 결정하며, 이에 따라 아핀 변환은 아핀 구조를 지니고 있는 공간 상에서 선 혹은 면의 직선성을 보존하는 함수가 된다.
점들 사이의 거리 혹은 선의 길이에 관한 사실은 계량적 구조에 의하여 결정되며, 그러한 사실들을 보존하는 변환은 균등(isometry) 변환이라고 불린다. 어떠한 기하학적 대상이 균등 변환된다면, 원래의 대상과 변환된 대상은 합동(congruence) 관계를 지닐 것이다.
이러한 구조들을 지니고 있는 3차원 유클리드 공간은 일반적으로 데카르트 좌표계에 의하여 표상된다.
데카르트 좌표계는 3차원 유클리드 공간에서 기본적인 존재자로 도입된 점들에 개별적인 실수들을 할당하는 함수들의 집합으로 생각될 수 있다.
이러한 좌표 함수는 3차원 유클리드 공간 내의 한 점이 논항으로 주어졌을 때 각각 한 가지의 실수를 값으로 산출하는 축 함수들 세 가지로 구성되어 있을 것이다. 가령, 어떠한 점 p가 주어졌을 때, 그것에 할당되는 좌표값은 x축 좌표 함수의 값인 3, y축 좌표 함수의 값인 6, z축 좌표 함수의 값인 9로 구성된 삼중체인 (3,6,9)가 될 수 있다.
따라서, 이러한 데카르트 좌표계의 도입은 3차원 유클리드 공간의 속성에 대한 대수적인 연산을 가능케 한다. 그렇다면 3차원 유클리드 공간에 대한 이러한 대수적인 표상은 어떠한 방식으로 그것이 지니고 있는 기하학적 구조들을 표상할 수 있을 것인가?
먼저, 기하학적 대상의 연속성에 관한 사실들을 결정하는 위상적인 구조는 좌표 함수의 연속성에 의하여 표상될 수 있을 것이다. 즉, 모든 좌표 함수가 연속 함수라는 가정에 의하여 공간의 위상적 구조가 대수적으로 표상될 수 있는 것이다. 다음으로, 유클리드 공간의 아핀 구조는 데카르트 좌표계에서의 선형 방정식에 의하여 표상될 것이다. 즉, '이차원적' 유클리드 공간에서의 특정한 직선은 그것에 포함된 점들이 데카르트 좌표계에 할당된 방식에 따라 y=ax+b와 같은 형식의 선형 방정식으로 표상될 수 있는 것이다. 마지막으로, 유클리드 공간의 거리적 구조는 '거리 함수'의 도입을 통하여 데카르트 좌표계에 반영될 수 있다. 즉, 유클리드 공간에서 두 점 사이의 거리는 두 점에 대응되는 데카르트 좌표계의 좌표들을 논항으로 삼는 거리 함수의 값을 통하여 표상될 수 있는 것이다. 피타고라스 정리를 통하여 그러한 거리 함수가 다음과 같다는 것은 쉽게 알려진다.
![]()
즉, 어떠한 두 점 p,q 사이의 거리는 p,q의 거리 함수의 값, 즉, p에 대응되는 x-좌표값과 q에 대응되는 y-좌표값의 차이를 제곱한 값, 각각의 y-좌표값의 차이를 제곱한 값, 그리고 각각의 z-좌표값의 차이를 제곱한 값의 합의 제곱근에 대응되는 것이다. 우리는 p,q 사이의 거리와 p,q의 거리 함수의 값이 지니는 관계에 주목할 필요가 있다. 특정한 거리 함수 값인 D(u,v)는, 그것에 특정한 계량 단위가 할당되지 않는 이상, 어떠한 기하학적 의미도 지니고 있지 않다. 하지만 이와 달리, 어떠한 거리 함수 값들 사이의 '비율'은 그 자체만으로 기하학적인 의미를 지니고 있다. 가령, 우리는 세 좌표 사이의 두 거리 함수의 비율이 1:2라는 사실만을 통하여 유클리드 공간에서 세 좌표에 대응하는 세 점 사이의 거리의 비율이 1:2라고 올바르게 추론해낼 수 있는 것이다. 이것은 특정한 대수적 사실은 우리가 도입하는 측정 단위나 계량법과 관계없이 특정한 기하학적 사실에 대응된다는 것을 의미하며, '게이지 자유(gauge freedom)'라는 용어가 지칭하는 바이다.
뉴턴 역학은 이러한 기하학적 구조를 지니고 있는 3차원 유클리드 공간, 그리고 그러한 유클리드 공간의 존속이 이루어지는 1차원적 절대 시간에 관한 역학이다. 하지만, 뉴턴 역학은 상대성 이론에 대체되며, 상대성 이론은 시간과 공간의 구조가 구분되지 않는 4차원적 시공간의 도입을 요구한다. 이러한 상대론적 요구에 부합하는 것이 바로 민코프스키(Minkowski) 시공간이다.
먼저, 민코프스키 시공간은 기본적으로 사건들의 집합과 그 사건들을 잇는 세계선을 도입한다. 민코프스키 시공간에서의 사건과 세계선은 각각 3차원 유클리드 공간에서의 점과 선에 유비될 수 있다. 다음으로, 민코프스키 시공간의 위상학적 구조와 아핀 구조는 3차원 유클리드 공간의 그것과 ㅡ민코프스키 시공간은 3차원 유클리드 공간과 달리 시간과 공간이 동일한 방식으로 그러한 구조를 예화한다는 것을 제외하면ㅡ 다를 바가 없다. 하지만, 민코프스키 시공간은 3차원 유클리드 공간에 도입된 거리적 구조와 전혀 다른 구조를 지니고 있다. 더 구체적으로 말하자면, 민코프스키 시공간에서의 두 '사건' 사이의 구분은 3차원 유클리드 공간에서의 두 점 사이의 구분과는 전혀 다른 방식으로 실현된다는 것이다.
<유클리드 공간에서, 두 점들 사이의 구분은 두 점들 사이의 거리에 의하여 측정된다. 그러한 거리는 순수하게 공간적이고, 그리고 항상 양수이다. (민코프스키) 시공간에서, 두 사건들 사이의 구분은 두 사건들 사이의 불변적인 간격에 의하여 측정된다. 그것은 두 사건들 사이의 공간적인 구분 뿐만 아니라 시간적 구분 까지도 설명한다. 두 사건들 사이의 간격 s^2은 다음과 같이 정의된다:
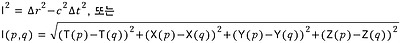
여기서 c는 빛의 속력이고, △r과 △t는 각각 두 사건들 사이의 공간 좌표 차이와 시간 좌표 차이를 나타낸다. 시공간의 geodesic이라 불리는 세계선들의 특정한 유형들은, 거리가 시공간 간격으로 정의되었을 때, 어떠한 두 사건 사이의 가장 가까운 경로이다. 'geodesic' 개념이 일반 상대성 이론에서 중요한 이유는 geodesic 운동이 시공간에서 "순수한 운동", 즉, 어떠한 외부적 영향도 주어지지 않은 관성 운동으로 생각될 수 있기 때문이다. 시공간 간격은 시간적 구분(c^2△t^2)과 공간적 구분(△r^2) 중 어떠한 것이 큰 가에 따라 세 가지 구분되는 유형으로 분류될 수 있다.>
두 사건 사이의 공간적 구분과 시간적 구분이 동일한 경우, 즉, 간격이 0인 경우에 두 사건은 빛을 닮은(lightlike) 관계이고, 공간적 구분과 시간적 구분의 차이가 음수이거나 양수인 경우엔 각각 시간을 닮은(timelike) 관계, 공간을 닮은(spacelike) 관계일 것이다. 이러한 '간격'이라는 양이 민코프스키 시공간에서 사건들 사이의 원초적인 관계로서 도입된 동기는 게로치의 논의에서 어느 정도 분명하게 발견된다(http://blog.naver.com/atp174/20204465483).
3차원 유클리드 공간은 데카르트 좌표계에 의하여 표상될 수 있다. 또한, 특정한 데카르트 좌표계를 통한 운동의 기술은 갈릴레이 변환에 의하여 구분되는 데카르트 좌표계를 통하여 기술될 수 있다. 이와 달리, 민코프스키 시공간은 로렌츠 좌표계에 의하여 표상될 수 있으며, 로렌츠 변환에 의하여 구분되는 로렌츠 좌표계들 사이의 관계가 명시될 수 있다. 로렌츠 좌표계는 데카르트 좌표계가 3차원 유클리드 공간의 위상학적 구조와 아핀 구조를 표상하는 것과 동일한 방식으로 민코프스키 시공간의 위상학적 구조와 아핀 구조를 표상한다. 하지만, 로렌츠 좌표계에서 사건들은 그것들 간의 거리가 아닌 간격에 의하여 구분된다. 거리의 경우와는 달리, 두 사건은 간격이 0인 경우에도 구분될 수 있으며, 양수 뿐만 아니라 음수의 간격 또한 지닐 수 있다.
민코프스키 시공간에서의 간격은 3차원 유클리드 공간에서의 거리와 마찬가지로 불변량으로서 다뤄진다. 3차원 유클리드 공간에서, 관찰자의 공간적 경로에 따라서 두 점 사이의 거리가 다르게 측정될 수 있지만 거리 함수의 값에 의하여 표상되는 직선 거리는 관찰자의 상태와 독립적으로 결정될 수 있다. 이와 유사하게, 민코프스키 시공간에서는, 관찰자의 시공간적 경로 혹은 세계선의 궤적에 따라서 두 사건 사이의 간격이 다르게 측정될 수 있지만, 간격은 관찰자의 상태와 독립적인 방식으로 결정될 수 있는 절대적인 측정치를 지니고 있는 것이다. 이와는 다르게, 민코프스키 시공간에서는, 거리나 시간과 같은 양은 관찰자의 상태와 독립적으로 결정될 수 있는 불변량으로서의 지위를 박탈당하게 되는 것이다. 그것이 바로 '시간과 공간의 상대성'이란 용어가 가리키고자 하는 바이다.
--------------------------------------------------------------
민코프스키는 4차원 시공간에서 물체의 위치를 나타내는 세계선(world-line)이란 개념을 만들었단다.
또 세계선으로 특수상대성이론에 나오는 동시성 문제, 시간의 지연, 길이의 축소 등이 일어나는 이유를 간단하게 그림으로 설명하였단다. 공간력이 뛰어난 우뇌형 인간이라면 이 글을 읽는 편이 특수상대성이론을 이해하기가 휠씬 쉽겠지. 지금부터 세계선으로 특수상대성이론을 이해해 보자.
■ 세계선
세계선이란 4차원 민코프스키 공간에 표시된 운동의 궤도를 말한단다. 일단 그림으로 세계선이 무엇인지 살펴보자.
[그림] 1차원 철로 위에 기차가 있고, 그 기차의 중앙점을 M이라고 하자.
그림과 같이 철로 위에 기차가 있다. 그리고 그 기차의 중앙점을 M이라고 하자. 이 기차의 위치를 4차원 시공간좌표 위에 그려 보자. 아래의 그림에서, x축은 거리이고, y축은 시간으로, 4차원 시공간을 표시하는 그래프이다. 공간은 3차원이지만, 지면에 표기해야 하는 관계 상, 1차원 x만 표기하도록 하자.
[그림]철로 위에 서 있는 기차의 세계선
시간 t = 0 일 때 기차의 위치 M은 x축 위에 있다. 이후 시간이 흘러 t = 1, t = 2, t = 3... 으로 변하더라도 정지한 기차의 x값은 변하지 않는다. 그림 위의 굵은 화살표 선은 시간의 흐름에 따른 기차의 위치 M을 나타낸단다. 이때 이 굵은 화살표 선을 세계선이라고 부른단다. 즉, 세계선은 4차원 시공간에서 기차의 운동 궤도를 나타낸 선이 된단다.
만약, 기차가 오른쪽이나 왼쪽로 움직이면, 세계선은 어떻게 될까?
기차가 정지한 경우에는 시간(t)에 따라 거리(x)가 변하지 않았지만, 기차가 움직이면 시간(t)에 따라 거리(x)가 변하겠지.
[그림] 기차가 오른쪽이나 왼쪽로 움직일 때의 세계선
위의 그림은 보면 기차가 오른쪽이나 왼쪽로 움직일 때의 세계선을 나타낸단다. 오른쪽으로 기울어진 세계선은 기차가 오른 쪽으로 움직일 때이고, 왼쪽으로 기울어진 세계선은 기차가 왼쪽으로 움직일 때의 세계선이란다. 만약 기차의 속도가 느리면, A와 같이 되고, 속도가 빠르면 B와 같이 되겠지.
이제 빛의 세계선을 그려보자.
[그림] 빛의 세계선.
빛의 세계선도 기차의 세계선과 다름이 없단다. 다만 속도가 더 빠른 것 뿐이란다. 위의 그림에서 내가 원점 O에 서있다. 내 곁에 있던 빛이 내게서 멀어지면 빛의 세계선은 위의 왼쪽 그림처럼 되겠지. 또, 내게서 멀리 떨어져 있는 빛이 다가오면 오른쪽 그림처럼 되겠지.
민코프스키는 4차원 공간에서, 시간(t)를 거리로 환산하려면 광속 c(30만km/s)를 곱해 주어야 한다고 했지. 따라서 y축 시간 t에 광속 c(30만km/s)를 곱한 눈금으로 사용하면, 세계선의 기울기는 45도가 되겠지. 이때, 어떤 물체의 세계선도 기울기가 45도 보다 작을 수는 없단다. 빛보다 빠를 수는 없으니까. 그리고 앞으로 나오는 모든 그림에서는 y축을 시간 t에 광속 c(30만km/s)를 곱한 눈금으로 사용할거야. 따라서 빛의 세계선은 항상 45도로 기울어진다는 점을 명심해라.
■ 동시성의 파괴
이제 세계선으로, 앞에서 이야기한 '동시성의 파괴'에 대한 이야기를 해보자.
[그림] 정지한 기차와 움직이는 기차의 세계선
위의 왼쪽 그림은 정지한 기차의 세계선이고, 오른쪽 그림은 움직이는 기차의 세계선이다. 그림에 있는 M은 기차의 중앙점이고, A는 기차의 왼쪽 끝점이고, B는 오른쪽 끝점이며. 3개의 선은 기차의 중앙점과 왼쪽 끝점, 오른쪽 끝점의 세계선이란다.
그런데 이 그림에서 꼭 알아야 할 것이 하나 있단다. 위의 왼쪽 그림과 오른쪽 그림에 있는 기차를 보면, 기차의 길이가 똑 같게 보이지. 하지만 특수상대성이론에 따르면, 정지한 기차(왼쪽 그림의 기차)의 길이보다 움직이는 기차(오른쪽 그림의 기차)의 길이가 짧아진단다. 하지만, 그렇더라도 여기에서는 실제 길이를 무시하자. 짧아지는 길이에 대해서는 아래에서 자세하게 설명할 예정이야.
이제 기차의 양쪽 끝에서 동시에 번개가 쳤다고 가정해보자.
[그림] 기차의 양쪽 끝에서 번개가 치고, 번개에서 나온 빛이 기차의 중앙으로 퍼져나가는 모습
이제, 기차의 양쪽 끝에서 기차의 중앙으로 이동하는 빛의 세계선을 그려보자. 위에서 이야기한 대로 빛의 세계선은 45도 경사지게 그리면 되겠지.
[그림] 기차의 양쪽 끝에서 기차의 중앙으로 이동하는 빛의 세계선(점선)
위의 그림에서, 점선 AM'는 기차의 왼쪽 끝(A)에서 출발하여 중앙(M')에 도달하는 빛의 세계선이란다. 또, 점선 BM'는 기차의 오른쪽 끝(B)에서 출발하여 중앙(M')에 도달하는 빛의 세계선이란다.(빛의 세계선인 점선들은 모두 x축과 45도를 이루고 있단다.)
정지해 있는 기차(왼쪽 그림)를 보면, 양쪽에서 오는 빛이 같은 시간에 도착한다. 하지만, 움직이는 기차(오른쪽 그림)를 보면, 양쪽에서 오는 빛에 같은 시간에 도착하지 않는 것을 알 수 있지. 즉, 정지한 기차의 중앙에 서 있는 사람(혹은 철로 변에 서 있는 사람)은 동시에 번개를 쳤다고 이야기하겠지만, 움직이는 기차의 중앙에 서 있는 사람을 보면 오른쪽에서 먼저 번개를 쳤다고 이야기하겠지.
■ 동시눈금선
이제 이야기를 한발짝만 더 나아가 보자.
[그림] 기차의 중앙에서 플래시가 터진 후, 플래시의 빛이 기차의 왼쪽 끝과 오른쪽 끝에 있는 거울에 반사되어 돌아오는 모습
위의 그림과 같이 기차의 중앙에서 플래시가 터진 후, 플래시의 빛이 기차의 왼쪽 끝과 오른쪽 끝에 있는 거울에 반사되어 돌아오는 경우를 살펴보자.
[그림] 기차의 중앙에서 출발한 빛이 기차의 왼쪽 끝과 오른쪽 끝에 있는 거울에 반사되어 돌아오는 모습의 세계선(점선)
위의 그림은 기차의 중앙에서 출발한 빛이 기차의 왼쪽 끝과 오른쪽 끝에 있는 거울에 반사되어 돌아오는 모습의 세계선이란다. 정지된 기차에서는, 중앙에서 출발한 빛이 동시에 양쪽 거울에 도달한다고 생각하지만, 움직이고 있는 기차를 보면 왼쪽 거울에 먼저 빛이 닿고, 나중에 오른쪽 거울에 빛이 닿게 되지.
이 이야기를 조금만 응용하면 재미있는 이야기가 된단다.
빠르게 날아가는 우주선의 정중앙에서 우주선의 앞뒤로 빛을 보냈다. 빛이 앞(B)이나 뒤(A)에 도달하면 폭죽이 터지도록 장치를 해 두었다. 그러면 폭죽은 동시에 터질까?
답변하기 어려우면, 위의 예에서 거울 뒤에 폭죽을 넣어 놓고 빛이 도달하면 폭죽이 터진다고 생각해봐.
우주선 안의 사람에게는 우주선이 정지해 있는 것으로 보이므로, 위의 왼쪽 그림에 해당하지. 따라서 우주선 안의 사람은 앞(B)과 뒤(A)의 폭죽이 동시에 터지는 것을 보겠지. 하지만 우주선 밖에 있는 사람에게는 우주선이 움직이고 있으므로, 위의 오른쪽 그림에 해당하지. 따라서 우주선 밖에 있는 사람은 뒤(A)의 폭죽이 먼저 터지고, 앞(B)의 폭죽이 나중에 터지는 것을 볼 수 있단다. 말이 안 되는 것 같지만, 사실이란다.
이제 한 걸음 더 나아가 위의 기차 그림에, 시간에 대한 눈금을 넣어보자.
[그림] 시간에 대한 눈금을 넣은 그림
먼저 이 눈금선을 보면, 어떤 사건이 같은 시간에 일어났는지를 좀더 명확하게 알 수 있지. 예를 들어 0.1초 눈금선 위에 있는 A'와 B'는 같은 시간에 일어났다는 것을 알 수 있지. 즉 하나의 눈금선과 여러 개의 세계선이 교차하는 점(사건)들은 모두 같은 시간에 일어났다는 것을 알 수 있지. 이제부터 편리성을 위해 이러한 눈금선을 '동시눈금선'이라 부르자.(동시눈금선은 내가 지어 낸 말이야.)
물론, 동시라는 말은 정지해 있는 사람(철로 변에 서 있는 사람)에게 같은 시간이라는 뜻이란다. 위의 오른쪽 그림을 보면, A'와 B'는 동시에 일어나지 않았는데, 이는 정지해 있는 사람이 볼 때 그렇다는 이야기일 뿐, 움직이는 사람(기차 안에 있는 사람)에게는 A'와 B'가 동시에 일어난 사건이란다. 왜냐하면, 기차 안에 있는 사람이 볼 때에는, 기차 중앙(M)에서 출발한 빛이 동시에 뒤쪽 거울(B')과 앞쪽 거울(A')에 도달하기 때문이지.
그럼 이번에는 움직이는 사람(기차 안에 있는 사람)의 관점에서 보는 동시눈금선을 그려보자. 아래 그림은 움직이는 사람의 관점에서 본 동시눈금선이란다.
[그림] 왼쪽으로 움직이는 사람(기차 안에 있는 사람)의 관점에서 보는 동시눈금선
위의 그림에서 보듯이, 움직이는 사람(기차 안에 있는 사람)의 관점에서 보는 동시눈금선은 A'와 B'를 잇는 선이 된단다. 왜냐하면 움직이는 사람의 관점에서는 A'와 B'가 동시에 일어났기 때문이지. 이와 같이 움직이는 사람의 동시눈금선은 경사지게 보인단다.
만약 기차가 오른쪽으로 움직이지 않고 왼쪽으로 움직인다면, 움직이는 사람(기차 안에 있는 사람)의 관점에서는 보는 동시눈금선은 다음과 같단다.
[그림] 왼쪽으로 움직이는 기차 안의 사람의 관점에서 보는 동시눈금선
지금까지 본 바를 정리하면 다음과 같단다.
- 사람에 따라 서로 다른 동시눈금선을 가지고 있다.
- 동시눈금선은 세계선과 같은 방향으로 기울어져 있다.
■ 쌍둥이 역설과 시간의 지연
이제 세계선과 동시눈금선에 대해 이해를 했으면, 등속 운동만 있는 쌍둥이 역설에 대해 한번 살펴보자.
[그림] 형과 동생이 탄 우주선이 등속 운동을 하면 서로 반대 방향으로 가고 있다.
앞에서 이야기했듯이, 20살에 우주선을 타고 출발한 형과 동생은 40년 후 각자 환갑잔치를 하게 되는데, 각각은 자신이 먼저 환갑잔치를 하고 한참 후 상대방이 환갑잔치를 하는 것을 볼 수 있다고 하였지. 그 이유는 각자마다 서로 다른 동시눈금선을 가지고 있기 때문이란다.
이런 상황을 설명하기 위해 먼저 세계선을 그려보자.
[그림] 형의 관점에서 본 동시눈금선
위의 그림은 형과 동생, 그리고 출발선에 서 있는 사람의 세계선 위에, 형이 본 동시눈금선을 그려 놓았다.(동시눈금선을 그리는 방법은 위의 기차 예에서 이미 설명한 방법대로 그리면 된단다.)
출발한지 40년이 지난 형은 A점에서 환갑 잔치를 하게 되겠지. A와 A'는 동시이니까, 형이 동생을 본다면 동생은 자신보다 젊어 보이겠지. 만약 동생이 B'점에서 환갑 잔치를 한다면, 형은 46년 후인 B점에서 환갑 잔치를 보게 되겠지.
더 나아가, 20살인 형제가 40년 후 형이 먼저 환갑 잔치를 하고, 46년 후 동생이 환갑잔치를 한다는 사실에서 형의 시간보다 동생의 시간이 더 느리게 간다는 사실을 유추할 수 있겠지. 실제로 위의 그림에서 선분 AB에 대한 선분 A'B'의 비율을 계산해 보면, 시간이 느리게 가는 비율을 계산할 수 있단다.
이번에는 동생이 본 동시눈금선을 그려보자.
[그림] 동생의 관점에서 본 동시눈금선
위의 그림은 동생이 본 동시눈금선을 그려 놓았다. 그림을 보면, 동생은 출발한지 40년이 지난 A점에서 환갑 잔치를 하게 되겠지. A와 A'는 동시이니까, 동생이 형을 본다면 형은 자신보다 젊어 보이겠지. 만약 형이 B'점에서 환갑 잔치를 한다면, 동생은 46년 후인 B점에서 환갑 잔치를 보게 되겠지.
더 나아가, 20살인 형제가 40년 후 동생이 먼저 환갑 잔치를 하고, 46년 후에 형이 환갑잔치를 한다는 사실에서 동생의 시간보다 형의 시간이 더 느리게 간다는 사실을 유추할 수 있단다.
위의 이야기를 요약하면, 각각은 자신이 먼저 환갑잔치를 하고 6년 후 상대방이 환갑잔치를 하는 것을 보게 되고, 더 나아가 자신의 시간보다 상대방의 시간이 더 느리게 간다는 것을 알 수 있겠지. 지금까지 우리가 아는 상식으로는, 이러한 사실이 모순처럼 보이지만, 각자마다 서로 다른 동시눈금선을 가지고 있기 때문에(즉 각자마다 다른 시간을 가지고 있기 때문에) 모순이라고 할 수 없단다.
■ 길이에 대한 정의
서울에서 부산으로 달려가는 기차가 있다. 지금 달려가는 기차의 길이를 재려고 한다고 하자. 만약 정지해 있는 기차라면 긴 줄자를 들고 가서 기차의 길이를 재면 되지만, 달리는 기차는 그렇게 하기가 힘들다. 그래서 나는 다음과 같은 방법으로 기차의 길이를 재었단다.
"먼저 2개의 막대를 준비한다. 그리고 두 명이 철로 둑에 서 있다가 기차가 지나갈 때, 한 명은 기차의 맨 앞 부분이 지나가는 자리에, 다른 한 명은 맨 뒤 부분이 지나가는 자리에 막대를 땅에 꽂는다. 그리고 나서 두 막대 사이의 거리를 줄자로 재어 기차의 길이를 잰다."
[그림] 기차가 지나갈 때, 기차의 앞과 뒤에서 막대를 꽂는 모습
아마도 이렇게 해서 기차의 길이를 재면 움직이는 기차의 길이를 알 수 있겠지. 그런데 하나 주의할 점이 있단다. 두 막대를 땅에 꼽을 때 반드시 '동시'에 꽂아야 한다는 것이지. 만약 아래의 이야기와 같이 두 막대를 꽂는 시간에 차이가 있다면 길이가 올바르다고 할 수 없겠지.
"기차가 서울에서 출발할 때 기차의 맨 뒤 부분에 막대를 하나 꼽고, 기차가 부산에 도착할 때 쯤 기차의 맨 앞 부분에 막대를 하나 꼽은 다음, 두 막대의 거리를 재어 기차의 길이를 구하였다."
이 이야기를 들어보면, 두 막대를 '동시'에 꼽아야만 하는 이유를 이해할 수 있겠지. 길이를 정의하는 방법에 대한 이야기가 좀 길어졌지만, 요약하면 다음과 같단다.
"물체의 길이는 '동시'에 앞 부분과 뒤 부분의 위치를 구한 다음, 두 위치의 거리를 구하면 된다."
너무나 쉽고도 당연한 이야기를 길게 해서 미안하지만, 문제는 지금부터란다. '동시'에 막대를 꽂아야 하는데, 지금까지 봐왔듯이, 움직이는 사람이 볼 때의 '동시'와 정지해 있는 사람이 볼 때의 '동시'는 다르기 때문이지. 그리고 정지한 사람이 움직이는 물체를 볼 때 길이가 짧아지는 이유가 여기에 있단다.
자! '동시'라는 말에 유의하면서 아래의 그림을 한 번 보자.
[그림] 기차의 중앙에서 출발한 빛이 기차의 왼쪽 끝과 오른쪽 끝에 있는 거울에 반사되어 돌아오는 모습의 세계선(점선)
이 그림은 동시성을 설명하기 위해 위에서 나왔던 그림이란다. 이 그림에서 3개의 세계선은 각각 기차의 맨 뒤 부분, 중앙 부분, 맨 앞 부분을 나타내고 있지. 길이의 정의에 따르면, 맨 뒤 부분과 맨 앞 부분의 위치를 동시에 측정하여 그 거리를 구하면 기차의 길이가 나오겠지. 따라서 위의 그림에 나오는 3대의 기차는 모두 정지한 사람의 입장에서 본 기차의 길이란다. 즉, 기차의 시작점과 끝점의 위치가 모두 정지한 사람의 동시눈금선(수평선) 위에 위치하고 있기 때문이지.(앞에서도 이야기했듯이, 정지한 기차(왼쪽 그림의 기차)의 길이보다 움직이는 기차(오른쪽 그림의 기차)의 길이가 짧아진단다. 하지만, 여기에서는 실제 길이를 무시하자. 다만 길이를 재는 방법에만 집중하자. 길이가 짧아지는 이유에 대해서는 아래에서 자세하게 설명할 예정이야.)
이제, 움직이는 사람(기차 안의 사람)의 동시눈금선은 정지한 사람(철로 변에 있는 사람)의 동시눈금선과 다르다는 사실에 유의하면서 아래 그림을 한번 살펴보자.
[그림] 움직이는 사람(기차 안에 있는 사람)의 관점에서 본 기차의 길이
움직이는 사람의 관점에서 기차의 길이를 구하려면, 위 그림에서 A'와 B'간의 거리가 기차의 길이가 된단다. 왜냐하면, 두 점 간의 거리를 구하기 위해서는 두 점의 위치를 동시에 측정하여야 하는데, A'와 B'는 움직이는 사람의 동시눈금선에 위에 있기 때문에 '동시'라고 볼 수 있기 때문이지.
■ 길이의 축소
이제 움직이는 물체의 길이는 짧아져 보이는 이유를 살펴보자. 아래의 그림은 쌍둥이 형과 동생이 탄 우주선의 세계선이란다.
[그림] 형의 관점(형이 정지)에서 본 우주선의 길이
각각의 우주선은 2개의 세계선이 있는데, 하나는 우주선의 꼬리(맨 뒤) 부분, 다른 하나는 우주선의 머리(맨 앞) 부분의 세계선이란다. 우주선의 길이는 이 두 세계선 사이의 거리가 되겠지. 먼저 형의 동시눈금선을 기준으로 우주선의 길이를 살펴보자. 그림을 보면 동시눈금선과 형 우주선의 세계선이 만나는 점 A와 B간의 거리는 형 우주선의 길이가 되겠지. 또, 점 A'와 B'간의 거리는 형이 본 동생 우주선의 길이가 되겠지.
그림을 보면 동생 우주선의 길이(선분 A'B')가 형 우주선의 길이(선분 AB)보다 짧다는 것을 한눈에 알 수 있지. 즉, 형의 관점에서는 동생 우주선이 자신의 우주선보다 짧게 보이겠지. 형의 관점이란 이야기는 자신은 정지하고 동생이 움직이고 있다는 가정이 들어가 있지. 따라서 움직이는 물체의 길이는 축소되어 보인다고 할 수 있겠지. 그리고 선분 AB에 대한 선분 A'B'의 비율이 길이가 축소되는 비율이 된단다.
자 이제 반대로 동생의 관점에서 우주선의 길이를 비교해 보자. 아래의 그림은 동생의 동시눈금선을 그려 놓은 그림이란다.
[그림] 동생의 관점(동생이 정지)에서 본 우주선의 길이
이때 점 A와 B간의 거리는 동생 우주선의 길이가 되고, 점 A'와 B'간의 거리는 형 우주선의 길이가 되겠지.
그림을 보면 형 우주선의 길이가 동생 우주선의 길이보다 짧다는 것을 한 눈에 알 수 있지. 즉, 동생의 관점에서는 형 우주선이 자신의 우주선보다 짧게 보이겠지. 동생의 관점이란 이야기는 자신은 정지하고 형이 움직이고 있다는 가정이 들어가 있지. 따라서 움직이는 물체의 길이는 축소되어 보인다고 할 수 있겠지.
이로서 움직이는 물체의 길이가 축소되는 이유를 살펴보았단다.
■ 문제
마지막으로 네 교과서에 나오는 문제 하나만 풀어보고 끝내도록 하자.
길이가 같은 두 우주선을 형과 동생이 타고 서로 반대 방향으로 같은 속력으로 스치듯이 지나가고 있다. 동생의 우주선의 뒤 부분이 형의 우주선의 앞 부분을 막 지나가고 있을 때, 형의 우주선 뒤 부분에서 총을 발사했다. 이때 총알이 동생의 우주선에 맞았을까 아니면 맞지 않았을까?
[그림] 형 우주선의 머리(맨 앞) 부분이 동생 우주선의 꼬리(맨 뒤) 부분을 막 지나가고 있는 모습
위의 그림을 보면, 형의 우주선의 머리(맨 앞) 부분과 동생의 우주선의 꼬리(맨 뒤) 부분이 일치하는 경우는 2가지가 있을 수 있다. 왼쪽 그림은 형의 관점에서 동생의 우주선을 보았을 때이다. 형의 관점에서 보면, 동생의 우주선은 길이가 짧아져서, 총에 맞지 않는다. 하지만 동생의 관점에서 보면, 오른쪽 그림과 같이 형의 우주선은 길이가 짧아지기 때문에 총에 맞게 된다. 이 둘은 분명 모순이 있어 보인다. 그렇다면, 실제 상황에서는 총에 맞을까 맞지 않을까?
여기에 대한 답변을 하기 위해서, 먼저 동생 우주선과 형 우주선의 세계선을 아래와 같이 그려보자. 이때 동생의 세계선은 지면 앞으로 약간 튀어 나와 있다고 가정하면, 두 우주선은 충돌하지 않고 스쳐 지나가겠지.
[그림] 형의 동시눈금선으로 두 우주선을 볼 때. 점 B에서 총을 발사.
이제 형의 관점에서 동시눈금선을 보자. 위의 그림에는 두 개의 화살표가 있는데, 실선 화살표는 형의 우주선, 점선 화살표는 동생의 우주선이란다. 또, 화살촉이 있는 쪽이 우주선의 머리 부분이란다. 점 A에서 형 우주선의 머리(맨 앞) 부분과 동생 우주선의 꼬리(맨 뒤) 부분이 일치하고 있단다. 이와 동시에, 점 B(형 우주선의 꼬리 부분)에서 총을 발사하더라도, 동생의 우주선이 점 B에 도달하지 않았기 때문에 총에 맞지 않겠지.
이제 동생의 관점에서 보자.
[그림] 동생의 동시눈금선으로 두 우주선을 볼 때. 점 B에서 총을 발사.
위의 그림을 보면, 형의 관점에서는 점 A(우주선의 일치)와 점 B(총 발사)가 동시에 일어난 사건이지만, 동생의 관점에서는 점 B(총 발사)가 먼저 일어나고, 점 A(우주선의 일치)가 나중에 일어난 사건이란다. 또 동생의 관점에서는 형이 점 B에서 총을 발사할 때, 자신의 우주선은 점 B에 도달하지 않음을 알 수 있다. 따라서 동생의 우주선은 총에 맞지 않겠지.
요약하면, 형의 관점에서나 동생의 관점에서나, 동생의 우주선은 총에 맞지 않는단다.
이 문제에서 하고자 하는 이야기는, 형에게 동시에 일어난 사건(우주선의 일치와 총의 발사)이, 동생에게는 동시에 일어나지 않는다(총이 먼저 발사되고, 나중에 우주선이 일치함)는 사실이란다. 더 나아가 사람마다 제각기 다른 시간을 가지고 있다는 사실을 강조하기 위함이란다.
위의 문제를 응용하면, 다음과 같은 문제가 될 수 있다.
아래의 그림처럼, 동생의 자동차가 오른쪽에서 왼쪽으로 빛의 속도에 가까운 속도로 달리면서 형의 차고를 지나가고 있다. 자동차의 길이와 차고의 길이는 똑같고, 차고의 왼쪽 문과 오른쪽 문은 열려 있는데, 동생의 차가 차고에 들어왔을 때 차고의 왼쪽 문과 오른쪽 문은 순간적으로 닫혔다가 열린다고 가정을 하자.
[문제] 형의 차고를 지나가는 동생의 자동차
이 경우, 형의 관점에서 보면(왼쪽 그림), 자동차 길이는 축소되어 보이기 때문에 차고에 들어가는 것이 문제가 없지만, 동생의 관점에서 보면, 차고의 길이가 축소되어 보이기 때문에 차고의 문은 닫히지 않겠지. 과연 자동차는 안전하게 통과할 수 있을까? 아니면 차고 문과 자동차는 부셔질까?
이 문제의 답도 위에 나온 형과 동생의 우주선 문제와 동일하단다. 형의 우주선 대신 형의 차고를, 동생의 우주선 대신 동생의 차를 대입하면 똑같은 문제가 된단다.
형의 관점에서 보면 자동차가 차고에 들어갔을 때 두 문이 동시에 닫히고 열리지만, 동생의 관점에서 보면 동시에 열리고 닫히지 않는단다. 자동차의 앞부분이 차고에 들어갈 때 왼쪽 문이 먼저 닫히고 열린 후에, 자동차의 뒤 부분이 다 들어 간 후 오른쪽 문이 닫히고 열린단다. 따라서 동생 차는 차고를 무사하게 통과하겠지.
그런데 위의 두 가지 문제를 풀 때 주의해야 할 것이 있다. "동시에 총을 발사하였다"나 "동시에 문을 닫았다"는 문장에서 동시라는 말은 형의 관점에서 동시라는 전제를 하고 있단다. 만약 동생의 관점에서 동시라는 말을 사용한다면, 반대 상황이 일어난단다.
민코프스키의 세계선은 이외에도 여러 가지 경우를 설명하는데 매우 유용하지만, 이쯤에서 이야기를 마치도록 하자.
쌍둥이 역설에서 하나 더 알아야 하는 사실은, 형이 볼 때에는 형의 환갑잔치 → 동생의 환갑잔치 순으로 보이고, 동생이 볼 때에는 동생의 환갑잔치 → 형의 환갑잔치 순으로 보인다고 해서, 하나의 사건에서 원인과 결과가 뒤바뀌어 보이는 일은 절대 일어나지 않는다는 것이야. 예를 들어, 형이 씨를 뿌려 새싹에 났는데, 동생에게는 새싹부터 보이고 나중에 형이 씨를 뿌리는 모습을 보는 일은 절대 일어나지 않는단다. 즉 결과는 항상 원인보다 나중에 보인단다.
철학에서는 이것을 인과율(因果律)이라고 부르는데, '모든 일은, 원인(原因)에서 발생한 결과(結果)이며, 원인이 없이는 아무것도 생기지 아니한다'는 법칙이란다.






















