산술 기하, 조화 평균정리

[유토피아]

산술평균 기하평균, 조화평균의 의미

1 . 산술적 증명

한큐에 이해하는 산술평균 기하평균

http://cafe.naver.com/suhui/13751323

2. 도형의 형태를 통한 이해 

우선 산술평균은 너무나 잘 알고 계시리라고 생각됩니다.
우리가 일상생활에서 사용하는 평균, 점수를 계산하고 물건을 나누고.. 하는데 사용하는
평균이 바로 산술평균입니다.
간단하게 수학 시험이 있을때 5명이 봤다고 하면
100점 90점 100점 80점 30점 이라고 합시다.
그러면 이 시험의 평균점수는 60점이 됩니다. 즉 (a+b+c+d+e)/5 를 말합니다.
너무나 익숙한 개념이라 별다른 설명이 필요없을듯 합니다.

그럼 기하평균에 대해서 설명을 드리자면 기하평균은 Geometric mean 이라고 하지요.
단어에서 바로 감이 오지요? 기하학적인 평균을 말합니다.
머리속에 그림을 그리세요.
예를 들어 사각형이 있다고 합시다. 각 변의 길이를 12, 3 이라고 합시다.
그럼 그 넓이는 36이 되지요?
그럼 그 전에 그 변의 길이는 잊어버리시고 넓이 36이 되게 하는 변의 길이는 무엇일까요?
꽤 많이 있지요?? (1,36) , (2,18)~~~~~~~,(6.6),~~~~~~~(36,1) <<-- 정수만을 생각합니다.
그중에서 기하학적인 평균치는 무엇일까요? (1,36) 은 아니겠지요.
즉 한변의 길이가 6일때 그 6이 바로 넓이 36이 되게 하는 기하학적인 평균치가 됩니다.

변수가 3개라면 입체를 떠올리시면 됩니다. 직육면체의 부피를 생각할때 기하학적인 평균은 3변의 길이가 모두 같을 때 그 변의 길이가 기하평균이 됩니다.

항이 4개라면 어떻게 될까요?? 변이 3개까지는 3차원공간에서 머리속에 그림이 떠오르니 쉽게 할수 있지만 변이 4개가 되면 달라집니다. 그림이 그려지지가 않지요. 4차원을 그리는 것은 불가능합니다.

하지만 3차원까지의 논의를 바탕으로 그 개념을 확장할순 있습니다.
n개의 변수의 기하평균은 n개의 수를 모두 곱한후에 n 제곱근을 구하면 됩니다.

3. 생활속의 상식을 통한 이해

어떤 가정에서 매주 쇠고기와 생선을 사먹는데 똑같은 돈을 지출했는데, 일주일 사이에 쇠고기 가격이 2배로 뛰었을 때 지난주와 똑같은 양을 샀다면 지출금액은 50% 증가하는 것이 산술평균

즉, (10,000원+10,000원)/2=10,000원 => (10,000원+20,000원)/2=15,000원?

?

그런데, 쇠고기와 생선에 똑같은 금액을 지출한다면...기하평균을 사용해야 한다.

즉 곱의 평균을 사용해야 하므로 기하평균을 쓴다는 말이다.

증가분의 중간값을 서로 곱해줘야 중간값이 나온다

√20,000/10,000 x √10,000/10,000 = 1.414 ?

지출금액은 41.4% 증가한다.?

조화평균harmonic mean , 調和平均

n개의 측정치 또는 통계학적 자료가 있을 때, 이들의 역수에 대한 산술평균을 구하고, 이를 역수로 나타낸 것이다. 즉, n개의 자료인 b₁, b₂,…, b_n이 있을때, 이들의 역수인 1/b₁, 1/b₂, …, 1/b_n을 먼저 구하고, 이들의 산술평균을 구한 뒤 다시 역수로 나타내는 것이다. 집단의 평균 사례수를 말하며 불균형 자료의 경우 극단치를 줄여 균형자료로 만들기 위한 방법으로 사용되며 가속 현상에서의 평균 시속을 구할 때도 조화평균이 사용된다.

실제로 조화평균의 사례를 적용해보자!

내진설계시 지반등급의 결정을 위해 상부 30m 지반 특성을 조사하게 됩니다. 이 때 '조화 평균'을 사용하게 되는데 왜 조화평균을 사용해야 하는지 아래의 설명을 보면 알 수 있을 것 같습니다. 아래의 설명은 네이버 백과사전 내용입니다. 아래의 첫번 째 예로 평균 속도를 계산해보면 조화평균 식이 유도되네요.^^

----------------------------------------------------------

n개의 양수 a₁,a₂,…,a_n에 대하여 그 역수 1/a₁, 1/a₂, …, 1/a_n을 산술평균한 것의 역수. 즉, 조화평균을 H라 하면,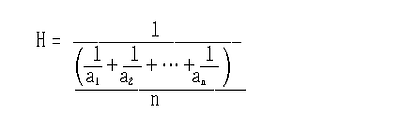

이 된다. 두 지점 A,B를 갈 때는 a km/h의 속도로, 올 때는 b km/h의 속도로 왕복했다면 이 사람의 평균속도는 a와 b의 조화평균에 해당된다. 또 100 m를 뛰는 데 3회 뛴 시간이 a초, b초, c초였다고 하면, 그 평균은 a,b,c의 조화평균으로 구해진다. 이와 같이 일이나 능률의 예에서는 산술평균기하평균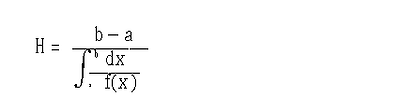

로 구하는 경우도 있다

-------------------------------------------------------------------

산술평균 기하평균 조화평균값 구하기

산술,기하,조화 평균은 항이 n개일때도 성립하는데 여기서는 항이 2개일때만 증명해보겠습니다.  단 a,b는 양수인 실수입니다!!

 

여기서

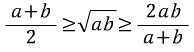 가 성립한다. 

Section 1 - 유래

1. 산술평균

우리 시험점수 평균이 몇이다 하죠? 우리가 흔히 말하는 "평균" 입니다.

즉 다시말하면 변량수만큼을 곱해서 변량의 합이 되는 수이죠!

이수는 딱히 유래를 설명할건 없네요!!

2. 기하평균

일치하지 않는 두직선에서 위 그림과 같을 때(저 D,E,F는 접점)

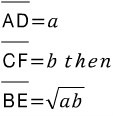
가 성립한다.

Proof)

   

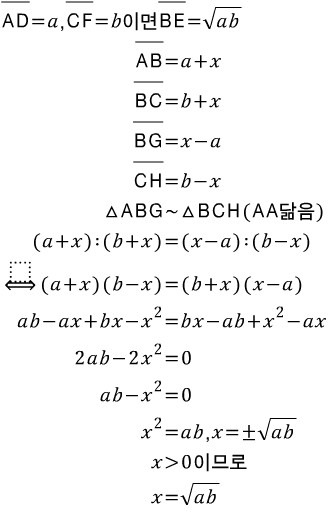
이제   조화평균에 관하여 알아봅시다.

피타고라스 아시죠??

무리수의 존재를 알고있었고, 이를 누설한 사람을 바다에 빠뜨려 죽이고, 피타고라스의 정리를 발견하고

철학자에 수학자에 할껀 다해본 할짓 없던 아저씨..

이 아저씨가 음악도 했었는데요. 아래 그림을 보시죠 ㅋ

길이가 a만큼인 줄을 당길때 C라는 음이 나온다고 가정했을 때

그거에 절반길이를 잡아당기면 같은 C가 나옵니다만, 1옥타브가 높은 음이 나오죠..(a/2 를 편의상 b라고 가정합니다)

그리고 그 두 음과 화음을 이루는 음을 내기위한 줄의 길이가 2ab/(a+b)  가 된다는 것이죠..

그리고 이걸 또 대수적으로 표현해서 조화평균을 만듭니다 ㅡ_ㅡ...

또한 저게 b가 꼭 a/2 가 아니라도 성립한다네요;;

근데 현대 음악에서 저게 거의 맞다고 합니다. 오차가있지만요 ㄷㄷ..

정말 대단한 아저씨입니다 ㄷㄷ

서론이 좀 길었습니당~ 이제 간단하게 증명을 해보고 마치도록할게요!!

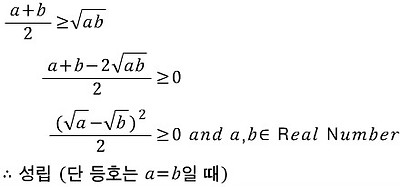
이제 기하평균이 조화평균보다 크거나 같다를 증명해보겠습니다.

따라서

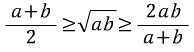가 성립한다.