룩스진의 역사유람 Lux Jin’s Histoy tour
대칭성 (symmetry): 뇌터의 정리
대칭 성 (symmetry)
원자나 분자와 같은 입자들이 어떤 축을 중심으로 일정한 각도로 회전시키거나 거울면을 통해 반사시키는 대칭조작을 해도 그 성질이 변하지 않는다는 물리개념.
물리학에 대칭의 개념을 적용시켜 보면 특정한 물리법칙, 예를 들면 보존법칙인 경우 대상입자의 좌표(4차원을 고려할 때는 시간도 포함됨)에 대칭조작을 해도 영향을 받지 않는다는 중요한 결론을 얻을 수 있다. 즉 이 법칙은 우주의 모든 시간과 공간에서 성립한다는 것이다. 입자물리학에서는 대칭성을 이용하여 보존법칙을 유도해낼 수도 있고, 입자들 간의 상호작용중 일어날 수 있는 것과 그렇지 못한 것(즉 '금지'되었다고 하는 것)을 결정할 수 있다. 그밖의 여러 물리학·화학 분야에서 대칭성이 이용된다.
관련된 분야로 상대론·양자론·결정학·분광학 등을 들 수 있다. 결정이나 분자는 가능한 대칭조작의 종류나 개수로 기술할 수 있다. 대칭조작을 정량적으로 다루는 학문을 군론이라 한다. 이때 유효 대칭조작이란 대칭조작을 해도 물체의 모양이 변하지 않는 것을 말한다. 이 조작의 종류나 개수는 조작을 할 물체의 기하학적인 모양에 따라 다르다.
예를 들어 탁자 위의 정4각형을 가지고 대칭조작이란 무엇이고 어떤 종류가 있는지 설명할 수 있다. 이 정4각형에 있어서 유효 대칭조작으로는 4각형의 정가운데를 중심으로 90°, 180°, 270°, 360° 회전시키는 것, 마주보는 두 꼭지점이나 변의 중점을 지나고 탁자에 수직한 거울면을 통한 반사, 탁자면에 놓여 있는 거울면을 통한 반사 등이 있다. 이렇게 해서 원래의 정4각형과 똑같은 모양을 만들어내는 대칭조작은 9가지가 있다. 그러나 원일 경우는 더욱 대칭성이 높아서 90°의 정수배뿐만 아니라 임의의 어떤 각도로 회전시켜도 그 모양에 변화가 없다.
원자구성입자는 다양한 특성을 가지며 대칭성을 갖는 힘에 영향을 받는다. 이러한 특성 가운데 하나로서 반전성보존법칙을 낳는 반전성(parity)이 있다. 양자역학에서는 모든 소립자나 원자를 파동방정식으로 표현할 수 있다. 만약 이 입자의 모든 공간좌표를 원점에 대해 동시에 반전시켜도 그 파동방정식이 변하지 않는다면 이 입자는 우반전성(even parity)을 가진다고 하며, 그와는 달리 원래의 파동방정식과 부호만 다르다면 기반전성(odd parity)을 가졌다고 한다.
분자와 같이 여러 입자들이 모였을 때도 전체의 공간반전성은 시간에 따른 물리적 과정이나 상호작용에서 변하지 않는다. 이러한 성질을 공간반전성 보존법칙으로 설명할 수 있다. 입자의 또다른 특성 중에는 스핀이나 입자의 고유 각운동량이 있다. 원자 내부의 전자는 양자화된 에너지 준위를 가질 뿐만 아니라, '위' 또는 '아래'로 향하는 양자화된 스핀도 있다. 스핀 각운동량은 보존된다고 알려져 있다. 만약 분자를 구성하는 모든 전자의 스핀 방향이 동시에 반전된다고 해도 그 분자의 성질은 변함이 없다.
소립자들은 내부 대칭성을 가졌다고 할 수 있는데, 이러한 대칭성은 특히 입자들을 분류하고, 선택법칙(selection rules)을 유도할 때 편리하다. 이러한 내부대칭성을 중입자수(baryon number)라고 하며, 이들 입자들은 강입자(hadron)라고 한다. 중입자수가 0인 입자들은 중간자(mesons)라 하고, +1인 것을 중입자라고 한다. 대칭성에 따라 중입자수가 -1인 입자도 존재하며, 반중입자라 한다. 이러한 중입자수는 핵의 상호작용 중에도 보존된다.
---------------------------------------------------------
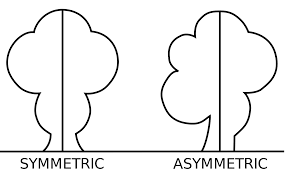
물리학에서 대칭 성은 매우 중요한 역할을 한다.
예를 들어 원의 경우 어떤 각도로 회전을 시켜도 모양은 변하지 않는다.
이 것이 대칭 성이다.
뇌터의 정리 (Noether's theorem)
어떤 물리 계의 속성에 연속적인 대칭 성을 갖는다면 보존 된 값의 양은 같을 것이다.
대칭성 ↔ 보존 법칙
| 회전 대칭성 | 각 운동량 보존 | 시간 병진 대칭성 | 에너지 보존 | 공간 병진 대칭성 | 운동량 보존 | 양자 역학 대칭성 | 전하 |
왜 뇌터의 정리가 매우 중요한가???
보존 법칙이 대칭 성에서 온 것을 증명했기 때문이다.
에미 뇌터 (Emmy Noether; 1882 ~ 1935)
에미 뇌터는 독일 바이에른 주 에를랑겐에서 태어났고 아버지 막스 뇌터는 유태인이며 대수기하학자로 에를랑겐 대학에 수학 교수로 재직하고 있었다. 에미는 영어와 불어를 가르치기 위한 자격증을 획득했지만 수학에 흥미를 느껴 1904년 에를랑겐 대학에서 수학을 공부하기 시작했고 1907년 논문 제출 후 입학 3년 만에 박사 학위를 받았다. 이 논문으로 서서히 그녀의 이름이 알려지기 시작했다. 하지만 에미는 여자라는 이유로 교수 직위는 커녕 보수조차 받지 못하고 에를랑겐 대학에서 수학을 가르쳤다.
1915년경 아인슈타인은 일반 상대성이론에 대한 마지막 손질을 보고 있었고 괴팅겐 대학의 힐베르트 (David Hilbert)와 Felix Klein은 일반 상대성 이론에서 에너지가 보존 되지 않는 문제 점에 대해 고민하고 있었다.
만약 에너지가 시공간을 휘게 하고 시공간은 에너지를 포함하고 있다면 시공간이 시공간을 포함한다는 역설이 된다.
힐베르트는 에미 뇌터가 이 문제를 해결할 수 있을 것이라 생각해 괴팅겐 대학에의 교수로 초대하자 여자라는 이유로 동료들이 반대했다. 힐베르트는 "그녀를 대학에서 가르치도록 해야 한다. 이곳은 교수단이지 탈의실이 아니다."라며 동료들을 설득했고 그 결과 힐베르트 조교로 강의할 수 있었다. 비록 그녀는 보수도 받지 못하고 대학에서 가르쳤지만 놀라울 만한 업적인 뇌터의 정리를 발표했다. 이 정리가 없었다면 아마도 일반 상대성이론은 끝내지 못했을 지도 모른다. 설상가상으로 당시 나찌즘으로 인해 유태인이었던 뇌터는 괴팅겐 대학에서 추방되었고 독일을 떠나야만 했다. 그녀는 미국으로 건너가 대학 강단에 섰지만 얼마지 않아 종양 제거 수술 후 사망했다.


연속 대칭 성 (continuous symmetry)
- 회전 대칭 성 (rotational symmetry): 어떤 물체를 회전 시켰을 때 그 물체가 변하지 않는 것을 회전 대칭 성이라고 한다. 예를 들어 수소 원자는 회전을 해도 같은 수소 원자이다.
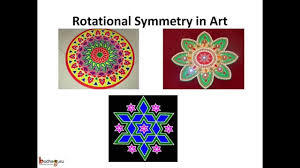
이 패턴은 회전을 시켜도 같은 패턴을 갖고 있는데 이것을 회전 대칭 성이라고 한다.
- 병진 대칭 성 (translational symmetry: 공간 병진 대칭성, 시간 병진 대칭성) - 회전이나 반사가 아닌 시간 혹은 공간의 변환에도 그 물리 계가 변하지 않는 것을 말한다. 예를 들어 어떤 에너지를 가진 입자가 공간을 달리해도 입자의 에너지는 변하지 않는다.
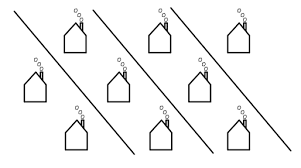
이 패턴은 좌우, 상하, 앞뒤 등 거리의 변환에도 같은 패턴을 갖고 있는데 이것을 병진 대칭 성이라고 한다.
---------------------------------------------------------
룩스진의 역사유람 Lux Jin’s Histoy tour
구독자 191명
구독
질점의 운동법칙을 누가 강체의 운동법칙으로 확대했고, 운동량 보존법칙과 면적속도가 어떤 관계인지, 극좌표에서 r 방향 가속도와 phi 방향 가속도를 어떻게 유도할 수 있는지, phi 방향 가속도에 각운동량 보존 법칙이 어떻게 숨어있는지, 20세기 독일 수학자 Noether 가 이러한 보존법칙을 어떻게 통찰했는지 알아보기 위해 여행을 떠납니다. To see who extended the laws of motion from the points of mass to the rigid bodies, what is the relationship between the conservation of momentum and the areal velocity, how the r-direction acceleration and the phi-direction acceleration can be derived in the polar coordinates, how the angular momentum conservation law is hidden behind the phi-direction acceleration, how German mathematician Noether had the insight into these laws of conservation in the 20th-century, let's go on a trip. 케플러, 보존, 뇌터, Kepler, conservation, Noether, 케플러의 법칙, 각운동량 보존 법칙, 뇌터의 정리, 면적속도, Kepler's Law, conservation of Angular Momentum, Noether's Theorem, areal velocity, 티코 브라헤, 태양, 초점, 타원, 뉴턴, 질점, 만유인력, 관성, 힘, 작용과 반작용, 프린키피아, 운동량 보존법칙, 오일러, 메카니카, 강체, ellipse, Newton, mass, universal gravitation, inertia, force, Principia, conservation of momentum, Euler, Mechanica, rigid body, 극좌표, 위치 벡터, 단위벡터, 가속도, 변위, 회전, 라그랑지안, 공간, 대칭성, polar coordinates, unit vector, acceleration, translation, rotation, Lagrangian, space, symmetry, [Eng Sub]Trip4. 천체의 운동 원뿔곡선, celestial motion conic section [Lux Jin's] https://youtu.be/bDmUwoQBI1k Trip 5. 만유인력과 뉴턴의 운동법칙 universal gravitation and Newton's laws of motion https://youtu.be/pXJ48XLBEWw Trip 6. 원운동의 비밀 가짜힘 secret of the circular motion, fictitious force https://youtu.be/QkPCRt1Fjm8 7. 원운동 가속도 유도derivation of the acceleration in the circular motion https://youtu.be/txRc6Aefugo 8. 중력질량, 관성질량, 등가원리, 일반상대성 [룩스진의 역사유람 Lux Jin's] gravitational mass, inertial mass, and equivalence principle[Lux Jin's] https://youtu.be/1f0XlIsS0YM 9. 상대성이론 질량의 소개와 유도 Introduction to relativistic mass with its derivation[룩스진의 역사유람 Lux Jin's] https://youtu.be/fTB9N-Zd1cM 10. 질량-에너지 등가의 발견 discovery of mass-energy equivalence[룩스진의 역사유람 Lux Jin's] https://youtu.be/kYQ4FD8iKBw 11. 힘, 일, 에너지, 역학적에너지 보존 force, work, energy, and mechanical energy[룩스진의 역사유람 Lux Jin's] https://youtu.be/HYmpUTrUAQs 12. 지레의 원리와 에너지 보존법칙 principle of lever and law of energy conservation[룩스진의 역사유람 Lux Jin's] https://youtu.be/R901qXaRvlg 13. 지레와 도르래, 에너지 보존, 등가원리 levers and pulleys, energy conservation, equivalence principle[룩스진의 역사유람 Lux Jin's] https://youtu.be/ahw9AQ4jSNA 14. 복합도르래, 에너지, 후크의 법칙, 용수철 진동 pulleys, energy, Hooke’s law and spring cycle[룩스진의 역사유람 Lux Jin's] https://youtu.be/qQ9WD2rd2es 15. 에너지 보존과 운동에너지, 도르래와 용수철 energy conservation and kinetic energy, pulley and spring[룩스진의 역사유람] https://youtu.be/S5n9RjSlE0o 16. 위치에너지의 유도, 케플러 법칙과 에너지 보존 derivation of potential energy, Kepler’s law with energy conservation[룩스진의 역사유람 Lux Jin's] https://youtu.be/JvYGoLYFKYQ 17. 토리첼리, 유체역학, 그리고 에너지 보존법칙 [룩스진의 역사유람 Lux Jin's] Torricelli, fluid mechanics and the law of energy conservation[Lux Jin's] https://youtu.be/Gx1yPfZkcHs 18. 일상생활 속의 파스칼 Pascal in everyday life[룩스진의 역사유람 Lux Jin's] https://youtu.be/SPQC1l7kAsE 19. 파스칼과 에너지 보존 Pascal and energy conservation[룩스진의 역사유람 Lux Jin's] https://youtu.be/-TmWb9A8mzo 20. 아르키메데스의 원리와 파스칼의 법칙 Archimedes’ principle and Pascal’s law[룩스진의 역사유람 Lux Jin's] https://youtu.be/8jZFE2Oxn0w 21. 밀도, 아르키메데스의 원리와 질량보존 Density, Archimedes’ principle and mass conservation[룩스진의 역사유람 Lux Jin's] https://youtu.be/y7SnNf1vzoQ 22. 아르키메데스, 발산정리로 유도한 부력의 원리Archimedes, buoyancy principle with divergence theorem[룩스진의 역사유람] https://youtu.be/WG0kAx2iJaM 23. 헬레니즘 시대의 수학자와 과학자, 알렉산더 대왕의 동서융합 [룩스진의 역사유람 Lux Jin's] https://youtu.be/QcMUaLIy138 24. 유클리드, 평행선 공준과 동치명제, 비유클리드 기하학과 일반상대성[룩스진의 역사유람 Lux Jin's] https://youtu.be/AiqX_uEgMfo 25. 아리스타르코스, 태양과 달까지의 거리비, 그리고 태양중심설[룩스진의 역사유람 Lux Jin's] https://youtu.be/BnsauDfipX0 26. 아르키메데스, 태양중심설 근거, 모래알 개수 어림잡기 Archimedes, heliocentrism based sand reckoner[룩스진의 역사유람 Lux Jin's] https://youtu.be/eNJ1LFTV6rI 27. 아르키메데스, 포물선 조각의 면적, 소진법과 적분결과의 비교 Archimedes, parabolic segment, the method of exhaustion and calculus [룩스진의 역사유람 Lux Jin's] https://youtu.be/700cEXeUKzg 28. 아르키메데스, 포물선 특성, 기하에서 과학으로 Archimedes, parabolic feature, from geometry to science https://youtu.be/Q_Fbnw4yGq8 29. 에라토스테네스, 트로이 전쟁, 에라토스테네스의 체, 지리학의 아버지 Trojan war, sieve of Eratosthenes, father of geography [룩스진의 역사유람 Lux Jin's] https://youtu.be/WpzWcd0ZpW0 30. 아폴로니우스의 원과 천체역학의 원뿔곡선 Circles of Apollonius and the conic section in astrodynamics[룩스진의 역사유람 Lux Jin's] https://youtu.be/PSv0RwKXrXQ 31. 해시계, 당들랭의 구와 원뿔곡선 증명 Sundial, Dandelin sphere and proof of conic section[룩스진의 역사유람 Lux Jin's] https://youtu.be/6dmo9wW2C_c 32. 원뿔곡선의 극좌표 방정식 유도와 표현식의 활용 Derivation of the conic section’s equation and the application [룩스진의 역사유람 Lux Jin's] https://youtu.be/cw7S4JOrXX0 33. 중력장의 에너지, 원뿔곡선, 탈출속도와 블랙홀 Energy, conic section, escape velocity and black hole in gravity[룩스진의 역사유람 Lux Jin's] https://youtu.be/OxzstIxjlCg video clip list 영상모음 https://www.youtube.com/playlist?list... #케플러 #보존 #뇌터 #대칭 #Kepler #conservation #Noether #symmetry