금속에 빛을 쪼일 때 전자가 튀어나오는 현상을 말한다.
1887년 헤르츠는 빛을 쬔 금속에 방전현상이 최저전압을 변화시키는 것을 발견했다.
1900년 레나르트는 빛을 쬘 때 나오는 전하들의 일반성을 보였다.
금속에서 나온 전자로 생긴 전류는 빛의 세기에 비례하고 최대 운동에너지는 진동수에 의존한다는 것이 밝혀져 고전물리학으로 설명되지 않던 빛과 물질 사이의 상호작용을 시사했다.
아인슈타인은 광자가 물질을 투과할 때 원자와 충돌할 것이라고 가정하고 운동에너지를 함수로 표현하였다. 1931년 파울러는 광전류와 온도의 관계를 입증했다.
반도체에서의 광전효과는 양자역학으로만 설명된다.
반도체의 경우 빛의 형태로 에너지를 주어 원자가전자를 전도대로 올려놓을 수 있다.
-----------------------------------------------------------------------
광전효과는 보통 금속 표면에 빛을 쪼였을 때 금속 표면에서 전자가 튀어나오는 현상을 말한다.
넓은 의미로는 복사 에너지가 가시광선·자외선·X선·감마선 영역이고 물질이 고체·액체·기체이며, 방출된 입자가 전자나 이온(대전된 원자 혹은 분자)인 경우도 포함된다(→ 계면, 전자기복사, 복사).
광전효과는 1887년 독일의 물리학자 하인리히 루돌프 헤르츠가 발견했다.
그는 자외선을 쪼임으로써 주어진 금속전극들 사이에서 방전현상이 일어날 수 있는 최저전압을 변화시킬 수 있다는 것을 관찰했다.
19세기 말엽, 음극선(희박한 기체상태에서 전기방전에 의해 생성됨)은 전기적으로 각각 음의 전하를 갖고, 전자라고 하는 불연속적인 입자들로 이루어졌다는 것이 입증되었다.
`1900년 독일의 물리학자 필리프 에드바르트 안톤 레나르트는 금속 표면에 빛을 쪼였을 때 금속에서 나오는 전하를 연구한 결과, 그 전하들이 음극선에서 관찰된 전자들과 동일한 것이라는 결론을 내렸다.
더 나아가서 금속에서 자유로워진 전자가 흘러 발생시키는 전류(빛에 의해 발생하므로 광전류라는 이름이 붙었음)는 일정한 파장의 빛을 쪼일 경우 빛의 세기에 비례한다는 것도 발견했다.
1902년에는 광전효과로 발생하는 전자의 최대 운동에너지는 빛의 세기에는 무관하고 진동수에 의존한다는 사실이 입증되었다.
광전효과로 방출되는 전자의 수는 쪼인 빛의 세기에 비례하고 빛의 진동수나 파장은 전자의 최대 운동에너지를 결정한다는 관찰은 고전물리학으로 설명할 수 없었던 빛과 물질 사이의 상호작용이 있음을 시사했다.
이러한 사실에 대한 설명을 탐구하는 과정에서 1905년 알베르트 아인슈타인은 그동안 파동으로만 생각했던 빛이 에너지 양자라는 불연속적인 입자들(지금은 광자라고 부름)로 구성되어 있다는 기본이론을 제시했다.
아인슈타인은 광전효과를 설명하면서 광자는 물질을 투과할 수 있으며, 이 과정에서 원자와 충돌할 것이라고 가정했다.
모든 원자는 전자를 가지고 있어 충돌할 때 광자의 에너지에 의해 원자로부터 전자가 빠른 속도로 방출되며, 이 전자는 물질 내부의 원자 사이를 움직여 원자와 충돌할 때마다 자신의 운동에너지를 잃게 된다.
또 전자가 물질의 표면에 도달하면, 전자는 표면 원자들의 인력을 극복하고 벗어나는 과정에서 더 많은 운동에너지를 잃는다.
이렇게 손실된 운동에너지를 일함수(work function)라고 하며, 오메가(ω)로 표시한다.
아인슈타인의 설명에 따르면, 개개의 광자는 플랑크 상수(h)와 빛의 진동수(그리스 문자로 ν)와의 곱에 해당하는 에너지로 이루어져 있다.
따라서 그는 광전효과에 관한 이론에서 물질에서 방출되는 전자가 갖는 최대 운동에너지는 쪼인 빛의 진동수와 플랑크 상수의 곱에서 일함수를 뺀 값과 같다고 가정했다.
결과적으로 광전효과에 대한 아인슈타인의 방정식은 Εk=hν-ω로 표현된다.
여기서 Εk 전자의 최대 운동에너지이고, h는 플랑크 상수(나중에 플랑크 상수와 수치가 같다는 것이 밝혀짐), ν는 쪼인 빛의 진동수, ω는 일함수를 나타낸다(→ 전자 일함수).
방출된 전자의 운동에너지는 전기장 안에서 방출된 전자의 속도를 0으로 만드는 데 필요한 전위차(V로 표시됨)를 측정함으로써 얻을 수 있는데, 이 에너지는 전위차와 전자가 가지는 전하량(항상 상수값이며 e로 표시됨)의 곱으로 나타난다.
즉 Ek=eV이다.
아인슈타인의 관계식은 그동안 많은 과학자들에 의해 검토되어 원리적으로는 옳지만 현상의 기술에는 완전하지 못한 것으로 밝혀졌다. 특히 그 관계식은 방출된 전자의 에너지가 물질의 온도에 영향을 받는다는 사실을 설명하지 못했다.
그후 1931년 영국의 수학자 랄프 하워드 파울러는 이 결점을 보완하여 새로운 관계식을 만들었다.
그는 일함수보다 큰 에너지를 갖는 전자들은 모두 방출된다는 가정 아래 광전류와 온도의 관계를 입증했다.
즉 광전류는 온도의 제곱과 입사되는 광자가 가진 에너지함수에 비례하는데, 방정식은 I=aAT2φ (χ)로 표현된다.
여기서 Ι는 광전류, α와 A는 상수, φ(χ)는 수치가 도표화된 지수급수이고, 차원이 없는 값인 χ는 방출된 전자의 운동에너지를 온도와 운동이론의 볼츠만 상수의 곱으로 나눈 값이고, χ=(hν-ω)/kT로 표현된다.
여기서 x는 지수급수의 변수, h는 플랑크 상수, ν는 쪼인 빛의 진동수, ω는 물질의 일함수, k는 볼츠만 상수, 그리고 T는 온도이다.
처음 광방출에 대한 연구 중 대부분은 전기전도율이 좋은 고체금속의 방출특성에 집중되었다.
그러나 점차 부피와 표면불순물 효과를 인식하면서 부도체인 절연체와 정해진 조건에서만 전기가 전도되는 반도체의 광전자 방출에도 관심을 가지기 시작했다.
절연체와 반도체에서 전자의 에너지 분포는 금속의 경우와 다르다. 즉 일함수가 같더라도 입사광자가 가지는 에너지와 광전자산출량(입사되는 각각의 복사양자에서 방출되는 전자의 수)의 비는 물질에 따라 다를 수 있다(→ 양자 수득률).
반도체에서의 광전효과는 양자역학으로만 설명된다.
고체는 조그마한 결정들로 이루어졌다고 볼 수 있다.
또 이 결정들은 격자구조라고 하는 3차원의 규칙적인 원자배열을 갖고 있다. 원자에 구속되어 있거나 혹은 자유상태로 있거나 관계없이 격자 안의 모든 전자들은 에너지상태라는 제한된 에너지를 갖는다.
여기서 에너지상태들은 결정의 격자구조에 영향을 받는다. 전자들은 열이나 전자기 에너지를 흡수해서 더 높은 에너지 상태로 옮겨갈 수 있다. 양자역학 법칙에 따르면 불연속적이며 특정한 에너지 상태만이 존재하며, 이들은 에너지대(energy band)에 모여 있다.
이 에너지대 사이에는 금지대(forbidden band)라는 영역이 존재한다.
결정이 절대온도 0℃의 상태에 있을 때 전자가 채워지는 가장 높은 에너지대를 가전자대(valence band)라고 한다.
만약 이 가전자대가 채워지지 않은 상태를 포함하고 있다면 이 영역을 전도대(conduction band)라고 하며, 이때 결정은 금속이 된다.
만약 모든 상태들이 채워져 있다면 이 결정은 전자들이 가전자대로부터 다음의 채워지지 않은 영역으로 옮겨가 전도대로 될 수 있는가의 여부에 따라 절연체 혹은 반도체가 된다.
반도체의 경우 빛의 형태로 에너지를 주어 원자가전자를 전도대로 올려놓을 수 있다.
또 금지대의 간격에서 에너지 준위(準位)를 갖는 불순물 원자라고 하는 원자들이 반도체에 전자를 공급할 수 있다. 절연체의 경우 금지대의 간격이 너무 커서 전자들이 쉽게 옮겨갈 수 없다(→ 결정격자, 전이).
광전도도의 원리와 특성
많은 물질들은 빛을 쪼였을 때 전기전도도 면에서 주목할 만한 변화를 보인다. 여기에는 상반된 몇 가지 반작용의 예가 있지만, 보통 전도도는 증가한다. 금속과 같이 전도도가 높은 물질에서는 전도도의 변화를 무시할 수 있지만 반도체의 경우에서는 가장 중요한 현상이 된다(→ 비저항).
반도체 내에는 전도대 안에서 에너지 준위를 채우고 있는 약간의 자유전자와 원자의 자연진동으로 전도대로 옮겨진 자유전자들로 인해, 가전자대 안에 남겨진 양전하를 띤 몇 개의 양공(陽孔 hole)이 있다.
물질에 빛을 쪼이는 동안 자유전하운반자(전자, 양공)가 많이 생성되어 전도도가 증가되는데, 광자흡수로 생성된 운반자들이 금속 내부에서 더이상 움직일 수 없을 때까지 자유전하운반자들은 계속 생성된다. 이들의 전기적 과정은 물질의 띠구조(band structure)와 결함 그리고 다른 여러 요인에 따라 다양하다.
감광도(광자 1개 흡수당 전도율의 변화)를 결정할 때 가장 중요한 요인 중 하나는 자유운반자의 수명이다. 즉 음의 전하를 띤 전자와 양의 전하를 띤 양공들끼리의 재결합 혹은 중화로 인해 그 수명은 유한하며, 이로 인해 전도과정에 기여할 수 있는 전자의 수는 준다. 수명은 10-2~10-12초 사이인데 물질에 따라 다르며, 한 물질 내에서도 결함이나 불순물의 정도에 따라 다르다.
감광도를 결정하는 또 하나의 요인으로 광전도체의 빛 흡수 특성이 있다.
광자가 가진 에너지가 고체의 금지대 에너지 간격보다 클 때 각각의 광자는 1개의 자유전자와 1개의 자유양공으로 된 자유쌍을 생성한다. 광자의 에너지가 금지대의 에너지 간격보다 훨씬 크다면(예를 들어 X선의 광자가 가진 에너지처럼), 광자를 1개 흡수해서 여러 개의 자유쌍을 만들 수 있다.
광기전효과의 원리와 특성
광기전효과(photovoltaic effect)는 물질이 복사선을 흡수하여 기전력이 생성될 때 일어난다. 즉 빛을 다른 두 물질의 경계면에 쪼였을 경우 전류가 경계면을 지나 흐른다.
주된 효과로는 같은 수의 양전하와 음전하를 생성시키는 광이온화가 있다. 광이온화가 일어나면 1개 혹은 2개의 전하는 전하분리가 일어날 수 있는 영역으로 옮겨갈 수 있고, 이러한 전하분리는 보통 고체물질의 두 층 사이에 있는 퍼텐셜 장벽(potential barrier)에서 일어난다.
광기전효과를 크게 하기 위해서는 장벽에서 퍼텐셜변화가 커야 하고 전하운반자가 이동할 거리가 짧아야 한다. 이 효과는 전도도가 갑자기 변하는 것을 포함하여 물질의 어떤 특성이 갑자기 변하는 것을 의미한다. 광기전효과의 반응시간은 광전자방출처럼 순간적이지는 않지만 비교적 짧다. 광기전효과의 중요한 특성은 복사에너지를 전류로 바꾸는 장치로서 비교적 높은 효율을 갖는다는 점이다(→ 태양 에너지).
여러 가지 광전자방출현상
광전자방출현상은 X선과 감마선 같은 높은 에너지영역에서 잘 알려져 있는데, 이런 투과력이 강한 복사는 내부 원자껍질에서 광전자를 방출시킬 수 있기 때문이다.
광전과정으로 전자가 떨어져나가 원자의 내부 껍질에 빈자리가 생기면 이 빈자리는 그보다 약하게 속박된 상태에 있는 전자로 채워지고, 이 과정에서 남은 에너지는 다시 또다른 그보다 약하게 속박된 상태에 있는 오제 전자(Auger electron)라고 하는 2차 전자를 동시에 방출시킨다. 이런 현상을 오제 효과라고 하는데, 높은 에너지에서 주로 관찰된다. 여러 종류의 오제 변환이 일어나면 주어진 내부에 빈자리가 생긴다.
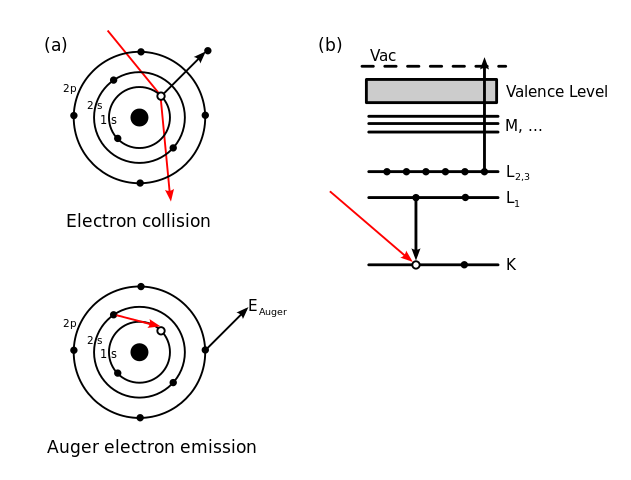
오제 전자(Auger electron)
오제 프로세스의 두가지 뷰
ⓒ A. Carlson/wikipedia | Public Domain
이러한 특성 때문에 고분해능 분광학의 발달과 낮은 에너지의 전자에 대한 연구가 함께 진척되면서, 오제 효과는 포획 또는 내부변환과 같은 여러 핵과정의 연구에 중요한 역할을 하게 되었다. 또 오제 전자가 가진 에너지와 세기를 알면 원자와 분자에서 전이확률에 관한 정보를 알 수 있으며, 역으로 에너지 값을 정확히 알고 있는 오제 분광선은 전환전자의 에너지 측정에 사용될 수 있다(→ 감마선).
그외 중요한 광전자방출과정으로 콤프턴 효과가 있는데, 이것은 광자와 전자가 충돌한 후 이들이 진행하는 방향과 관련이 있다. 고에너지를 가진 광자가 초기에 정지해 있는 전자와 충돌하면 광자는 약간의 에너지와 운동량을 전자에게 주어 광자와 전자는 각기 다른 경로로 튀어나간다. 에너지와 운동량보존법칙에 따르면 전자의 운동에너지는 입사광자의 에너지에 의존하는 반면, 입사광자의 파장에 있어 콤프턴 편이(Compton shift)는 광자의 에너지와 관계가 없다.
충돌 전후에 파장의 증가를 나타내는 입사광자와 산란된 광자 사이의 파장에 대한 콤프턴 편이는 다음 두 항의 곱으로 나타낸다. 즉 첫째 항은 플랑크 상수와 전자의 정지질량(상대론에 따르면, 물체는 관측자에 대해 상대적으로 정지해 있을 때 최소 질량을 갖는다)에 광속을 곱한 값의 비율이며, 둘째 항은 산란된 광자와 입사광자의 경로가 이루는 각의 코사인값과 1과의 차(差)이다. 이를 식으로 표현하면 Δλ=(h/moc) (1-cosθ)인데 여기서 Δλ는 파장의 편이이고 h는 플랑크 상수, mo는 전자의 정지질량, c는 광속, θ는 광자의 산란각을 나타낸다.
광자의 산란각이 90°일 때의 (h/moc)항을 모든 전자에 대해 콤프턴 파장이라 하며, 이것은 2.4262×10-10㎝ 값을 갖는, 길이의 기본적인 원자단위이다. 원자, 전자 그리고 핵들은 여러 가능한 방법으로 전자기복사와 상호작용한다. 낮은 에너지에서는 광전효과가, 아주 높은 에너지에서는 쌍생성이 우세한 반면, 복사가 거의 콤프턴 산란에만 의존하는 넓은 에너지 영역이 존재한다.
응용
극도로 짧은 반응시간 동안 빛의 세기에 비례하는 반응을 이용한 광전자방출의 여러 가지 기술적인 변형장치가 있다. 광전자방출장치(광다이오드)는 적합한 증폭장치와 연결할 수 있으며, 이럴 경우 단 1개의 광자도 증폭시켜 감지할 수 있다.
가장 잘 알려진 증폭장치로는 광전자증배관이 있는데, 이것은 같은 용기에 2차 방출기를 적절히 조합하여 만든다. 광다이오드와 광전자증배관은 산업생산과 제조과정의 조절, 빛의 세기 측정, 섬광계수기, 팩시밀리 전송, 분광분석, 그외 여러 분야에서 사용범위가 점점 늘고 있다(→ 다이오드).
광전자방출기의 표면에 비치는 모든 빛을 광다이오드와 광전자증배관으로 모으면 받아들인 빛의 총량을 알 수 있다. 영상변환관, 영상증폭관, 텔레비전 촬상관, 영상기록관 등은 점 방식으로 방출되는 광음극을 이용한 것이다. 앞의 두 예인 영상변환관과 영상증폭관은 광음극에 광상을 입사시켜 빛으로 된 영상을 '전자영상'으로 바꾸는 데 사용된다.
광전자방출기에서 방출된 전자들이 전자광학장치(electron-optical device)로 형광면(fluorescent screen)에 초점을 맞추면, 전자는 광상으로 다시 바뀐다. 이 과정은 한 단계나 여러 단계를 거쳐 이루어지는데, 각 단계마다 영상은 증폭된다. 텔레비전 촬상관의 가장 보편적인 형태 중에서 영상변환관은 첫 단계로 광음극으로부터 나오는 전자영상을 절연물질로 옮긴다. 이때 2차 전자방출을 통해 일련의 양전하 무리들이 발생한다. 또다른 전자선속이 표적에 주사되면 물질 표면에 있는 전하의 영향을 받아 그곳의 정보를 2차 전자증배관에 전달한다. 이때 증폭된 신호는 외부 회로로 나간다(→ 전자관).
광전도체 역시 폭넓게 사용되는데, 주로 박막 장치의 형태로 기록관(storage tube), 텔레비전 픽업관(소리나 빛을 전기로 바꾸는 장치), 디스플레이 장치(display device), 복사조절가변저항기, 전자 스위치, 영상증폭관, X선 증폭관, 전자사진기 등에 사용된다.
복사선검출기로 쓰이는 광전도체는 광전자방출기로 얻을 수 있는 것에 비해 더 낮은 입사광자 에너지까지 분광범위를 확장시켜준다. 지금까지는 인듐-안티몬 검출기와 같은 적외선검출기에 대해 설명하였는데, 이것들은 0.15eV(electron volt)에서 최저 에너지 한계를 가진다. 적외선 검출에 사용되는 특수한 검출기들은 0.030∼0.040eV에 해당하는 낮은 에너지 한계를 갖고 상품화되어 있다. 규소검출기는 X선과 감마선검출기 그리고 분광분석 등에 폭넓게 쓰인다(→ 방사선 측정).
광기전 장치들은 주로 분광의 가시광선 영역에서 효율성이 높기 때문에 사진기의 조도계 또는 그와 비슷한 장치들에서 사용되었고, 에너지 변환장치로서 그 우수성을 인정받았다. 지금은 태양전지가 개발되어 여러 전기장치의 작동에 필요한 전력을 공급한다.