우리는 지금까지 4-velocity와 4-momentum이라는 개념을 배웠습니다.
이들 개념은 기존의 "속도"와 "운동량"을 4차원 시공간으로 확장한 것인데요,
마찬가지로 오늘은, 전자기학의 "벡터 퍼텐셜"을 4차원 시공간으로 확장해 볼 것입니다.
거두절미하고, 결과부터 말씀드리겠습니다.
"4차원 벡터 퍼텐셜 (4-potential; 포 퍼텐셜)" A는, 아래와 같이 정의됩니다.
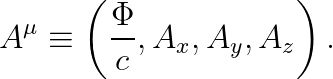
즉, 4-potential A의 0번째 성분은 "전기퍼텐셜 Φ"이며, 나머지 성분은 벡터 퍼텐셜의 형태로 주어집니다.
문제 민코프스키 메트릭에 대해, 아래의 값을 구하여라.
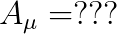
답 우선, 0번째 성분부터 구해 볼까요?
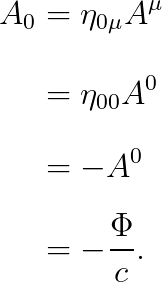
같은 방법으로, 아래의 결과를 얻습니다.
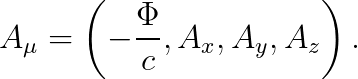
이를 사용하여 라그랑지안을 구해 보겠습니다.
기존의 고전역학 라그랑지안은, 여러 가지 물리량을 조합해서 만들어 내었지만,
상대론적 라그랑지안은 간단하게 "길이"로 주어졌습니다 ("12강" 참조):
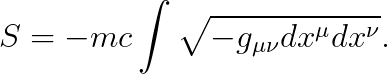
전자기장이 포함된 경우에도, 라그랑지안이 상당히 간단하게 주어지는데요,
아래와 같이, 4-potential의 선적분을 고려해 봅시다.
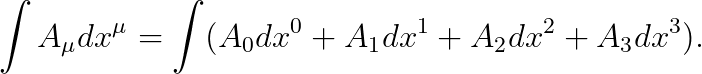
위의 선적분에, 전하량 q를 곱하면 액션이 주어집니다:
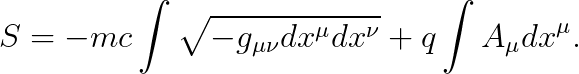
위의 액션이 맞는지 확인하기 위해, 아래의 값을 계산해 봅시다.
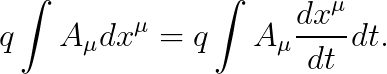
이때, 다음이 성립합니다.
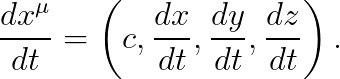
따라서,
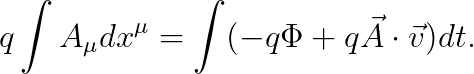
이는 전자기학 "24강"에서 배웠던 라그랑지안과 일치하는 결과입니다.
이것으로 4차원 벡터 퍼텐셜에 대해 배워 보았는데요,
그렇다면 전기장과 자기장은 4차원 시공간에서 어떻게 나타날까요?
우선, 전자기학 시간에 배웠던 바에 의하면, 자기장은 벡터 퍼텐셜의 "컬 (curl)"로써 주어집니다:
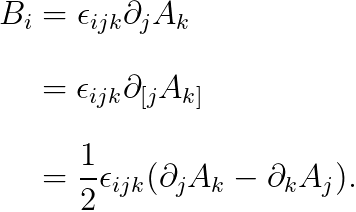
마찬가지로, 4차원 벡터 퍼텐셜에 "컬"을 취한 것을, 아래와 같이 정의합니다.
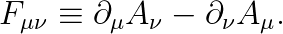
위 식에 나타난 "대문자 F"를 일컬어 "전자기장 텐서 (electromagnetic field strength tensor; 일렉트로마그네틱 필드 스트렝쓰 텐서)" 또는 "패러데이 텐서 (Faraday tensor)"라고 부릅니다.
이름이 조금 길지요? 일반적으로는 "field strength tensor" 또는 "curvature (커버쳐)"라고 부릅니다.
("Curvature"라고 부르는 이유는, 위 식의 F가 게이지 이론의 곡률을 나타내기 때문인데요, 게이지 이론에 대해서는 "상대론" 게시판에서 소개하겠습니다.)
자, 우리가 다루었던 4-potential을 다시 한 번 생각해 봅시다.
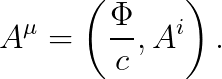
보시다시피, 일반적인 4차원 벡터를 나타낼 때에는, 0번째 성분 (A^0)과 3차원 공간에 해당하는 성분 (A^i)으로 나누어 표기합니다.
마찬가지로, field strength tensor역시, 아래와 같이 시간 성분 (0번째 성분)과 공간 성분으로 나누어 표기합니다:

이때, field strength tensor는 반대칭이므로, 다음이 성립합니다.
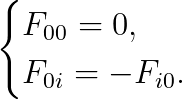
따라서, 우리는 아래의 두 성분만 구하면 됩니다.

문제 다음을 구하여라.
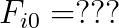
답
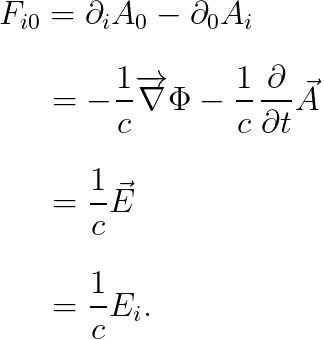
문제 다음을 구하여라.
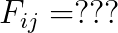
답 우선, 아래의 값을 계산해 봅시다.
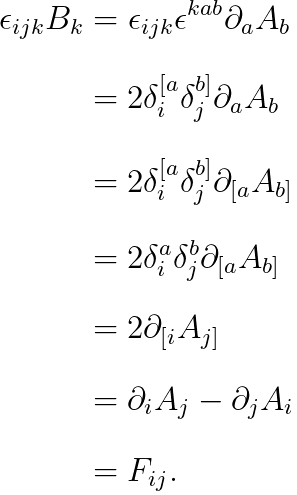
(레비-시비타 기호 관련 계산은, "11강"을 참조하세요.)
이로써, field strength tensor는 전기장과 자기장이라는 결론을 얻습니다.
이를 바탕으로 오일러-라그랑즈 방정식을 풀어 보겠습니다.
앞서 고려하였던 아래의 액션을 생각합시다.
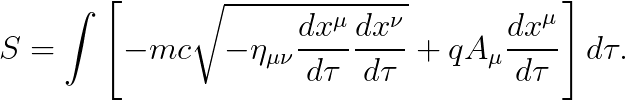
라그랑지안을 미분하면 다음을 얻습니다.
(첫 번째 항을 미분하는 것은 "12강"에서 이미 다루었으므로, 답만 쓰겠습니다.)
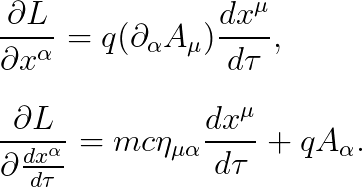
오일러-라그랑즈 방정식을 아래와 같이 기술합시다.
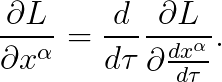
이를 풀면 다음을 얻습니다.
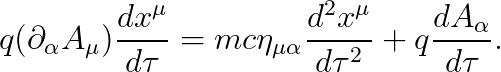
위 식에 아래의 연쇄법칙을 적용합니다.
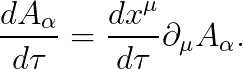
결과는 다음과 같습니다.
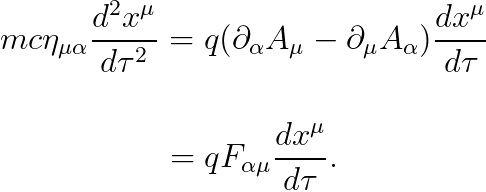
위 식에 "τ = ct"를 대입하면, 전자기학에서 배웠던 아래의 식을 유도할 수 있습니다.
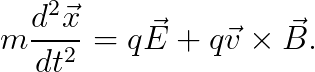
마지막으로 우리가 유도할 것은, "전기장과 자기장에 대한 액션"입니다.
우선, 고전역학적인 액션을 복습해 보겠습니다:
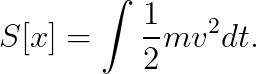
위 식은, 함수 x(t)에 대한 "범함수 (functional)"임을 고전역학 "15-16강"에서 배웠습니다.
위의 액션에 대한 "범함수의 미분"은, 다음과 같이 나타났습니다.
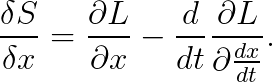
방금 다루었던 x(t)는 변수가 하나인 함수입니다.
그렇다면, 변수가 여러 개인 함수는 어떨까요?
시공간에서 변수가 4개인 함수 f(t,x,y,z)를 생각해 보겠습니다.
이러한 함수에 대해, 범함수 S[f]를 생각할 수 있으며, 범함수의 미분은 다음과 같습니다.
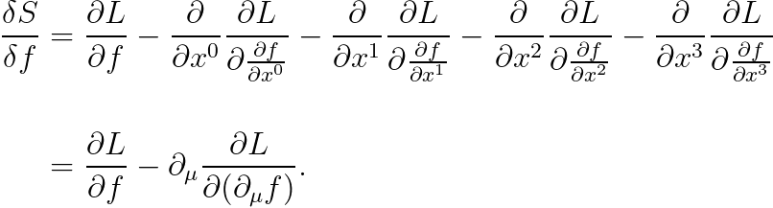
조금 복잡하지요?
(위 식을 유도하시려면, 고전역학 "15강"에서 배운 델타함수를 사용하시면 됩니다.)
그러나, 실제로 범함수를 미분하는 과정은 굉장히 간단한데요, 문제를 풀며 함께 살펴 봅시다.
문제 함수 f(t,x,y,z)에 대해, 아래와 같은 범함수를 미분하여라.
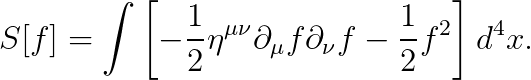
(보시다시피, f(t,x,y,z)에 대한 범함수는 4차원 적분으로 나타납니다.)
답 범함수의 미분을 축약해서 "δ (델타)"로 표기하여, 다음을 얻습니다.
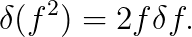
또한, 메트릭 텐서의 성분은 대칭 행렬이므로,
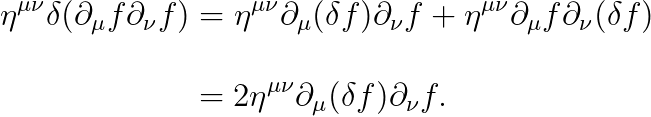
결과는 다음과 같습니다.
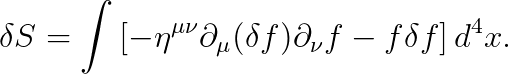
이어서, 첫 번째 항을 아래와 같이 부분적분하겠습니다.
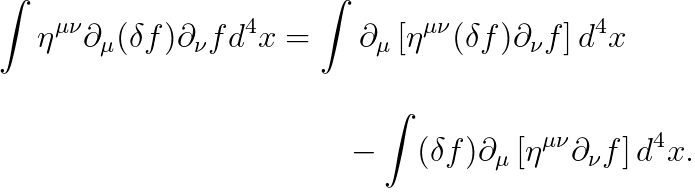
우변의 첫 번째 항에는 발산정리를 적용할 수 있는데요, 우선 우리가 알고 있던 발산정리를 기술해 보겠습니다:
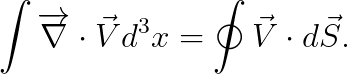
위 공식을 4차원으로 확장하면 다음을 얻습니다.
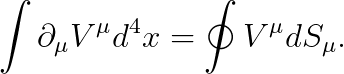
이를 바탕으로, 앞서 말씀드린 항에 발산정리를 적용할 수 있습니다:
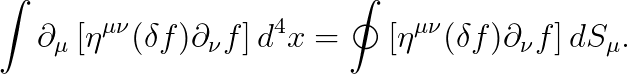
이때, 경계면의 적분 (∮)은 4차원 공간의 맨 끝부분 (한없이 먼 무한대 지점)이므로, 이 구간에서 "δf=0"입니다.
따라서, 주어진 범함수의 미분은 다음과 같이 주어집니다.
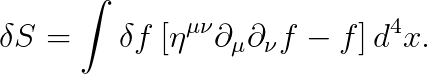
우변의 "δf"가 좌변으로 넘어가면서, 정적분이 소거됩니다:
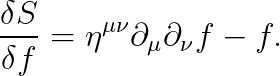
이는 오일러-라그랑즈 방정식을 푼 것과 동일한 결과이지만,
실제로 문제를 풀 때에는 위와 같이 "δ" 기호를 사용하는 것이 훨씬 편하다는 것을 강조해 두겠습니다.
자, 그러면 전자기장에 대한 논의로 넘어가 보겠습니다.
가장 먼저 해야 할 일은, 앞서 다루었던 적분을 4차원 적분으로 바꾸는 것입니다.
아래의 적분을 고려합시다.
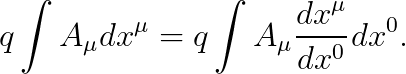
보시다시피, 4차원 적분으로 바꾸기 위해, 적분 변수를 "dx^0"로 잡았습니다.
3차원 델타함수를 사용하여 다음을 얻습니다.
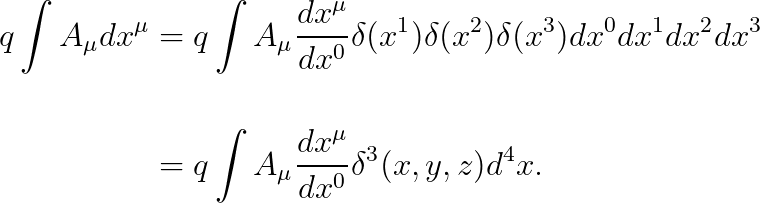
전자기학 "9강"에서 배웠듯이, 아래의 값을 "전하밀도 ρ(x,y,z)"로 나타낼 수 있습니다.
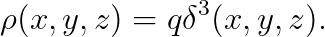
또한, 전자기학 "20강"에 의하면, "전류밀도 J"는 아래와 같이 주어집니다.
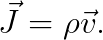
따라서, 우리는 "4차원 전류밀도 (4-current; 포 커런트)"를 다음과 같이 나타낼 것입니다.
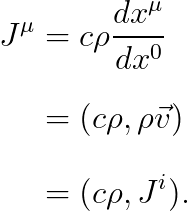
이를 바탕으로, 다음을 얻습니다.
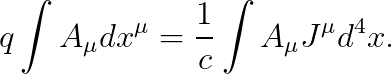
문제 아래와 같은 액션에 대해, 오일러-라그랑즈 방정식을 풀어라.
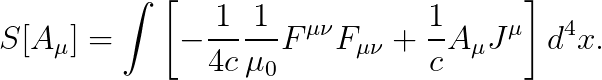
답 주어진 액션은 4-potential "A"에 대한 범함수입니다 (즉, 전류밀도 J는 상수).
두 번째 항은 쉽게 미분할 수 있으니, 첫 번째 항만 미분해 봅시다:
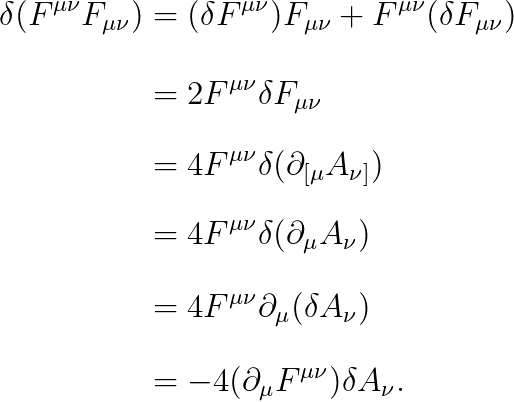
(마지막 줄에서는 부분적분하였습니다.) 따라서,
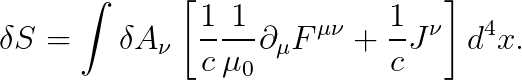
즉, 오일러-라그랑즈 방정식을 푼 결과는 다음과 같습니다.
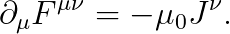
위의 수식을 풀면, 아래의 맥스웰 방정식을 얻을 수 있습니다.
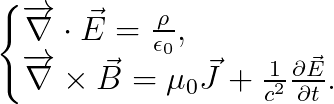
맥스웰 방정식은 모두 네 개인데, 나머지 두 개는 어디에 있을까요?
사실, 나머지 두 개는 필요가 없습니다. 왜나고요?
전자기학 "32강"에서 배운 바에 의하면, 아래의 두 개의 맥스웰 방정식을 바탕으로, 우리는 "전기퍼텐셜"과 "벡터 퍼텐셜"을 도입했습니다.

상대론에서는 이미 4-potential을 사용하고 있으므로, 위의 두 맥스웰 방정식은 필요하지 않습니다.
굳이 나머지 맥스웰 방정식을 찾고 싶으시다면, 아래의 수식을 푸시면 됩니다.
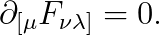
(위 식을 잘 전개해 보시면, 나머지 두 개의 맥스웰 방정식이 나옵니다.)
4-potential을 사용하면, 위 식이 trivial (트리비얼; 너무 당연해서 증명할 필요가 없음)함을 보일 수 있습니다:
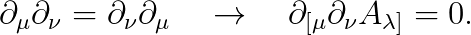
("10강"에서 배운 anti-symmetrization 공식을 잘 사용해 봅시다.)
(사족) 일부 사람들은, 민코프스키 메트릭을 아래와 같이 "부호를 바꾸어" 잡기도 합니다.
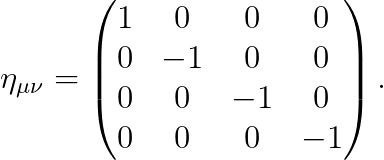
이 경우, 맥스웰 방정식 또한 아래와 같이 부호가 바뀝니다.
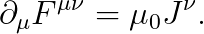
(약 절반 정도의 물리학자는 부호를 반대로 해서 씁니다. 각각의 방식이 모두 장단점이 있습니다.)