대칭 성 (symmetry)
물리학에서 대칭 성은 매우 중요한 역할을 한다.
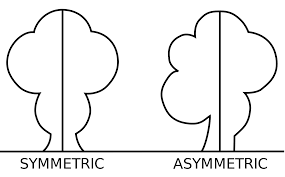
예를 들어 원의 경우 어떤 각도로 회전을 시켜도 모양은 변하지 않는다.
이 것이 대칭 성이다.
뇌터의 정리 (Noether's theorem)
어떤 물리 계의 속성에 연속적인 대칭성을 갖는다면 보존 된 값의 양은 같을 것이다.
대칭성 ↔ 보존 법칙
| 회전 대칭성 | 각 운동량 보존 | 시간 병진 대칭성 | 에너지 보존 | 공간 병진 대칭성 | 운동량 보존 | 양자 역학 대칭성 | 전하 |
왜 뇌터의 정리가 매우 중요한가 ???
보존 법칙이 대칭성에서 온 것을 증명했기 때문이다.
에미 뇌터 (Emmy Noether; 1882 ~ 1935)
에미 뇌터는 독일 바이에른 주 에를랑겐에서 태어났고 아버지 막스 뇌터는 유태인이며 대수기하학자로 에를랑겐 대학에 수학 교수로 재직하고 있었다. 에미는 영어와 불어를 가르치기 위한 자격증을 획득했지만 수학에 흥미를 느껴 1904년 에를랑겐 대학에서 수학을 공부하기 시작했고 1907년 논문 제출 후 입학 3년 만에 박사 학위를 받았다. 이 논문으로 서서히 그녀의 이름이 알려지기 시작했다. 하지만 에미는 여자라는 이유로 교수 직위는 커녕 보수조차 받지 못하고 에를랑겐 대학에서 수학을 가르쳤다.
1915년경 아인슈타인은 일반 상대성이론에 대한 마지막 손질을 보고 있었고 괴팅겐 대학의 힐베르트 (David Hilbert)와 Felix Klein은 일반 상대성 이론에서 에너지가 보존 되지 않는 문제 점에 대해 고민하고 있었다.
만약 에너지가 시공간을 휘게 하고 시공간은 에너지를 포함하고 있다면 시공간이 시공간을 포함한다는 역설이 된다.
힐베르트는 에미 뇌터가 이 문제를 해결할 수 있을 것이라 생각해 괴팅겐 대학에의 교수로 초대하자 여자라는 이유로 동료들이 반대했다. 힐베르트는 "그녀를 대학에서 가르치도록 해야 한다. 이곳은 교수단이지 탈의실이 아니다."라며 동료들을 설득했고 그 결과 힐베르트 조교로 강의할 수 있었다. 비록 그녀는 보수도 받지 못하고 대학에서 가르쳤지만 놀라울 만한 업적인 뇌터의 정리를 발표했다. 이 정리가 없었다면 아마도 일반 상대성이론은 끝내지 못했을 지도 모른다. 설상가상으로 당시 나찌즘으로 인해 유태인이었던 뇌터는 괴팅겐 대학에서 추방되었고 독일을 떠나야만 했다. 그녀는 미국으로 건너가 대학 강단에 섰지만 얼마지 않아 종양 제거 수술 후 사망했다.


연속 대칭 성 (continuous symmetry)
- 회전 대칭 성 (rotational symmetry): 어떤 물체를 회전 시켰을 때 그 물체가 변하지 않는 것을 회전 대칭 성이라고 한다. 예를 들어 수소 원자는 회전을 해도 같은 수소 원자이다.
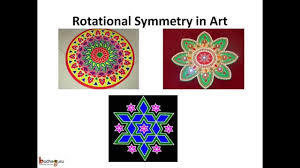
이 패턴은 회전을 시켜도 같은 패턴을 갖고 있는데 이것을 회전 대칭 성이라고 한다.
- 병진 대칭 성 (translational symmetry: 공간 병진 대칭성, 시간 병진 대칭성) - 회전이나 반사가 아닌 시간 혹은 공간의 변환에도 그 물리 계가 변하지 않는 것을 말한다. 예를 들어 어떤 에너지를 가진 입자가 공간을 달리해도 입자의 에너지는 변하지 않는다.
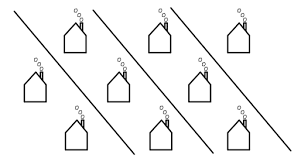
이 패턴은 좌우, 상하, 앞뒤 등 거리의 변환에도 같은 패턴을 갖고 있는데 이것을 병진 대칭 성이라고 한다.
----------------------------------------------
"어떤 미분가능한 한 물리계의 작용의 대칭성이 하나의 보존법칙에 대응된다"
이론물리의 주요 업적중의 하나인 뇌터의 정리. 물리학에서 아주 큰 업적을 남겼음에도 에미 뇌터의 이름을 아는 사람은 흔하지 않지요. 뇌터의 이전에는 계속해서 관찰되는 자연계의 어떤 알 수 없는 약속이 법칙이었습니다.
뇌터는 관찰로만 이루어진, 정확히 파악이 안되어 불안불안했던 '발견된 법칙'을 '아름다운 자연의 법칙'으로 이해할 수 있게 해주었습니다.
라그랑주 역학과 대칭성, 운동량 보존법칙
온전히 이것을 이해하기 위해서는 물리학부 2학년 수준이 필요하고, 여기서는 수식없이 간단하고 비유적으로 설명하는것을 중점으로 두도록 하겠습니다.
라그랑주 역학은 "어떤 물체들이 물리적으로 같은 물리량을 가지고 있을 때, 그것을 상관하지 않겠다"고 하는 것입니다. 물체의 운동이 일어나는 2차원 공간에서 이 생각을 풀어보도록 합시다.
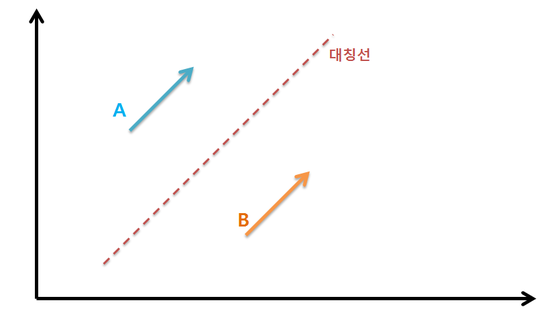
A와 B라는 두 화살표는 서로 다른 지점에서 출발하지만, 대칭선을 따라 2차원 공간을 접으면, 두 화살표는 완전히 맞물리게됩니다. 이 2차원에서는 한 점이 다른점보다 특별하지 않습니다. 심지어 기준이 되는 (0,0) 점도 어떤 의미를 가지고 특별히 정한게 아닙니다. 즉, 화살표의 '위치'는 어떤 특별함을 가지고 있지 않을 뿐더러 마음대로 바꿀수도 있지요. '위치'라는건 라그랑주 역학의 입장에서는 없어져도 상관 없는 것입니다.
그렇다면, 여기서 변하면 안되는 것이 무엇이 있을까요?
네, 화살표의 '방향'과 '크기'입니다. 이것들은 둘이 동시에 같은양으로 변하는게 아니라면, 더이상 대칭성을 가질 수 없습니다. 그리고 그 둘이 변하지 않는다면 어떤 위치에서 보더라도, 이것들은 대칭성을 가지는 같은 화살표로 생각할 수 있을 겁니다. 고등학교 과정에서 '벡터'에 대한 이야기와 다르지 않습니다.
이것이 translational symmetry이 됩니다. - 링크해주신 분은 길이 방향 이동에 대한 대칭성이라 하셨지만, 저는 병진(竝進) 대칭성이라고 부르도록하겠습니다. 개인적으로는 병진의 둘 이상이 함께 나아간다는 뜻이 설명에 더 부합할듯 합니다. -
리처드 파인만의 QED강의에 나온 대로 화살표는 물리학의 많은 부분을 설명할 수 있는 아주 유용한 도구입니다. 특별히 이 화살표가 물체의 운동을 가리킨다면, 운동량의 방향과 크기가 변하지 않는다면, 어디에서도 운동량은 변하지 않는다는 것. 이것이 뇌터의 정리에 의해 하나의 보존법칙이 등장합니다. 운동량 보존 법칙이지요.
헤밀턴 역학과 시간대칭, 에너지 보존
헤밀톤 역학은 양자역학과 깊은 관련을 가지고 있습니다. 운동량 공간에 관심을 가지고 운동을 풀어나가는데, 앞서서 공간의 대칭성에 대한 상황과는 다르게, 운동량을 변화시키는 힘들이 관심대산에 포함되어 있습니다.
운동량이 변하기 때문에, 운동량 보존을 사용할 수가 없습니다. 이곳에서는 새로운 대칭성이 필요했고, 시간이 새로운 대칭성을 보여주게 됩니다.
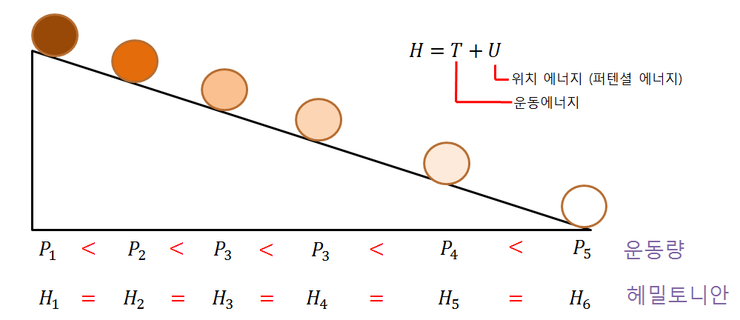
위의 상황에서 속도가 계속 증가하면서 운동량은 시간에 따라 점점 커지지만, 운동에너지와 위치에너지의 합인 헤밀토니안은 변하지 않는것을 볼 수 있습니다. 그러니까 헤밀토니안은 시간에 대해 대칭성을 가지고 있는 것이고, 이 시간 대칭성을 가지고 있는 헤밀토니안은 에너지의 합입니다.
즉, 에너지의 합은 시간에 대해 대칭성을 가지고 있고, 이것은 에너지보존법칙이 등장할 수 있게 합니다.