우리는 앞선 포스팅을 통해 상대성이론과 양자역학의 탄생 과정을 살펴보았습니다.
그리고 이 두 이론은 현대물리학을 지탱하는 두 축으로써 우리의 세상이 서로 특정 조건을 넘어서면 더는 상식이 통하지 않는다는 놀라운 사실 또한 보여주었죠.
상대성이론은 빛의 속도와 가까워질 때 길이 수축과 질량의 증가, 그리고 시간 지연효과를, 양자역학은 우리 눈에 보이지 않을 만큼 작은 미시세계에선 입자들이 파동의 성질 또한 갖는다는 것과 연속적이지 않은 움직임을 갖는다는 것을 보여주었습니다.
이렇듯 두 이론은 서로 다른 세상을 설명하는 듯하지만 넓은 의미에선 같은 우주를 설명하고자 하는 공통된 목표를 가지고 있었기 때문에 서로를 가로막는 벽은 허물어져야만 했죠.
아인슈타인의 상대성이론과 뉴턴의 고전역학의 차이점은 상대성이론이 '너와 나의 공간과 시간은 다르게 흐른다.
즉, 각자의 공간과 시간을 서로 같은 프레임에 놓고 해석한다는 것에서부터 시작합니다.
그리고 이러한 해석은 빛의 속도는 고정되어 있다는 광속불변의 원리와 E는 m 곱하기 c의 제곱이다는 그 유명한 식을 탄생케 했죠.
이 식을 말로 풀어서 설명하자면,
'물질은 질량에 빛의 속도를 두 번 곱한 만큼의 에너지를 지닌다'가 됩니다.
여기서 빛의 속도는 불변이기에 에너지와 질량 둘 중 하나의 변화는 서로의 변화를 유도하게 되죠.
이 말인즉, 에너지와 질량은 같은 것이기에 결과적으로 질량을 지닌 물질은 빛의 속도에 도달하기 위해 공급받은 무한한 에너지를 무한한 질량으로 변환하게 된다는 것입니다.
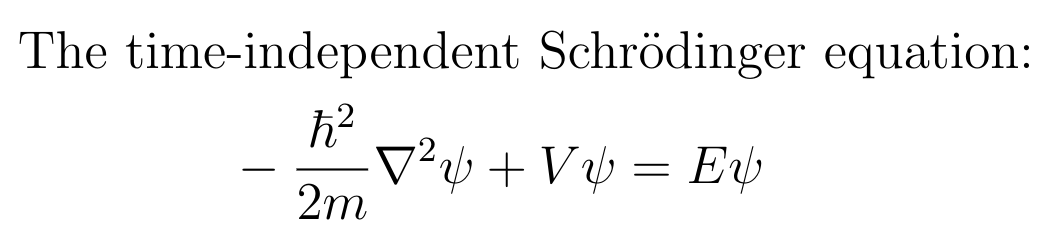
반면 양자역학에서 전자의 움직임을 기술하는 슈뢰딩거 방정식은 관찰자의 기준에서의 시간만을 따지기 때문에 각자의 공간에서 하나의 시간만이 흐르게 됩니다.
공간과 시간을 같은 프레임에 놓고 보지 않은 것이죠. 이러한 해석은 그 방정식 안에서 전자가 빛의 속도와 가까워질 때
상대성이론에서 요구하는 시공간의 특성을 담지 못하게 합니다.
암묵적으로 정보가 빛의 속도보다 빠르게 전달될 수 있다고 표현하고 있는 것입니다.
즉, 슈뢰딩거의 방정식은 광속불변의 법칙과 에너지-질량 등가원리를 담고 있지 않기 때문에 비상대론적인 것이죠.
참고로 우리가 일상에서 경험하는 전류, 즉, 전자의 흐름은 우리에겐 빛과 같이 빠르게 느껴지지만 사실은 빛의 속도 대비 현저히 느리게 흐릅니다.
이것을 우리는 하늘에서 내리치는 번개를 통해서도 확인해볼 수 있죠. 만약 우리가 슬로우모션 비디오로 번개를 촬영하게 된다면 하늘에서 땅으로 내리치는 모습을 순차적으로 확인해볼 수 있지만, 하늘을 향해 쏘아진 레이저 빛은 영화 스타워즈의 그것과는 달리 그저 한 프레임 차이로 번쩍일 것입니다.
이렇듯 슈뢰딩거의 방정식은 전자의 이동 속도가 빛의 속도 대비 현저히 느린 경우에만 만족하는 방정식이기에 빛의 속도와 가까운 경우에는 제대로 기술될 수 없습니다.
하지만 원자 속 전자들은 종종 빛의 속도에 가깝게 움직이기도 하죠. 그래서 물리학자들은 모든 상황에서의 전자의 움직임을 완벽히 설명할 수 있기를 원했습니다.
즉, 슈뢰딩거의 방정식에 아인슈타인의 특수상대성이론을 적용하기를 원했던 것입니다.
그리고 이를 1928년 영국의 물리학자 폴 디랙이 해내게 됩니다.
디랙의 방정식은 전자의 움직임을 나타내는 파동함수와 물질의 양자적 성질을 결정하는 플랑크상수, 그리고 상대성이론에서 다루는 빛의 속도를 모두 담고 있습니다.
그래서 디랙의 방정식은 모든 속도에서의 전자의 움직임을 완벽히 예측하게 하죠.
디랙은 이 방정식을 만들곤 그 단조로움의 수학적 아름다움에 흡족했지만, 여기엔 오류 같아 보이는 문제가 한가지 있었습니다. 우리는 상대성이론을 통해 질량과 에너지는 사실상 같다는 것을 잘 알고 있습니다.
그래서 물질은 정지해있어도 그 물질의 질량에 빛의 속도를 두 번 곱한 것만큼의 에너지를 지닌 것이 되죠.
그렇다면 슈뢰딩거 방정식을 상대론적으로 해석했다는 디랙 방정식도 분명 그 원리를 따랐을 것입니다.
그런데 막상 디랙의 방정식을 풀어보면 전자가 갖는 정지에너지는 +,-로 두 가지의 값을 가지게 됩니다.
이것은 전자가 음의 에너지도 지닐 수 있다는 것을 뜻하는 것이죠.
잠깐!
음의 에너지?
우리는 양자역학에서 보어의 원자모형을 통해 원자 속 전자는 가장 낮은 에너지 레벨부터 차곡차곡 위치할 수 있다는 것을 알고 있습니다. 이 말인즉, 높은 에너지 레벨에 위치하는 전자는 더 낮은 에너지 레벨이 비어있게 된다면 양 레벨 간의 에너지 차이만큼의 전자기파를 방출하며 내려앉아 안정되려 한다는 것입니다.
그리고 이때 전자가 존재할 수 있는 가장 낮은 에너지 레벨은 0보다는 크기 때문에 전자가 우리의 눈에서 사라지지 않고 계속 존재할 수 있는 것입니다.
하지만 디랙 방정식이 나타내는 것처럼 음의 에너지가 존재하게 된다면 0 밑으로도 무한한 음의 에너지 레벨이 존재한다는 것이 됩니다.
그렇다면 전자는 안정되기 위해 무한히 비어있는 더 낮은 에너지 레벨로 내려앉으려 할 것이고 그 과정에서 역시 무한한 에너지의 전자기파를 방출하게 되겠죠. 이것은 우리 우주의 에너지는 한정되어 있다는 물리학의 근간인 에너지보존법칙을 위배할 뿐 아니라 우리의 우주가 지금과 같은 형태를 띨 수 없다는 것을 의미하는 것입니다.
다른 물리학자 같으면 이러한 결과를 갖는 방정식에 분명 오류가 있을 것으로 생각하고 포기하려 했겠지만 디랙은 그 안에서 문제를 풀고자 하였습니다.
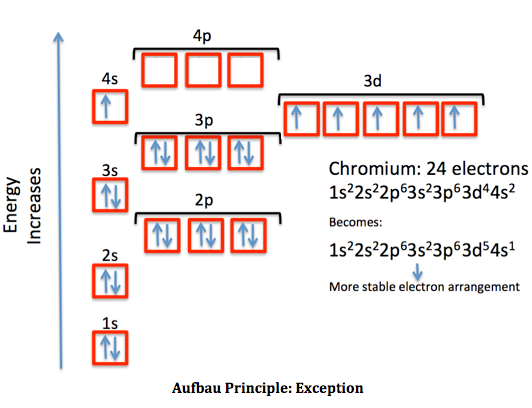
그리고 그 답을 파울리의 배타원리에서 찾게 됩니다.
디랙이 이 방정식을 만들기 4년전인 1924년, 오스트리아의 물리학자 볼프강 파울리는 원자의 구조를 설명하기 위해 배타원리를 발표하였습니다.
이 배타원리를 간단히 설명하자면, 원자 속 전자는 공간적으로 한 양자 상태에 한 개의 전자만이 들어갈 수 있다는 것입니다.
이를 우리가 이해하기 쉽게 더 풀어서 설명하자면, 질량이 없는 빛은 한 공간에 아무리 중첩되게 쏘아도 문제 될 것이 없지만, 물질인 사람의 경우 한 공간 안에 여러 사람이 중첩되게 서 있을 수 없다는 것과 같은 것이죠.
디랙은 이 배타원리를 응용해 자신의 방정식에서 발견되었던 음의 에너지가 이미 전자들로 가득 차 있을 것이라는 생각을 하였습니다.
그래서 앞의 원자핵 주변의 전자는 더는 음의 에너지 레벨로 내려갈 수 없고 양의 에너지인 물질세계에 남아있게 된다는 것입니다.
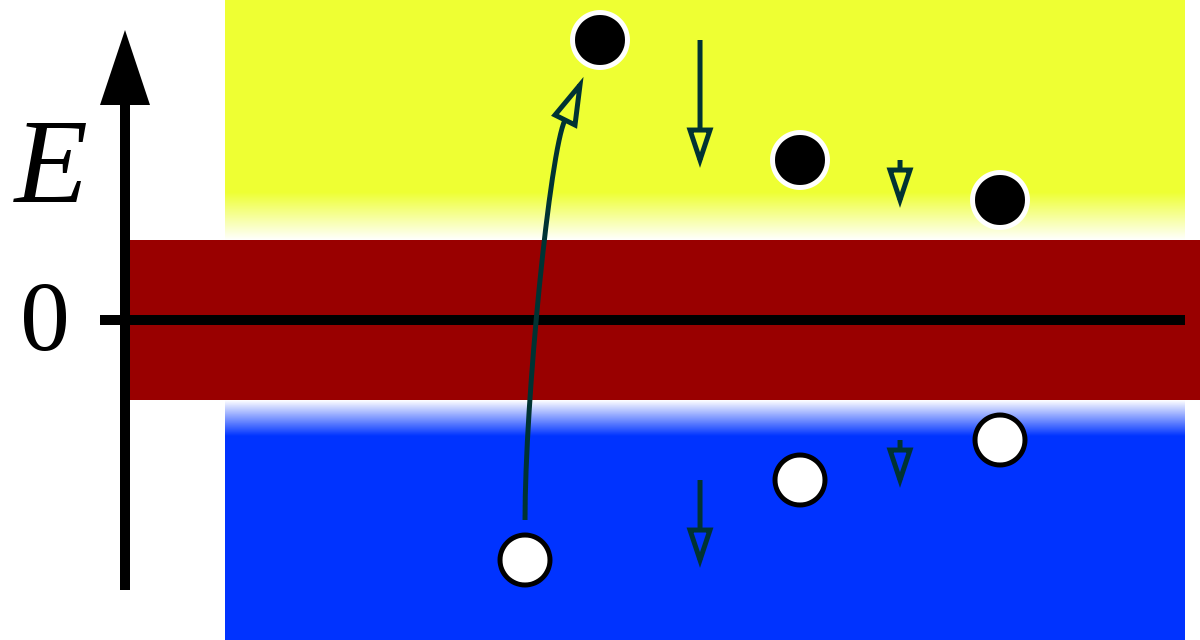
이렇게 전자들로 빼곡하게 차 있는 이 음의 에너지 영역을 우리는 훗날 디랙의 바다라고 부르게 됩니다.
이 논리에 의하면 디랙의 바다는 우리가 물리적으로 관측할 순 없지만 전 우주에 걸쳐 펼쳐져 있는 것이 되겠죠.
그런데 디랙은 여기서 의문점 한 가지를 가지게 됩니다. 자신의 방정식에서 전자가 음의 에너지로 떨어지는 것을 이미 전자들로 가득 찬 디랙의 바다를 통해 막을 수 있다면, 반대로 디랙의 바다에 있는 전자를 양의 에너지 쪽으로도 끄집어낼 수 있지 않을까?
특정 에너지의 전자기파를 쏘면 되지 않을까?
그리고 이러한 의문점은 디랙에게 또 다른 놀라운 사실을 발견해내게 해줍니다. 이것을 우리도 그의 방정식을 통해 확인해볼 수 있죠.
우리는 일상에서 어항 속 붕어가 뱉는 공기방울을 입자 처럼 관측하게 됩니다.
하지만 이 공기방울은 엄연히 물의 부재에 의해 생긴 빈공간 일뿐이죠. 즉, 우리는 물의 빈자리를 입자처럼 관측하게 되는 것입니다. 이렇듯 진공의 우주에 특정 에너지 이상의 전자기파를 쏘게 된다면 그 자리엔 두 개의 입자가 생성 된다는 것을 유추해볼 수 있습니다.
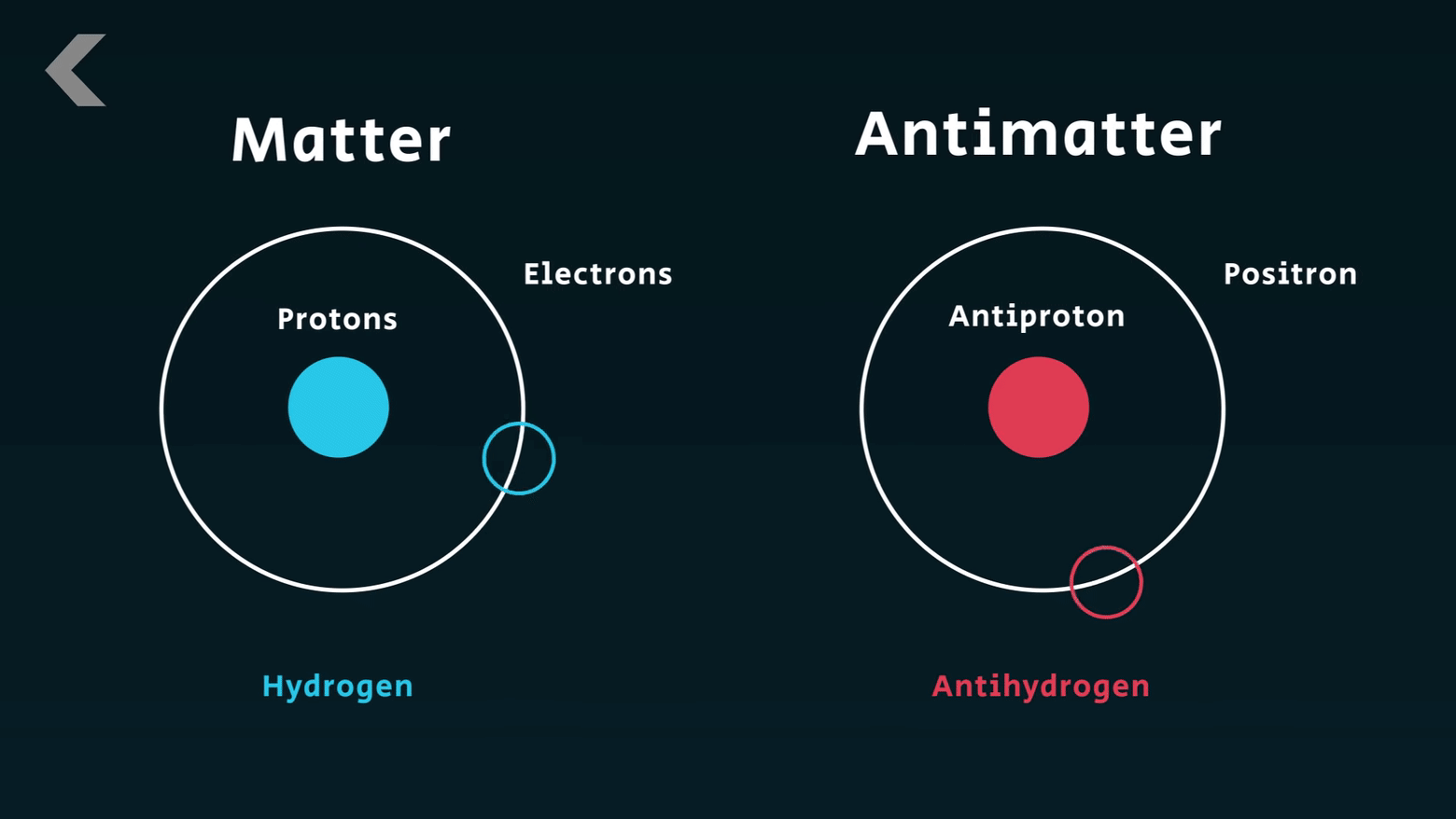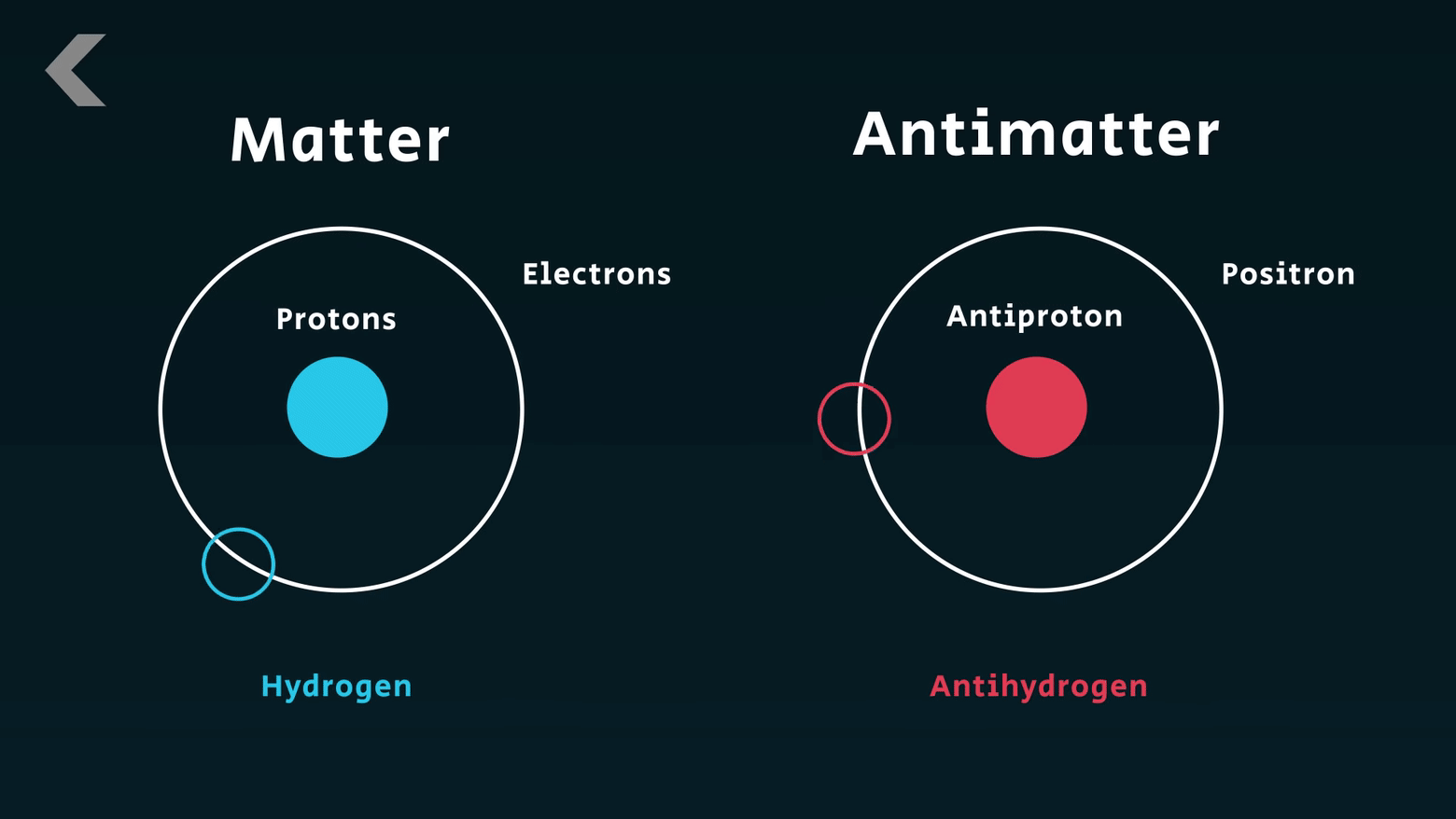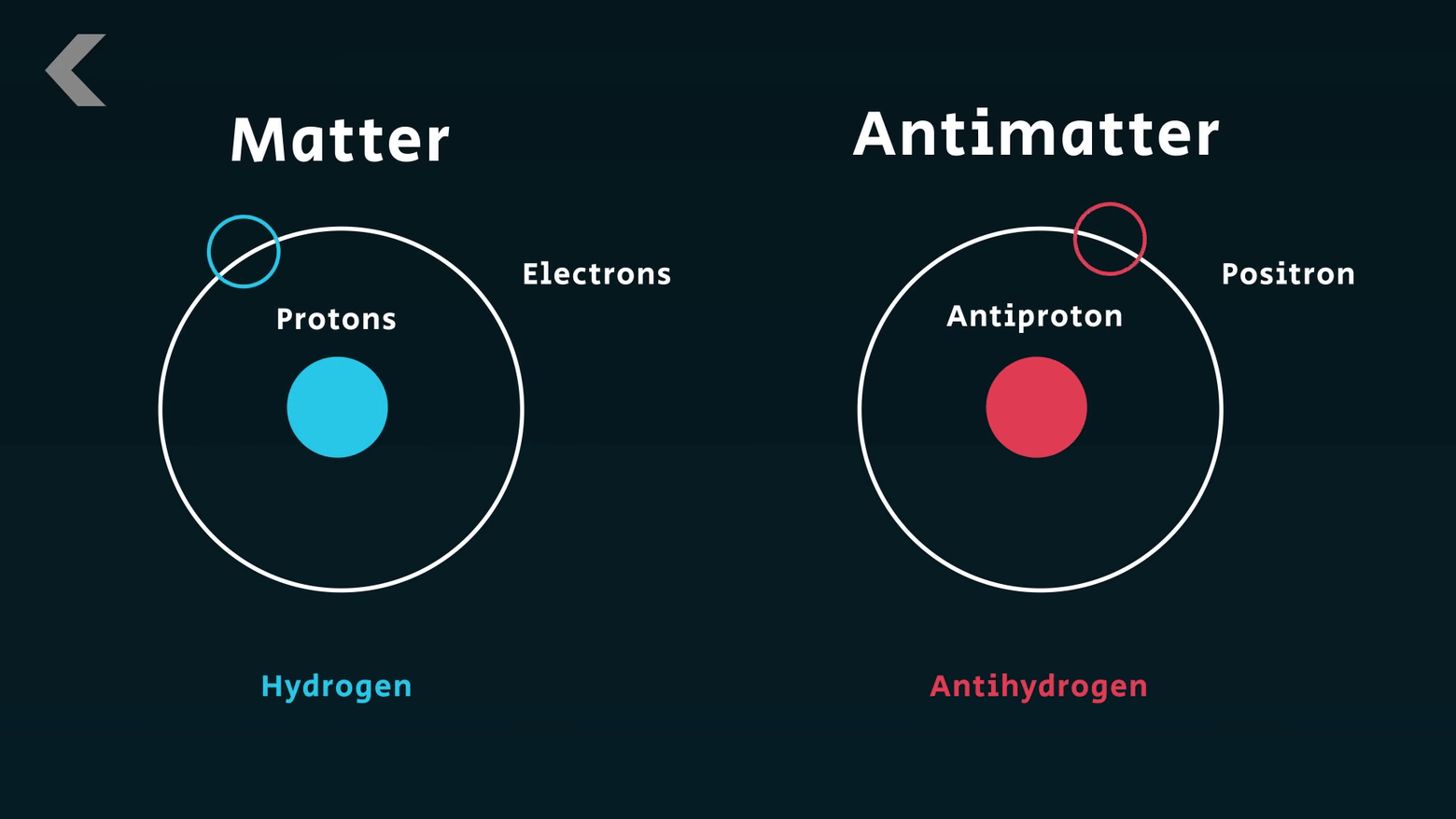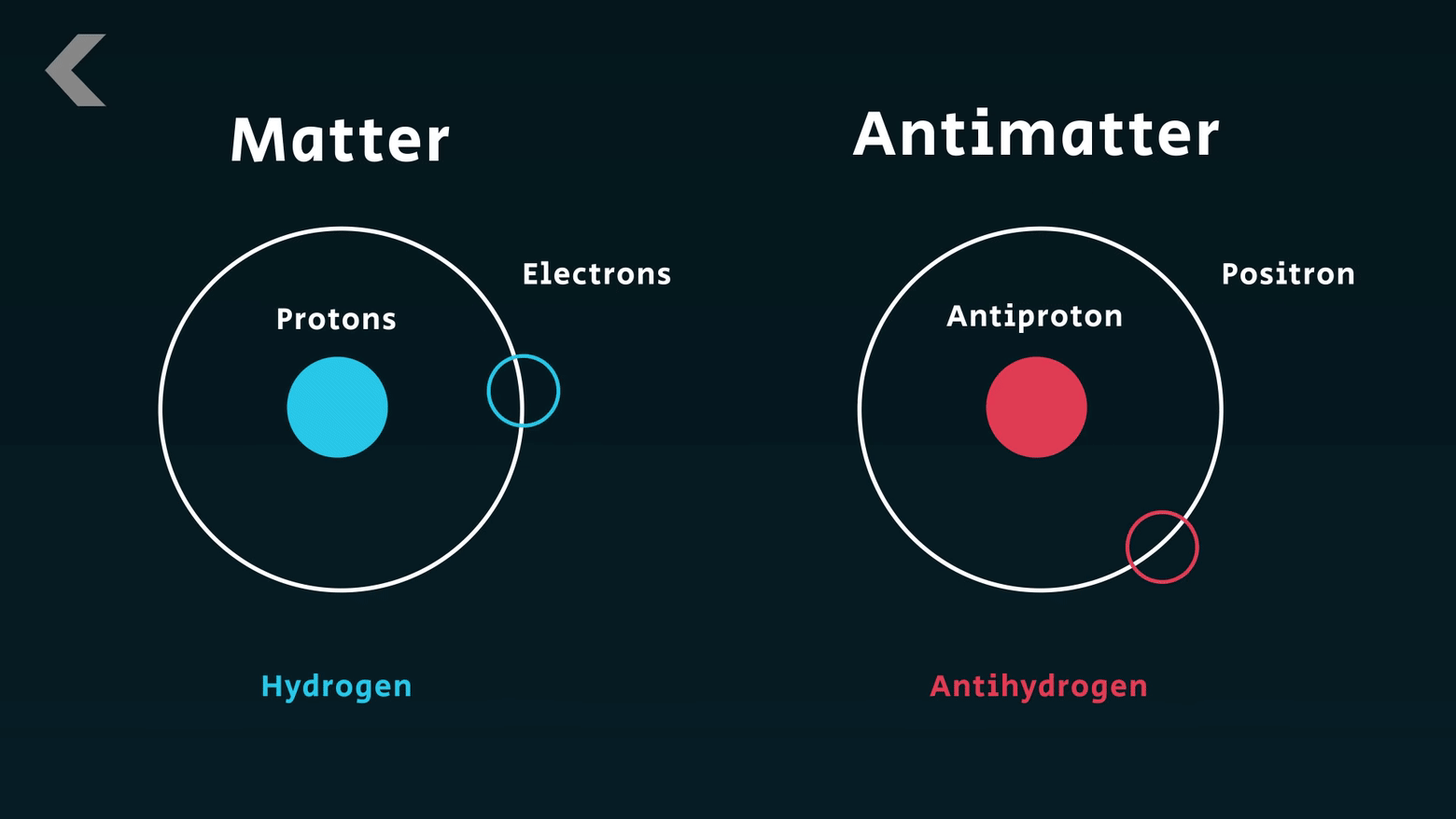
바로 -의 전하를 지닌 전자와 질량 전하량 등은 같지만 +의 반대 전하를 지닌 양전자 말입니다.
이뿐만이 아닙니다.
두 입자가 서로 만나게 되었을 때도 유추해볼 수 있겠죠. 앞서 에너지를 받고 양의 에너지 쪽으로 들뜬 전자는 다시 받은 에너지만큼의 전자기파를 방출하며 비어있는 음의 에너지 쪽으로 내려앉으려 할 것입니다.
이것을 우리는 쌍생성 되었던 두 입자가 서로 만나 쌍소멸하며 전자기파로 변환되는 것으로 관측하게 되겠죠.
반물질의 개념은 여기서부터 시작하게 됩니다.
디랙의 방정식에 의하면 양전자는 전자의 반물질이 되는 것입니다. 이것은 디랙의 방정식이 상대성이론의 에너지-질량 등가원리와도 통하는 것임을 뜻합니다.
에너지가 물질이 되고 물질이 에너지로 변환되는 것 말입니다.
많은 분들이 이것이 터무니없는 이야기로 들리실 것입니다.
분명 가득 차 있는데 보이지 않는 음의 영역과 물질을 소멸시키는 반물질이 있다니...
당시 학계의 반응도 크게 다르지 않았습니다. 디랙의 말에 그다지 신경쓰지 않는 분위기였죠.
하지만 놀랍게도 디랙이 수학만으로 예측했던 이 입자는 1932년 미국의 물리학자 칼 앤더슨에 의해 실제로 관측되게 됩니다. 그가 우주에서 날아오는 방사선 (Cosmic rays)을 관측하던 중 전자와 함께 생성되었다 소멸하는 전하만 반대인 입자를 발견하였던 것입니다.
디랙의 이 놀라운 생각은 이후 몇 가지 문제점들이 보안 되어 현재 물리학 이론 중 가장 높은 정확도를 지닌 이론으로 발전되었으며, 칼 앤더슨이 관측하였던 반물질은 현재 입자가속기를 통해 인공으로 만들 수 있게 되었고, 모든 종류의 기본입자에 반물질이 존재한다는 것도 밝혀졌죠.
---------------------------------------------
1932년에 앤더슨(Carl Anderson, 1905~1991)은 우주에서 날아온 에너지가 큰 입자나 광자인 우주선(Cosmic ray)이 자기장 속에 들어 있는 안개상자의 납판에 충돌할 때 생성되는 입자를 연구하고 있었다.
앤더슨은 전자와 반대 방향으로 휘어지는, 양전하를 가지고 있는 것으로 보이는 질량이 작은 입자를 발견했다.
그 후 에너지가 큰 감마선을 이용하여 이 입자가 존재한다는 것을 확인한 앤더슨은 최초로 발견된 반물질인 이 입자에 양전자(positron)라는 이름을 붙여 주었고, 이 연구로 1936년에 노벨상을 수상했다.
충분한 에너지를 가진 감마선이 어떤 물질에 부딪히면 전자-양전자 쌍을 만들어낸다.
에너지가 질량을 가진 입자로 변환된 것이다.
필요한 감마선의 최소 에너지는 아인슈타인의 공식인 E감마선=m전자 c2+m양전자 c2에 의해 결정된다.
전하를 가지고 있지 않던 감마선이 음으로 대전된 전자와 양으로 대전된 양전자를 생성하기 때문에, 전하가 보존되는 것이다.
양전자는 중성자의 수가 부족한 동위 원소의 방사성 붕괴시에도 방출된다.
예를 들어 안정한 탄소 동위 원소는 여섯 개의 양성자와 여섯 개 또는 일곱 개의 중성자로 구성된 12C나 13C의 형태로 존재한다.
앞에서 설명한 것처럼 14C는 전자를 방출하며 붕괴한다.
중성자들 중 하나가 전자와 반중성미자를 함께 방출하고 양성자로 바뀌는 반면에 다섯 개의 중성자만 가지고 있는 11C는 양전자를 방출한다.
즉, 양성자들 중 하나가 양전자와 중성미자를 방출하고 중성자로 바뀐다.
양전자가 어떤 물질에 부딪혔을 때는 양전자와 전자가 함께 소멸하여, 두 개의 감마선을 만들어낸다. 질량을 가진 입자들이 에너지로 변환된 것이다.
이 경우에도 아인슈타인의 공식, E감마선=m전자 c2+m양전자 c2이 생성된 감마선의 총 에너지를 구하는 데 사용될 수 있다.
반양성자는 가속된 입자가 금속 물질에 부딪히는 가속 장치에서 생성된다.
이 경우에는 우선 감마선이 방출되고 이 감마선이 이번에는 양성자-반양성자의 쌍을 생성한다.
반물질이 바티칸을 파괴할 수 있을까?
댄 브라운의 소설 《천사와 악마》에서 CERN의 물리학자들은 0.25g의 반물질을 만들기 위해 대형 하드론 충돌 가속기(LHC, Large Hadron Collider)를 사용한다.
소설에서는 바티칸을 파괴하려는 사람들이 이 반물질을 훔친다.
만약 0.25g의 반물질이 같은 양의 물질과 함께 완전히 소멸된다면, 이때 나오는 에너지의 양은 히로시마를 파괴한 폭탄의 에너지와 같을 것이다.
하지만 10년 이상 실험을 통해 오직 1000만 개의 반양성자만 검출할 수 있었으며 몇 초에서 몇 달 동안만 저장할 수 있었다.
0.25g은 반양성자의 1016배나 되는 많은 양이다. 게다가 반양성자는 극도로 낮은 온도에서, 완전히 비어 있는 ‘용기’에 저장해야 한다.
그리고 그보다 더 중요한 사실은 LHC는 반양성자를 생성하는 데 사용되지 않는다는 것이다.