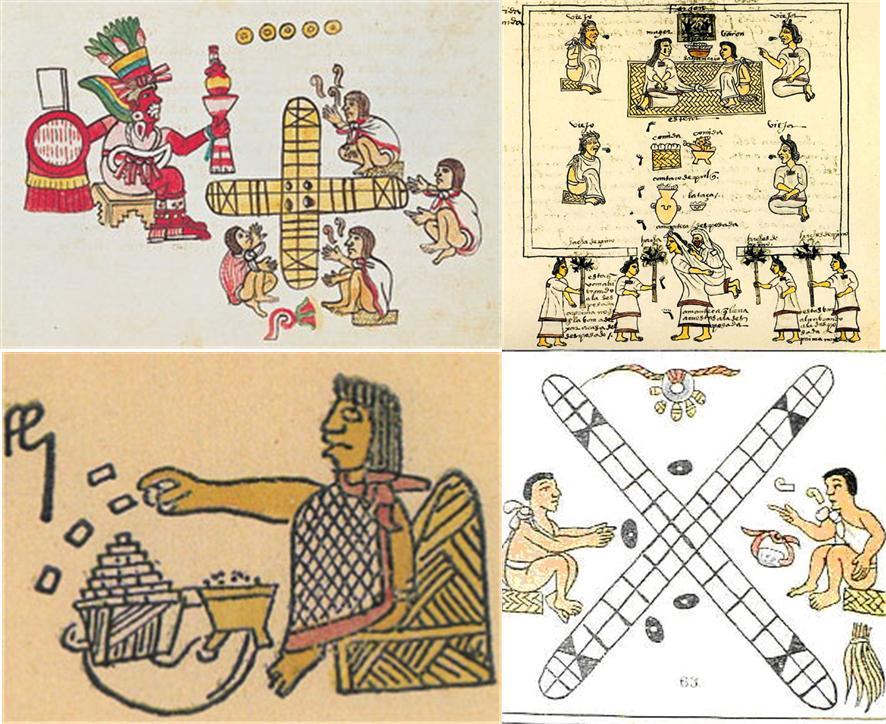
우리의 윷놀이와 유사성을 가진 대표적인 놀이로는 중국의 저포, 인도의 파치시Pachisi, 아스텍의 파톨리Patolli를 들 수 있다. 그리고 기타 학계에 보고된 아메리카 토착민들의 윷놀이형 유희의 사례로는 오클라호마의 교오와Kiowa 부족, 애리조나의 백산아파치부족, 파파고부족, 호피족, 뉴멕시코주의 티구아부족, 남아메리카 파라과이 볼리비아의 챠코Chaco부족, 마야문명의 후예인 북과테말라의 케치Kekchi족의 윷놀이가 있다.
윷가락 모양이 우리 것과 같으며, 대개 네 짝을 던져 나온 모습으로 점수가 매겨진다. 특히 케치족의 윷놀이는 우리의 윷놀이(콩윷)와 가장 닮았다.
케치족은 옥수수알 4개를 윷짝으로 대신하는데 일면은 숯으로 흑색을 만들어 자연색인 황색과 더불어 황흑2면이 되게 만든다. 4흑이 나오면 4점, 4황이 나오면 5점, 3황이 나오면 3점, 2황이 나오면 2점이 된다고 한다. 말은 다섯 개씩이며 판은 옥수수자루 열 개를 도열하여 놓은 것이다.
한반도에서와 같이 먼저 윷알을 던져 누가 먼저 시작하는가를 결정한다. 즉 점수가 높은 자가 먼저 시작한다. 말을 놓을 때 A와 B는 다른 방향에서 시작하며 먼저 놓은 말을 앞으로 옮겨도 되고 새로 놓아도 좋다. 한 집에 자기 것 둘을 넣을 수 없으며, 점수에 따라 A가 B의 말을 덮치면 그 말을 엎고 나가 포로는 자기 출발점으로 돌아가게 된다. (…) 이 승부에 참여하는 사람들의 열기는 대단한 것으로 한판승부에 보통 2~3시간이 걸린다 하며 던지기 전에 자신이 원하는 점수 이름을 대며 “모 나와라”, “모 나왔다”하는 식으로 떠든다는 것이다.1
19세기말의 영국의 석학 테일러E.B.Taylor는 윷놀이의 미주 전파론을 주장했다. 그는 멕시코와 북미인디언에서도 윷짝과 윷알이 공존하는 사례를 들면서 아시아에서 우선 멕시코로 전파되고 다시 북쪽으로 올라가면서 판이 없는 윷알놀이로 변화하는 것이 아닌가 상정하였다. 이에 대해 미국의 인디언문화 연구자이자 세계 놀이전문가인 컬린의 반론이 나왔고 이 두 가지 논論을 놓고 문화인류학자 간에 1950년대까지 설왕설래가 있었다.
컬린은 놀이의 전파성 문제보다 기원문제가 더 본질적인 것이라고 보았으며, 아스텍의 파톨리는 전적으로 아메리카에서 기원한 것으로 보았다.
윷놀이형 유희의 남아시아 인도대륙 기원설을 주장한 방선주는 나무윷짝과 윷알과 판이 결부된 부족은 미국 서남부와 멕시코일대에 밀집하고 있다고 말하면서, 다음과 같은 의문을 제기하고 있다.
어떻게 하여 양면체 윷짝을 흑백으로 호칭하는 것이 중국을 포함한 많은 지방에서와 북미 각 부족에서 공통될 수 있는가? 왜 ‘윷’이나 ‘모’가 나오면 다시 던질 권한이 있는 점이 같은가. 또한 적의 말을 잡으면 완전히 죽는 것이 아니라 재출발시키는 점도 그렇게 비슷할까. 어떻게 파톨리의 십자형판과 인도의 파치시, 쵸퍼chaupar의 판이 그렇게 흡사한가. 어떤 이유로 미주 각 지방의 윷짝이 한국의 그것에 닮을 수 있는가. 아울러 어떤 부족의 주마법走馬法이 한국의 그것과 신통히 닮았는가. 이것이 전부 자연발생적인 것인가? 자연발생하면 자연히 인도의 파치시형, 한국의 윷놀이형으로 발전하게끔 되어 있는가? 어떠한 이유로 현재 유행하는 백가몬Backgamon형으로 발전 못했는가? 이 놀이의 원형이라고 할 수 있는 아랍제국의 Tab-류의 윷짝은 한국의 윷짝과 같고 나오는 채수采數도 한국 것과 99% 같은 것이다.
그 중에서도 가장 중요한 초점은 왜 하필 양면체 윷짝으로 이어져야 하는가. 신대륙이면 신대륙답게 격절된 땅이면 새로운 척채법擲采法 계산법이 있을 만한 것이 아닌가. (…) 이상의 입론에 의하여 필자는 미주의 윷놀이가 동부아시아에서 역사시대에 전파되었다고 간주한다.2
거대해양을 사이에 두고 격절된 두 대륙에서 행해지는 놀이의 경탄할만한 유사성에 대한 방선주의 문제제기가 놀이의 기원성문제보다 전파성의 문제로 귀결되는 것은 충분히 납득할 만한 것이다. 하지만 그의 인도기원설에 선뜻 동의하기는 쉽지 않다.
파톨리는
아스텍 언어로 ‘납작한
콩’이라는
뜻으로 흰 점이 있는 검은 파톨리 콩 네 개를 던지며 노는 놀이다.
우리의
콩윷과
고고학적 자료들은 파톨리가 아스텍 시대 이전부터 마야인들과 멕시코 중앙 지역의 인디언 문화 속에 있어왔음을 보여주고 있다. 스페인들이 정복해 들어오기 이전 이 지역에 콩과 갈대를 사용하는 윷말 게임이 많이 퍼져 있었다.
아스텍 파톨리
파톨리가
처음 언급된 것은 16세기경이었다.
1521년
유럽의 정복자인 가톨릭 신부들은 파톨리게임을 미신과 우상으로 치부하여 금지하는 법령을 시행했고,
그
와중에 놀이판과 부속품들이 아스텍의 문서들과 함께 불탔다.
아스텍
보드게임인 파톨리는 언제 어떤 과정으로 만들어진 게임인지는
불분명한 채 아직
아스텍의 시간 주기는 52년을 단위로 하는데, 파톨리 놀이판에도 말을 놓는 자리가 52개다.
멕시코 볼라도레스
멕시코 놀이 중의 하나인 볼라도레스voladores도 숫자 52와 관련이 있다. 볼라도레스는 스페인어로 “(공중을) 나는 사람들”이란 뜻인데, 높이 세운 기둥 꼭대기에 묶은 줄에 4사람이 매달린 채 천천히 13번을 회전하여 땅에 닿는다. 4와 13을 곱한 값이 52이다. 이 52년 주기는 해年들의 한 ‘묶음’으로, 아스텍인들은 이 시간의 ‘묶음’들의 하나가 끝날 때 새로운 시기가 시작된다고 믿었다.
따라서 파톨리는 천체의 움직임과 그 기간 곧 아스텍의 역법과 관계가 있으며, 우리의 윷놀이처럼 점술의례적인 기능과 종교적인 의미가 담긴 놀이로 추측되고 있다.
우리는 고구려나 그 이전 시대의 발달된 천문학이나 역법에 관한 귀중한 자료들이 멸실되어 그 전모를 자세히 알 수 없는 상황이므로 마야나 아스텍에서 구축했던 고도의 지식들에 대한 상식을 가질 필요성이 있다.
아스텍 문명이 개발한 천문학, 역법의 체계는 상상을 초월한다. 태양의 피라미드 규모는 이집트 대 피라미드보다 더 거대하면서 각 변의 길이 방향의 오차율 역시 이집트 대피라미드처럼 0.001%의 오차율을 기록하고 있다.
그들은 매 1달을 20일로 하였다. 그래서 13개월로 이루어지는 260일력과 18개월로 이루어지는 365일력을 같이 사용했다. 365일력에서는 연말에 또 5일을 가하여 금기일禁忌日로 하였는데 합계는 365일이다. 달력은 촐킨tzolkin이라고 하는데 1년의 시간을 365.2420일로 계산하였다. 현대의 역법으로 보면 365.2422일인데 현대에 이르기까지 전 문명권을 합쳐서 가장 정확한 수치라고 한다.
260일력과 365일력으로 이루어지는 역법체계는 52년을 순환기로 한 번씩 겹친다.3 여기서 파톨리의 숫자 52가 도출되며, 파톨리게임이 종교적인 비전秘傳과 관련이 있다고 평가되는 이유이다.
마야나 아스텍인들이 왜 숫자 52를 중시했을까? 그리고 매 1개월을 20일로 해서 13개월로 이루어지는 260일력을 병용했을까?
(한 연구에 따르면, 아스텍인들은 1,366,560이라는 ‘초超 숫자’를 만들어냈는데, 이 숫자는 현 시대(아스텍인들이 구분한 시대 중 다섯 번째 태양의 시대)의 시작이 금성의 탄생으로 출발했다는 것을 암시하며, 다음과 같이 넓은 범위에 걸친 주요한 시간 주기들과 연관되어 있다는 것이다.
1,366,560 = 260 × 5,256 (촐킨의 수)
365 × 3,744 (공년의 수)
584 × 2,340 (금성의 평균주기 수)
780 × 1,752 (화성의 평균주기 수)
18,980 × 72 (달력 주기 곧 아스텍 세기의 수))
아스텍의 숫자 13, 4, 52는 동양의 역법체계에서 볼 때, 지구가 가만히 정지해 있을 때 달이 지구 주위를 공전하는 데 걸리는 시간인 1항성월과 관련이 있다. 현재 1항성월은 27.32일이다. 여기서 28수宿가 나왔다. 만일 한 달을 28일로 가정한다면, 1년 365일은 13개월에 하루를 더한 것과 같다(365 = 28 × 13 + 1) 한 달 28일은 7요曜에 4를 곱한 수이다. 28에 13을 곱한 값인 364는 52에 7을 곱한 값과도 동일하다. 따라서 이 관계는 다음의 등식으로 표시된다.
13 × 28 = 364 (1항성월 28의 13배수 364)
= 13 × 4 × 7
= 52 × 7
실제 아스텍인들이 이러한 역법까지 고려하여 13, 4, 52수를 중시하였는지는 알 수 없다.4 그러나 윷놀이와 파톨리의 유사성을 감안할 때 이러한 점이 전혀 고려되지 않았다고 단정하기도 어렵다.
리브 버빅Lieve Verbeec은 논문 ?불게임: 마야 저지대의 파톨리게임(Bul: A Patolli game in Maya lowland)?(1898)에서 파톨리게임에 대하여 다음과 같이 풀이했다.
1. 윷: 양면을 사용하는 네 개의 윷은 고대 인디언들의 시간에 사용한 파톨 콩의 성격과 그 숫자가 일치한다.
2. 점수내기: 표시가 된 부분 하나마다 1점
3. 점수 내는 방법: 네 개의 윷을 던져 5의 의미를 강조하는데 5수는 상징적 종교의 의미가 있다.
4. 팀 게임: 항상 같은 수의 두 팀이 붙었다.
5. 잡기: 상대를 잡으면 잡은 쪽의 말로 갈아놓는다.
6. 윷말판: 모양이나 길이를 막론하고 각 팀은 윷말판에 들어가는 자신들만의 입구를 결정할 수 있다.
7. 상대팀의 앞서가는 말을 잡는 것이 가장 흔하고 중요한 룰의 하나였다.5
이상에서 살펴보았듯이 파톨리는 놀이판 모양을 제외하고는 우리의 윷놀이와 놀이방법이 거의 동일하다. 특히 네 개의 콩윷을 던지고 다섯(모)의 의미가 강조되는 점에 있어서는 두 놀이가 같은 사상을 가진 것으로 보아도 무리가 없을 것이다.
??마글리아베치Magliabecci 코덱스??에 의하면 파톨리의 신은 가무와 놀이의 신인 마쿠일소치틀Macuilxochitl이며, 다섯 꽃의 신God of the Five Flowers으로 불렸다. 이것은 우리 윷의 점수체계인 오채五采와 동일하며, 오행이나 오행성과 이어지는 수리다.
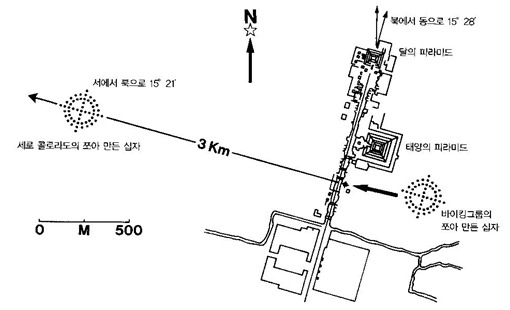
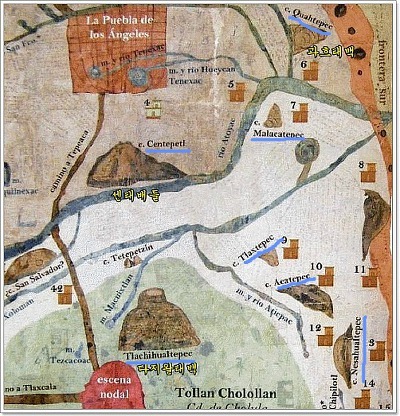
우리의 윷놀이와 파톨리게임 사이의 유사성 문제는 놀이의 차원에서만 머물지 않는다. 한반도와 집안 지역에서만 발견되는 것으로만 알았던 윷판형 유적이 아메리카대륙에서도 발견되었다는 보고가 있는 것이다. 서구 학계에서 십자형암각화(쪼아 만든 십자pecked cross) 라고 명명된 수십 개에 이르는 유사 윷판형 유적들은 대개 두 개의 원과, 원을 가로지르는 두 개의 축으로 4등분된 한 벌의 동심원이다.6 그것은 불교의 만다라 구조를 연상케 하는데 그 도상의 일부가 우리의 윷판과 완벽히 일치하는 것도 있다. 게다가 그것이 발견된 지역이 파톨리게임이 행해진 마야 아스텍문명의 중심지인 테오티우아칸 신전 부근이라는 사실은 우리를 더욱 놀라게 한다.
그림12 아메리카대륙에서 발견되는 십자형암각화
테오티우아칸 부근에서 발견된 두 개의 윷판형 유적은 서로 3㎞ 이상 떨어져 있는데, 방위를 결정하는 두 개의 십자를 연결하면 신전유적을 구성하는 가장 중요한 지형물에 수직으로 교차하는 선을 정해준다. 우리의 윷판형암각화들의 십자도 북두칠성의 방위와 연관이 있음을 보여주는데, 이로 보아 아시아 아메리카 두 대륙의 윷판형 유적의 제작자들은 십자형으로 천문이나 지형의 방위를 정하는 지식을 공유하고 있었음을 알 수 있다.
테오티우아칸 부근의 두 윷판형 유적은 다음과 같은 특징을 갖고 있다.
모두 지름이 90㎝인 두 개의 동심원으로 이루어져 있으며, 십자의 두 팔은 바위에 새기거나 바닥을 쪼아낸 일련의 얕은 구멍들이 동일하게 각각 18개씩이다(혹은 팔에 의해 나뉜 원에 있는 구멍까지 계산한다면 20개다). 또 팔의 구멍 패턴도 같다. 즉 안쪽 원의 내부에 10개, 원과 원 사이에 4개, 그리고 바깥 원 밖에 4개다.7
그림13 테오티우아칸의 십자형암각화(??고대하늘의 메아리?? 그림)
이 윷판형 유적의 도상에서 내부 동심원과 십자를 이루는 29점의 모양은 우리의 윷판형암각화와 똑같다. 바깥을 이루는 24점을 추가하면 전체적으로는 53점을 이룬다. 바깥의 24점은 24절기의 수리와 연결되고, 53점은 1년 52주의 수리에 근접하지만 정확히 무엇을 가리키는 것이라고는 단정할 수 없다. 하지만 우리의 윷판에서 천원점을 제외하면 28수의 수리가 나오듯이, 이 두 가지 윷판형 유적 또한 천원점을 제외하면 52수리가 나온다. 만일 그러한 점까지 고려하여 도상을 만들었다면 우리와 아스텍 윷판형 유적 중 디자인 창안의 선후가 어떤 것이라고는 잘라 말할 수 없지만 아스텍의 것이 우리의 것보다 포괄적인 의미를 나타내는 디자인이라고는 말할 수 있다.
그림14 테오티우아칸 전경 복원도(그림출처:commons.wikimedia.org)
고대 메소포타미아 지역의 수메르 전승에 따르면 태양이 새로 부활하는 우주운동의 한 주기가 시작되는 새해의례 기간의 처음 3일간 태양신으로 추앙받은 마르둑이 혼돈과 죽음의 지하세계에 잠시 머무르고 있음을 상징하는 뜻으로 거대한 피라미드 구조의 신전탑(지구라트) 안에 감금되어 있는데, 그 신전탑을 산山이라 불렀다고 한다.9 여기서 우리는 환웅이 내려온 태백산에 대한 암시를 얻을 수 있을지도 모른다. 태백산을 일명 방홀산方忽山ㆍ무엽산無葉山ㆍ백악산이라 부른다는 ??삼국유사??의 기록이나 ‘천해금악삼위태백’이라 한 ??태백일사??의 표현에서 그것이 피라미드 신전을 가리키는 것이라고 추측한 박용숙의 주장은 의미하는 바가 크다.10 그렇게 보게 되면 신단수는 신전탑의 의미와 통하며, ??규원사화??의 ‘천부삼인을 태백산 위에 있는 늪 옆 석상단목하石上檀木下에 둔다’는 기록의 의미도 이해할 수 있게 된다.
터키 괴베클리 테페(위)와 멕시코의 태백 지도(아래)
또한 이러한 수메르-바빌로니아 전승에서 설날의 어원에 대한 암시를 받을 수 있다. 설은 태양을 뜻하는 ‘ㅅㆍㄹ’ 또는 아직 덜 영글거나 익숙치 못해 생경하다는 뜻으로 사용되는 ‘낯설다’ ‘설익다’의 ‘설’에서 왔다는 주장도 있는데, 이것은 태양신 마르둑의 정초 3일간의 신전탑 감금 전승의 상징의미와 같은 것이다. 설달이 변해서 된 섣달인 축월丑月도 성숙되지 않은 달의 뜻을 지니고 있는데, 이는 태양이 어느 정도 익게 되는 정월(寅月) 직전의 달이기 때문이다. 이렇게 볼 때 새 태양의 건강한 부활을 기원하는 제야의 세수풍습이 지닌 의미와 설날의 어원에 대한 의문점이 함께 풀릴 수 있다.
해와 달이 뜨고 지는 지상의 방위와 관련하여 축조되는 피라미드는 그것이 위치한 곳을 천하의 중심-배꼽-으로 신성하게 여기도록 하는 기능을 함축하고 있다. 피라미드는 2분2지 때에 중요한 일월성신의 뜨고 지는 방위가 각인되어 있어야 할 것이며 건축물의 구조에도 정확한 천문역제의 수리가 내포되어 있어야 할 것이다.
고구려 장군총은 그러한 천문역제의 기능을 갖춘 것 중의 하나다. 계단식 피라미드형인 장군총은 7층으로 이루어져 있다. 그것은 왜 7층일까? 이 의문점에 대한 풀이는 카스티요 천문대의 구조적 특징과 함께 앞으로 살펴볼 것이다.
원문: <천부윷의 재발견>