환웅수학의 원방각과 오일러의 다면체정리와 오일러공식과는 어떠한 관계가 있을까요?
결론적으로 아주 중요한 관계가 있습니다.
오일러 다면체정리는
원방각의 내적인 수관계방식을 정립한 것입니다.
오일러 공식은 원방각을 길이로 환산 한 것입니다.
원방각의 버수라고 합니다.
오일러가 환웅수학의 수호자라고 할 수가 있습니다.
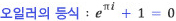
-----------------------------------------------------------
원방각과 오일러 다면체의 비교
원방각의 기본상수:
34= 3(각)* 4(개)+ 4(선)*4개+ 5(면적)+ 1(전체)
위 34의 수는 부도역의 상수입니다.
이는 간단한 기하학의 모형으로 환산하면...
아래의 정사각형에 해당합니다.
이제 원방각의 수와 오일러의 다면체 정리와 비교하면...
원방각과 꽂지점( 브이)와 모서리(이) 면(에프)와는 약간차이가 있습니다.
즉 원방각과 대응하는 점선면의 차이가 있다는 것입니다.
원= 점 방= 선, 각= 면에 해당합니다.
원- 점- 3
방- 선- 4
각-면- 5
위와같이원방각과 오일러의 기하학과는 약간 그 개념을 다릅니다.
문제는 간단합니다.
원= 3이고 방= 4이고 각= 5인 것이 맞습니다.
오일러의 다면체 정리에서
구와 연결 상태가 같은 다면체에서는 각(꼭지)의 개수(Vertics) - 방(모서리) 개수(Edge)+원(면)(Face)의 개수=2라는 오일러 정리가 성립한다.
v−e+f=2v−e+f=2
다면체는 다각형을 면으로 이루어진 입체도형이다. 중학교 1학년에서 배우는 다면체로는 크게 정다면체, 각기둥, 각뿔, 각뿔대로 나뉜다.
우선 정다면체의 구조를 파악해보자. 정다면체에 사용된 각각의 정다각형, 한점에 모인 면의 개수, 면의 수, 모서리의 수, 꼭짓점의 개수를 정리하면 아래와 같다.
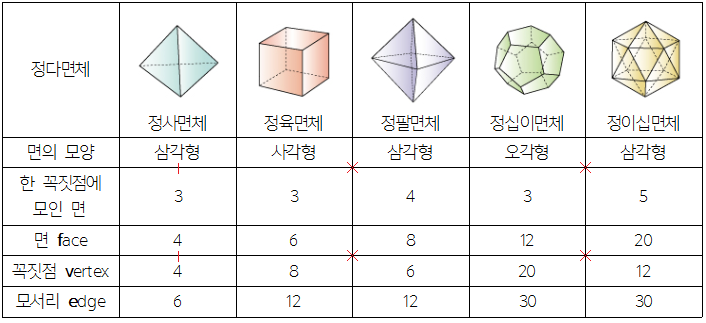
특히 모서리의 개수를 일일히 세다보면 굉장히 헷갈리다. 이를 면의 모양과 면의 수를 이용하여 쉽게 계산할 수도 있다.
정십이면체의 모서리 개수는
정오각형의 변의 수가 5개이고,
총 면의 수 12개 이고,
겹치는 모서리의 수 2개 이므로 5*12/2=30으로 총 모서리수의 수는 30개이다.
이와 같이 정이십면체의 모서리의 개수는
정이십면체의 꼭짓점의 개수는
정삼각형의 변의 수 3
총 면의 수 20
한 꼭짓점에 모이의 면의 개수 5 이므로 3*20/5=12이다.
반면 n각기둥, n각뿔대, n각뿔의 총모서리개수와 총 꼭짓점수, 총 면의 수를 정리하면 아래와 같다.
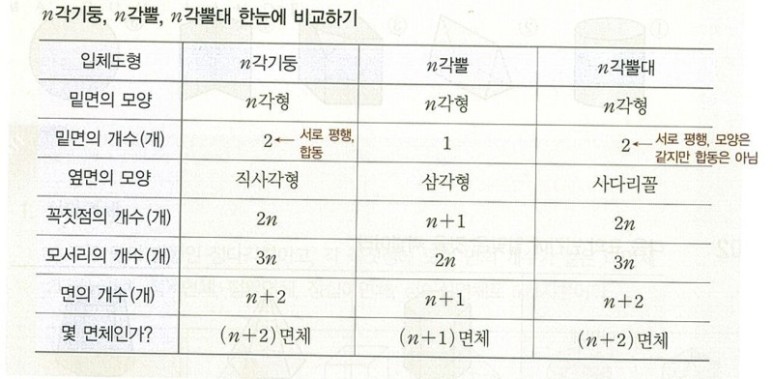
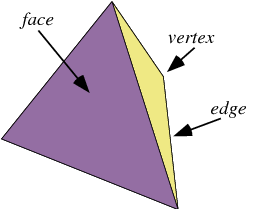
우리는 이렇게 총 8가지의 다면체의 모서리 개수와 면의 수, 꼭짓점수를 알아보았다. 그렇다면 이 세개의 항목을 이용하여 덧셈 뺄셈을 이용하여 상수를 만들 수 있다. 어떤 공식을 만들 수 있을까?
혹시 오일러 공식을 들어보았는가?
(꼭짓점의 개수) + (면의 개수)-(모서리의 개수)=2 라는 것을 우리는 쉽게 확인 할 수 있다. 오일러는 꼭짓점의 개수는 v(vertex)라 하고, 모서리의 수를 e(edge)라 하고, 면의 수를 f(face)할 때 v-e+f=2 라 하였다. 이것이 바로 오일러 공식이다. 들어본 아이들은 금방 만들었다. 그리고 모든 다면체에서 이 공식은 성립한다. 이때 2를 오일러의 수라고 한다.
오일러는 사실 한붓그리기와 관련이 있는 유명한 수학자이기도 하였고, 위상수학의 개념인 도넛과 손잡이가 있는 커피잔이 서로 같다라는 이야기도 하였다.
그렇다면 오일러의 공식을 평면도형의 적용하여 보자.
삼각형의 오일러의 수를 구하면 (꼭젓점의 수) + (면의 수)- (변의 개수) = 1임을 확인할 수 있다. 이는 모든 다각형에서 마찬가지로 1임을 확인할 수 있다.
이렇게 변화하는 과정 안에서도 결국 변하지 않는 양을 불변량(invariant)이라 한다. 또다른 대표적인 불변량으로는 다각형의 외각의 합이 있다. 이렇듯 오목이든 볼록이든 모든 다각형의 외각의 합은 360이다. 이를 다면체로 확장하면 도는 다면체의 외각의 합은 720도이다.
-----------------------------------------------------
오일러 공식
eix=cosx+isinx
$ei\pi +1=0$eiπ+1=0
eix=cosx+isinx
$ei\pi +1=0$eiπ+1=0
$\pi \ :\ 원주율$π : 원주율
$\iota \ :\ -1의제곱근,\ 허수$ι : −1의제곱근, 허수
$\e \ :\ \pi 처럼\ 순환하지\ 않은\ 무리수\ 수학에서\ 가장\ \ 중요한\ 정수의\ \ 하나$℮ : π처럼 순환하지 않은 무리수 수학에서 가장 중요한 정수의 하나
$\log :정수를\ 몇제곱해서\ 임의의\ 정수를\ 얻었을\ 때\ 제곱한\ 횟수,\ 정수는\ 밑이라\ 한다.\ $log:정수를 몇제곱해서 임의의 정수를 얻었을 때 제곱한 횟수, 정수는 밑이라 한다.
$\ \ \ \ \ \ \ \ \log _{10}\combi{100}=2$ log10100=2
$$
보통 10진 법의 세계에서는 편리하게 10을 밑으로 하는 로그함수를 사용하고 이를 상용로그라고 하는데, 수학 이론에서는 상용로그보다 e를 밑으로 하는 로그의 역할이 더 크다. e는 자연로그라고 하고 e를 제곱한 횟수를 지수라고 한다.
오일러가 산출한 e 값은
e=2.71828182845904523536028..........
$e=1+\frac{1}{1}+\frac{1}{1\times 2}+\frac{1}{1\times 2\times 3}+\frac{1}{1\times 2\times 3\times 4}+...........$e=1+11+11×2+11×2×3+11×2×3×4+...........
무리수인 자연상 수 e를 밑으로 허수 i 와 무리수 파이의 곱을 지수로 한 자연로그가 1과 더해지면 0이 된다. 오일러 공식에는 수학에서 가장 중요한 5가지 상수가 사용되었다.
$e,\iota ,\pi ,\Theta ,1$e,ι,π,Θ,1
그리고 지수, 곱셈, 덧셈, 등호 4가지 연산이 모두 쓰였다. , 누구도 상상하지 못한 순환하지 않은 무리수와 존재하지 않은 수의 조합에 1을 더해 0으로 규합시킨 오일러 공식이 세상에 가장 아름다운 공식이라 불리는 이유다.
이 멋진 공식은 나중에 캐서린 존슨이 착륙 좌표를 계산하는데 중요한 원리가 되어 우주 궤도 비행 프로젝트에 결정적인 역할을 하게 된다.