[25~27] 다음 글을 읽고 물음에 답하시오.
[네이피어의 막대]라고도 불리는 네이피어의 뼈는 곱셈을 쉽게 할 수 있게 해 주는 도구로 나눗셈, 제곱근의 계산 등도 쉽게 할 수 있다. 네이피어의 뼈는 모두 10개로 이루어져 있다. 막대의 한 면의 머리에는 0에서 9까지의 수 중 하나가 써 있고 그 아래 2번째 칸에서 9번째 칸에는 각 머리 수의 배수가 2배부터 9배까지 기록되어 있는데 대각선의 위에는 십의 자리가, 아래에는 일의 자리가 기록되어 있다.
[A] {네이피어의 뼈를 이용하여 12^16^7을 계산하기 위해서는 머리 수가 1, 2인 두 막대를 뽑아서 왼쪽에서 오른쪽으로 나란히 붙여 놓는다. 이로써 12를 표현한 것이다. 그 다음에는 7을 곱하기 위해서 막대의 7번째 가로줄의 숫자를 본다. 머리 수가 1인 막대는 0/7, 머리 수가 2인 막대는 1/4라고 적혀 있을 것이다. 이것을 이어서 쓰면 0/7 1/4가 된다. 이때 인접해 있는 7과 1을 더하면 8이 되므로 0/8/4로 적고, 이 곱셈의 답 84를 구하게 된다. 왜 이런 결과가 나오는 것일까? 그것은 각각의 막대가 각 막대의 머리 수를 배수로 하는 수를 적어 놓은 것이기 때문에 1의 7배수와 2의 7배수를 구한 다음에 앞에서 구한 수는 10을 곱하고 뒤에 구한 수는 1을 곱하여 더한 것임을 알 수 있다. 그러면 345^16^234를 계산해 보자. 이를 위해서 머리 수가 3, 4, 5인 세 막대를 뽑아서 왼쪽에서 오른쪽으로 나란히 붙여 놓는다. 계산을 단계별로 하기 위해서 먼저 345^16^2를 계산하는데 막대의 2번째 가로줄을 보자. 0/6 0/8 1/0을 볼 수 있을 것이다. 이웃한 수는 더해 주고 왼쪽부터 읽어 주면 0690이 되어 그 답이 690임을 알 수 있다. 345^16^3을 계산하려면 붙여 놓은 세 막대의 3번째 가로줄 0/9 1/2 1/5를 같은 방법으로 더해 주어 0/10/3/5를 얻되, 이렇게 10을 넘는 결과가 나오면 위의 자리로 올려서 더해 주면 되는데 1035가 답이 된다. 같은 방식으로 345^16^4를 계산하면 1/2 1/6 2/0으로부터 1/3/8/0, 즉 1380을 얻는다. 이제 앞서 구한 세 수 690, 1035, 1380을 첫 번째 수에는 100을 곱하고, 두 번째 수에는 10을 곱하고 세 번째 수는 1을 곱하여 더하게 되면
39000
10350
1380
80730
을 얻는다. 따라서 80730이 345^16^234의 답이다.
그러면 나눗셈은 어떻게 할까? 7^34,34^3을 계산해 보자. 나누는 수인 3을 머리 수로 갖는 막대에 적힌 수를 보면 3, 6, 9, … 순서로 되어 있다. 우리가 구할 7은 6과 9 사이에 있다. 6은 2번째 수이고 9는 3번째 수이다. 그러므로 여기에서 2를 얻는다. 소수점 아래의 값을 구하려면 7에서 3의 2배수인 6을 뺀 나머지 값인 1에 10을 곱하여 10을 얻은 후에 머리 수가 3인 막대에 몇 번째 가로줄에 10이 나타나는지 찾는다. 3번째 수가 9, 4번째 수가 12이므로 몫의 소수점 아래 첫 번째 수는 3이라고 말할 수 있다. 그래서 원하는 몫의 근삿값은 2.3이 된다. 만약 다음 소수점 아래의 수를 구하려면 이 과정을 반복하면 된다. 네이피어의 뼈를 이용한 이러한 계산은 35년 후 파스칼이 계산기를 발명하는 데 영향을 주었으며 컴퓨터의 개발에도 큰 도움을 주게 된다.
25. [네이피어의 막대]에 대한 설명으로 적절하지 않은 것은?
① 계산을 편리하게 하기 위한 보조 도구이다.
② 기계식 계산기와 컴퓨터의 개발에 큰 도움을 주었다.
③ 10개의 막대에는 각 막대의 머리 수의 배수가 적혀 있다.
④ 나눗셈을 할 때는 나누려는 수를 머리 수로 갖는 막대에서 나누는 수가 어디에 있는지를 확인해서 몫을 구한다.
⑤ 두 자릿수의 숫자를 곱할 때는 십의 자리의 수부터 단계별로 계산하여, 첫 번째로 구한 수에는 10을, 두 번째로 구한 수에는 1을 곱해 주어야 한다.
26. (보기) 는 네이피어 막대 7개를 붙여 놓은 것에서 하나의 가로줄을 보여 준다. 계산하려는 문제에 해당하는 것은?
(보기)
① 2348566×5 ② 4678539×4
③ 6238052×3 ④ 9357078×2
⑤ 18714156×1
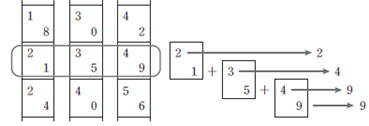
27. (보기) 는 [A] 를 읽은 학생이 네이피어 막대에 대해 발표하기 위해 만든 보조 자료이다. 이를 통해 학생이 설명할 네이피어 막대의 특징으로 가장 적절한 것은? [3점]
(보기)
① 간단한 덧셈을 이용해서 곱셈의 계산을 쉽게 할 수 있다.
② 덧셈의 원리를 활용하여 소수점 아래의 값을 쉽게 구할 수 있다.
③ 배수를 활용하여 근삿값을 찾기 때문에 곱셈을 빨리 할 수 있다.
④ 막대에서 제곱근을 찾아 더해 줌으로써 곱셈을 간편하게 할 수 있다.
⑤ 곱셈을 덧셈으로, 덧셈을 곱셈으로 바꾸어 복잡한 계산을 쉽게 할 수 있다.
도움자료
[2015 EBS 수능특강 B]
25~27.
‘네이피어의 뼈’
해제
이 글은 계산을 편리하게 하기 위한 보조 도구로서 존 네이피어가 고안한 ‘네이피어의 뼈’의 용도와 구성, 곱셈과 나눗셈의 방법에 대해 설명하고 있다. 네이피어의 뼈는 곱셈을 쉽게 할 수 있게 도와주는 도구로 10개의 막대로 구성되어 있다. 각 막대의 머리에는 0에서 9까지의 수가 적혀 있고 2번째 칸부터는 각 막대 머리 수의 배수가 적혀 있다. 네이피어의 뼈를 이용하여 곱셈을 하기 위해서는 계산하고자 하는 수를 머리 수로 하는 막대를 뽑아 나란히 붙여 놓고, 곱하는 다른 수에 해당하는 가로줄의 숫자를 찾는다. 이때 인접한 숫자들을 더하면 답을 구할 수 있다. 만약 곱하는 다른 수가 일의 자리가 아니라면 단계적으로 계산을 해 주면 된다. 나눗셈은 나누는 수를 머리 수로 갖는 막대에서 나누려는 수를 찾는데, 이때 나누려는 수가 두 숫자의 사이에 있다면 작은 수에서 몫을 얻고, 나누려는 수에서 막대에서 찾은 값을 뺀 나머지로 소수점 아래의 수를 구한다. 네이피어의 뼈를 이용한 이러한 계산법은 후에 계산기의 발명과 컴퓨터의 개발에 영향을 준다.
주제
네이피어의 뼈를 이용한 계산법과 그 영향
구성
• 1문단: 계산 보조 도구의 개발
• 2문단: 네이피어의 뼈의 용도와 구성
• 3문단: 네이피어의 뼈를 이용한 곱셈 방법
• 4문단: 네이피어의 뼈를 이용한 나눗셈 방법과 그 영향
25. 세부 정보, 핵심 정보 파악
[정답이 정답인 이유]
④ (실마리) 나누려는 수, 나누는 수
4문단에서 나눗셈의 계산을 위해서는 나누는 수를 머리 수로 갖는 막대에서 나누려는 수가 어디에 있는지 확인해서 몫을 얻는다고 설명하고 있다. 그러므로 나누려는 수를 머리 수로 갖는 막대에서 나누는 수가 어디에 있는지 확인한다는 것은 적절하지 않다.
[오답이 오답인 이유]
① (실마리) 편리, 보조 도구
1문단에서 계산을 편리하게 하는 보조 도구의 개발은 인류의 전 역사를 통해 이루어졌고, 복잡한 계산을 쉽게 할 수 있는 도구로 고안된 것이 네이피어의 뼈라고 설명하고 있다. 그러므로 네이피어의 막대가 계산을 편리하게 하기 위한 보조 도구라는 설명은 적절하다.
② (실마리) 계산기, 컴퓨터, 도움
1문단에서 네이피어의 뼈는 기계식 계산기의 토대를 놓았다고 설명하고 있으며, 4문단에서는 파스칼이 계산기를 발명하는 데 영향을 주었으며 컴퓨터의 개발에도 큰 도움을 주었다고 설명하고 있다. 그러므로 네이피어의 막대가 기계식 계산기와 컴퓨터의 개발에 도움을 주었다는 설명은 적절하다.
③ (실마리) 10개, 머리 수의 배수
2문단에서 볼 때, 네이피어의 뼈는 모두 10개로 이루어져 있으며 막대의 한 면의 머리에는 0에서 9까지의 수 중 하나가 써 있고, 그 아래 2번째 칸에서 9번째 칸에는 각 머리 수의 배수가 기록되어 있다. 그러므로 10개의 막대에는 각 막대의 머리 수의 배수가 적혀 있다는 설명은 적절하다.
⑤ (실마리) 단계별, 첫 번째 10, 두 번째 1
3문단에서 볼 때, 세 자릿수의 숫자를 곱할 때는 계산을 단계별로 하기 위해서 백의 자리의 수부터 계산한다. 단계별로 계산해서 각각의 값을 구한 후에는 첫 번째로 구한 수에 100을, 두 번째 수에 10을, 세 번째 수에 1을 곱하여 더함으로써 답을 얻는다. 그러므로 두 자릿수의 숫자를 곱할 때도 십의 자리의 수부터 단계별로 계산하여 구한 값에 각각 10과 1을 곱해 주면 되므로 적절한 설명이다.
26. 구체적 상황에 적용하기
[정답이 정답인 이유]
② (실마리) 4
3문단에서 볼 때, 12^16^7을 계산하기 위해서는 먼저 머리 수가 1, 2인 두 막대를 뽑아 왼쪽에서 오른쪽으로 나란히 붙여 놓고, 두 막대의 7번째 가로줄의 숫자를 통해 답을 구한다. (보기)는 7개의 막대를 붙여 놓은 것에서 하나의 가로줄을 보여 주는 것이므로, 네이피어의 막대에서 (보기)의 숫자들이 나타나는 가로줄을 찾으면 곱하는 수를 알 수 있다. 4번째 가로줄에 (보기)의 숫자들이 나타나므로 곱하는 수는 4, 막대에서 각각의 머리 수를 확인하면 4, 6, 7, 8, 5, 3, 9가 되므로 계산하려는 문제는 4678539^16^4이다.
[오답이 오답인 이유]
① (실마리) 5
(보기)의 숫자들은 네이피어 막대의 4번째 가로줄에 나타나므로 곱하는 수는 4이고, 순서대로 막대에서 각각의 머리 수를 확인하면 4, 6, 7, 8, 5, 3, 9가 되므로 2348566^16^5는 계산하려는 문제가 아니다.
③ (실마리) 3
(보기)의 숫자들은 네이피어 막대의 4번째 가로줄에 나타나므로 곱하는 수는 4이고, 순서대로 막대에서 각각의 머리 수를 확인하면 4, 6, 7, 8, 5, 3, 9가 되므로 6238052X3은 계산하려는 문제가 아니다.
④ (실마리) 2
(보기)의 숫자들은 네이피어 막대의 4번째 가로줄에 나타나므로 곱하는 수는 4이고, 순서대로 막대에서 각각의 머리 수를 확인하면 4, 6, 7, 8, 5, 3, 9가 되므로 9357078X2는 계산하려는 문제가 아니다.
⑤ (실마리) 1
(보기)의 숫자들은 네이피어 막대의 4번째 가로줄에 나타나므로 곱하는 수는 4이고, 순서대로 막대에서 각각의 머리 수를 확인하면 4, 6, 7, 8, 5, 3, 9가 되므로 18714156X1은 계산하려는 문제가 아니다.
27. 글의 주제, 함축된 의미 추론
[정답이 정답인 이유]
① (실마리) 덧셈을 이용, 쉽게
[A]는 네이피어의 막대를 이용하여 곱셈하는 방법에 대해 설명한 부분이고, (보기)는 이것을 시각적으로 보여 줌으로써 네이피어 막대의 특징을 단적으로 보여 줄 수 있는 자료이다. 즉 (보기)는 인접해 있는 숫자들을 더하여 곱셈의 답을 쉽게 구하는 과정을 시각적으로 보여 주는데, 이를 통해 네이피어 막대의 특징은 간단한 덧셈을 이용해서 곱셈을 쉽게 할 수 있는 것이라 설명하는 것은 적절하다.
[오답이 오답인 이유]
② (실마리) 소수점 아래의 값
(보기)는 [A]에서 설명하고 있는 네이피어 막대를 이용한 곱셈 방법을 시각적으로 보여 줌으로써 간단한 덧셈을 이용해서 곱셈을 쉽게 할 수 있는 네이피어 막대의 특징을 단적으로 보여 줄 수 있는 자료이다. 그러므로 소수점 아래의 값을 쉽게 구할 수 있다는 설명은 적절하지 않다.
③ (실마리) 근삿값
네이피어 막대의 1번째 칸에는 0에서 9까지의 머리 수가 써 있고, 2번째 칸부터는 그 배수가 기록되어 있지만 이를 활용하여 근삿값을 찾는 것과 곱셈의 계산은 무관하기 때문에 적절하지 않다.
④ (실마리) 제곱근
네이피어 막대에 적힌 수는 0에서 9까지의 머리 수와 그 배수이지 제곱근이 아니므로 막대에서 제곱근을 찾아 더해서 곱셈을 간편하게 할 수 있다는 설명은 적절하지 않다.
⑤ (실마리) 덧셈을 곱셈으로
(보기)는 [A]에서 설명하고 있는 네이피어 막대를 이용한 곱셈 방법을 시각적으로 보여 준 것으로, 그 특징은 곱셈을 덧셈으로 바꾸어 곱셈의 계산을 쉽게 할 수 있다는 것이다. 그러므로 덧셈을 곱셈으로 바꾸어 복잡한 계산을 쉽게 할 수 있다는 설명은 적절하지 않다.