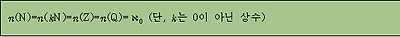<수업보조자료 6차시> 자연수의 개수=정수의 개수=유리수의 개수(2)

[mathmania]

두 집합 사이에 일대일 대응이 성립하면 두 집합의 원소의 개수는 같은 것이고, 이 때 ‘기수(基數)가 같다’고 말한다. 기수는 서수(序數)에 대응하는 개념인데 무한집합끼리도 일대일 대응만 성립한다면 두 집합은 ‘기수가 같다’라고 말하고, 이를 두고 좀 익숙한 용어로 ‘개수가 같다’라고 한다.

자연수 전체의 집합 N의 기수를 χ₀라고 나타내는데 히브리어 자모의 첫 글자를 알레프라고 하며, χ₀는 ‘알레프 널(aleph null)'이라고 읽는다. 무한집합의 기수를 초한기수(超限基數)라고 하는데, χ₀는 가장 작은 초한기수가 되는 것이다. 너무 어려운 말들이 나오니 힘들 것이다.

 

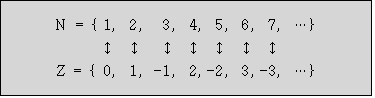
위에서 보듯, 집합 N과 정수의 집합 Z는 일대일로 대응시킬 수가 있다.

따라서 집합 N과 집합 Z의 기수는 χ₀로 같다.

 

위의 그림에서 이미 나타난 수를 제거하면서 화살표가 지시하는 대로 수를 나열하면(기약분수만 나열하면) 다음과 같은 무한 수열을 얻을 수 있다.

1, 2, 1/2, 1/3, 3, 4, 3/2, 2/3, 1/4, 1/5, 5, …

따라서, 자연수 전체의 집합과 양의 유리수 전체의 집합은 일대일대응을 시킬 수 있다.

이제 유리수 전체를 다음과 같이 배열해 보자.

0, -1, 1, -2, 2, -1/2, 1/2, -1/3, 1/3, -3, 3, -4, 4, -3/2, 3/2, -1/4, 1/4, …

위의 배열대로 자연수와 대응시키면 일대일대응이 된다. 따라서 유리수 전체의 집합과 자연수 전체의 집합은 대등하고 기수는 χ₀이다.

요약하면,

kN={kn|k≠0, n∈N}

Q: 유리수 전체의 집합

칸토어는 무한집합의 크기를 재는데 가산(Countable)과 비가산(Uncountable)의 개념을 도입했다. ‘가산’인 무한집합은 자연수의 집합과 일대일 대응관계가 있고, ‘비가산’인 무한집합은 그렇지 않다.

이를테면, 위에서 다루어진 의 배수의 집합과 정수의 집합, 유리수의 집합은 모두 가산집합이다.