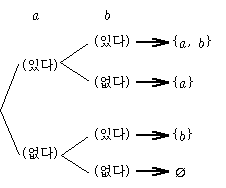<수업보조자료 6차시> 멱집합의 성질(2)

[mathmania]

두 번째 방법은 다음과 같은 수형도를 한 번 이용해 보자.

※이러한 방법을 편의상 <(있다), (없다)의 원리>라고 부르자.

이 방법으로도 네 개의 부분집합을 모두 구할 있으며, 수형도의 원리에 의하여 2×2=2² =4가지의 부분집합이 생긴다는 것을 알 수 있다.

이제 집합 X={a, b}의 멱집합을 구하면

P(X)={Φ, {a}, {b}, {a, b}}

이고, 멱집합 P(X)의 원소의 개수는 2²=4개이다.

주어진 집합 X의 원소의 개수가 n개라면 위의 두 가지 방법을 사용하면 2ⁿ개라는 사실을 쉽게 알 수 있다.

이제 무한집합의 경우가 남았다. 슬슬 긴장감이 돌기 시작한다.

집합 X가 무한집합이라면 위의 두 가지 방법은 무용지물이 된다.

더구나 무한집합의 멱집합이라고 하는 것을 상상하기 조차 쉽지 않다.

이제 보여주려고 하는 것은 결론부터 얘기하자면 무한집합의 멱집합은 원래의 무한집합보다 개수가 많다는 것이다. 정확하게 말하면 기수(농도)가 크다고 말해야 할 것이다.

집합 X를 무한집합이라고 놓는 것이 아니라 더 일반적으로 임의의 집합이라고 놓는 것이 좋겠다. 집합 X의 기수(the cardinal number of the set X)를 Card(X)라고 표현한다.