배반사건은
A와 B가 배반의 관계에 있다 가 A∩B=Φ 로 정의되고
이 집합의 관계를 벤다이어그램으로 그렸을때 시각적으로 다가와 쉽게 이해가 됩니다.
그러나 독립에 대한 정확한 정의가 와닿지 않습니다.
독립이 사건 a가 그 뒤에 일어나는 사건 b가 일어날 확률에 영향을 주면 종속 안주면 독립인거는 말로써 상식으론 이해하겠는데 그것을 정확한 정의로써 표현하려 하면 잘이해가 되질 않습니다.
질문1) 그런데 교과서에 두 사건이 독립이라는 말이랑 독립시행이라는 말이 있는데 그 차이를 모르겠습니다.
질문2) 사건이 독립인 것 모두는, 배반사건 처럼, 집합으로 시각적으로 표현할 수 있나요?
독립과 배반의 관계가 너무나 헷갈립니다. 마치 저에게는 둘이 배반사건이거나 배반사건이 아니거나 하여 공통된 부분이 있거나 없으면 그 여부가 서로에게 당연히 영향을 끼칠 것 같은 느낌이 들어 배반사건이면서 독립일 수도 있고 배반사건이 아니면서 독립일 수도 있다는 것이 부자연스럽게 느껴집니다.
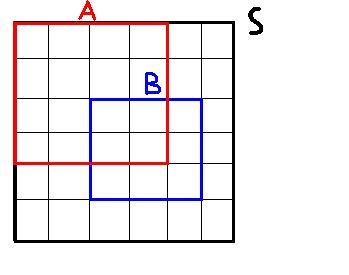
독립의 정의( P(A|B) = P(A|B^c) = P(A) ) 를 생각해보다가 이런 걸 그리게 되었는데
질문3) 제가 그린 그림에서 두 사건은 배반사건이 아니지만 독립사건입니다. 저는 그냥 생각을 하다가 이런 예를 찾아내게 되었는데 여기서 좀 이상한 점이 있습니다.
저는 독립이란 두 사건이 서로 확률에 영향을 끼치지 않는다는 추상적인 말로만 들었는데 이것을 실제로 집합으로 그런 말 없이 그릴수 있다는 점과(그러니까 독립사건이라는 것을 실제로 집합으로 표현이 가능하다는 것)
이것이 n(A):n(A∩B) = n(S):n(B) 라는 특별한 '비율' 을 가진 경우 그릴수 있게 된다는 것이 어떤 의미를 가지는지 알고 싶습니다. 왠지 배반과 독립사이의 제가 잘 이해하지 못하고 있는 끊어진 관계를 이을 수 있는 실마리가 여기 있다는 느낌이 들기 때문입니다.
저는 이과도 아니고 수학에 대해 잘 모르는 학생이다 보니까 제가 아예 맞다고 생각하고 글에 쓰게 된 점들이 실제로 틀렸어도 화내지 마시고 제가 잘 못 알고 있는 점을 너그럽게 알려주시기 바랍니다.
그리고 저는 저 관계가 너무나 궁금합니다. 그러니 이 질문들에 대한 답변을 저에게 주시면 아주 감사할 것입니다. 감사합니다.
댓글
댓글 리스트-
답댓글 작성자sodong 작성시간 11.01.21 이 댓글 확인하면 쪽지로 학생의 실명 좀 알려주세요. 책에 딸랑 닉네임만 들어가는 것보다는 본인의 이름이 들어가는 것이 더 보기 좋잖아요. ^^
-
작성자RipVanWinkle 작성자 본인 여부 작성자 작성시간 11.01.21 그나저나 저는 부끄럽게 아직 수학의 재구성을 아직 완독하지 못했는데 이번기회에 확실히 완독하고 한번 더 봐야겠네요. 소동님 감사합니다.
-
작성자RipVanWinkle 작성자 본인 여부 작성자 작성시간 11.01.21 위의 말은: 고등학교에서 배우는 독립사건은 그저 "추상적"으로 ; '일어났을때 서로의 확률에 영향을 끼치지 않는것' 이라고 배웠는데, "어떻게" 원소의 갯수의 비율n(A):n(A∩B) = n(S):n(B) 에 의해 독립이라는 관계가 정의될 수 있는가? 라는 질문이었습니다.
-
작성자RipVanWinkle 작성자 본인 여부 작성자 작성시간 11.01.21 결국 n(A):n(A∩B) = n(S):n(B) 이 왜 두 사건이 독립임을 의미하는가? 에 대한 질문이었습니다. 글로 표현하려니 전에는 너무 횡설수설했군요.
-
작성자RipVanWinkle 작성자 본인 여부 작성자 작성시간 11.01.21 401쪽 부터 409쪽까지 정독한 뒤 혹 또다시 질문이 생기면 질문하겠습니다. 소동 선생님 감사합니다.