[6.0] Computer Architecture - 진수체계 이해하기
컴퓨터보단 수학에 가까울 수도 있습니다만, 컴퓨터를 이해하는 데에
반드시 필요한 개념 중 하나인 '진수체계'에 대해 다뤄보도록 하겠습니다.
컴퓨터는 내부적으로 2진수 체계로 동작합니다. 물론, 인간에게 표시(display)할 때는
편의상 10진수, 혹은 문자로 표현할 지도 모르죠.
예를 들어 'A' 라는 문자는 ASCII(ANSI 표준) 코드로 나타내면 &H41(16진수) 인데, 이는 10진수로 65이고,
이진수(binary)로 0100 0001 의 값을 갖습니다. 이 때 컴퓨터는 내부적으로 0100 0001 와 같이 비트체계로
표시하여 나타냅니다. 비트(bit)란, 어떤 상태(참과 거짓)을 컴퓨터의 전기적 신호로 바꾼 on(1)/off(0) 것을
말하는 것이고, 1 byte는 8 bit입니다.
| 이것만은 알고 넘어갑시다:
bit는 전기적 신호의 일종으로, 0(Off)/1(On)의 상태만 가지는 값입니다. 컴퓨터의 메모리와 버스 체계는 비트 단위로 구성되어 있습니다. 메모리는 플립플롭(flip-flop)이라는 1bit 처리 단위의 기억 소자로 이루어져있고, 버스 체계 역시 비트 단위로 동작합니다. 그리고 1 바이트는 8개의 비트로 이루어져 있습니다. |
필자가 수학을 배울 때엔 중학교 1학년때쯤에 진수 체계를 배웠던것으로 기억합니다.
여담이지만, 학교에서는 2진수, 8진수까지만 다뤘던것으로 기억합니다.
우리가 흔히 쓰는 수 체계는 10진수입니다. 진수라는 말은 영어로 base(기초, 기본, 진수)라고 부릅니다.
우리는 10진수의 한자리를 영어로 digit라고 하는데요. 이는 과거에 수량를 셀 때 열개의 손가락을 셌던 것에서
유래한 단어이고, 흔히 10진수를 실생활에서 쓰는 이유 역시 손가락이 열 개이기 때문입니다.
진수체계를 공부할 때 흔히 오해하는 부분이, 진수 체계가 달라지면 수가 달라진다고 잘못 아는 분들이 많은데,
실제로 그렇지 않습니다. 2진수 1111 1111(2) 와 10진수 255(10), 그리고 16진수 FF(16)는 모두 같은 수이죠.
(p.s: 이는 수학에서의 약속이지만, 10진수가 아닌 다른 진수로 수를 표기할 때 몇 진수인지 수 오른쪽 아래에
괄호와 함께 조그맣게 써줍니다. 이 부분은 학교에서도 배우는 부분이므로 자세한 설명은 생략하겠습니다.)
- 10진수 체계 이해하기
10진수의 수 1234 는 아래와 같은 식으로 나타내어질 수 있습니다.
1234 = 1000 * 1 + 100 * 2 + 10 * 3 + 1 * 4
마찬가지로, 임의의 10진수의 수 abcd 는 아래와 같이 나타내어집니다.
abcd = 1000 * a + 100 * b + 10 * c + d
- n진수 체계 이해하기
예를 들어 2진수 11101 은, 10진수의 식으로 나타내면,
2^4 * 1 + 2^3 * 1 + 2^2 * 1 + 2^1 * 0 + 1 * 1 = 29
마찬가지로 n진수의 수 abc 는 아래와 같이 10진수로 고칠 수 있습니다.
n^2 * a + n^1 * b + n^0 * c
( n^0 은 n≠0 일 때 1의 값을 가집니다. )
- 10진수를 n진수로 변환하는 방법
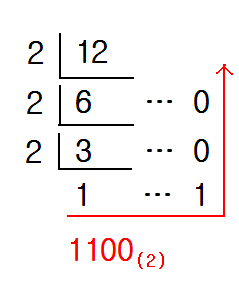
다음은 10진수 12를 2진수로 바꾸는 방법을 그림으로 설명하고 있습니다.
2진수가 아닌 다른 진수로 바꿔야 한다면, 2 대신 해당 진수(base) 값으로 나눠주면 됩니다.
16진수 역시 마찬가지로, 16으로 나누되, 10 이상의 수는 A,B,C,D,E,F 로 표기하면 됩니다.
이를 프로그래밍적으로 표현하면 아래와 같습니다.
|
Public Function ConvertDecimalToBase(ByVal iDecimal As Long, ByVal Base As Long) As String
|
위 함수의 사용법은 다음과 같은 pseudo 코드로 나타낼 수 있습니다.
(pseudo 코드(수도 코드): 거짓(모의; 이해를 돕기 위한) 코드)
(위 함수는 2~16 진수만 바꿀 수 있습니다. Hex$() 함수는 16 진수까지의 수를 취급할 수 있기 때문입니다.)
|
Dim 결과 As String 결과 = ConvertDecimalToBase( 10진수, 진수체계(2~16) )
|
많이 알려지지 않은 사실이지만, 10진수의 소수도 다른 진수로 바꿀 수 있습니다.
소수점을 기준으로, 그 뒤의 숫자는 음수의 제곱꼴로 표현되는 수들로 이루어져 있습니다.
가령, 10진수의 수 123.45 는, 실질적으로
10^2 * 1 + 10^1 * 2 + 10^0 * 3 + 10^(-1) * 4 + 10^(-2) * 5 꼴로 표현이 되고,
|
음수의 제곱은 다음과 같은 꼴로 표현이 됩니다. :p (이를 증명하는 것은 어렵지 않지만, 그냥 필자를 믿으세요. 실제 이 식은 수I에서 배웁니다.)
a^(-b) = 1 / (a^b)
|
위의 규칙에 의해, 10^(-1) 와 10^(-2) 는 실질적으로 1/(10^1), 1/(10^2) 를 나타내므로,
10^(-1) * 4 + 10^(-2) * 5 는 0.45의 값을 가짐을 알 수 있습니다.
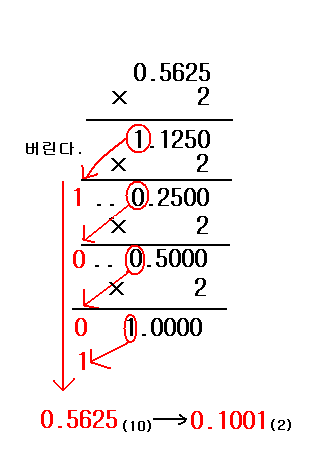
10진수의 소수 0.5625 를 2진수로 고치는 것을 예로 들어서 그림으로 설명하겠습니다.
소수를 고칠 때는 나눗셈이 아니라 곱셈이라는 것과 위에서 아래로 쓴다는 것만이 다를 뿐,
방식은 거의 차이가 없습니다.
소수부가 0이 될때까지 계속 2를 곱합니다. 그리고 정수부의 수를 순서대로 쌓으면 됩니다.
2진수의 수 `0.1001`가 정말 0.5625 일까요? 2^(-1) * 1 + 2^(-4) * 1 즉, 0.5 + 0.0625 = 0.5625
실제로 2진수로 바뀐 것을 볼 수 있습니다. 실제 안쓰일 것 같지만, 컴퓨터에서는 부동 소수점을
표현하기 위해 내부적으로 위와 같은 연산을 수행한 값을 내부적으로 보존합니다.
참고로 Visual Basic에서는 위와 같은 알고리즘을 직접 구현하지 않아도 8진수와 16진수로 쉽게 고칠 수
있게 함수로 구현되어 있습니다.
8진수 = Oct$(10진수)
16진수 = Hex$(10진수)
* 부록: 10진수를 2진수로 고칠 때 조금 더 편리하게 고치는 방법
실제로 손으로 10진수를 2진수로 고칠 때 많이 쓰는 방법으로, 변환할 10진수 밑에 조그맣게 칸을 그립니다.
15 이하의 수라면 4개의 숫자가 들어갈 만한 4개의 칸을 그리는 식으로 먼저 칸을 그립니다. 그 후, 암산으로
대충 합이 맞도록 1과 0을 쓰면 됩니다. 16진수에서 2진수로 고칠 때는 한 자리당 4개의 칸을 그려서 바꾸면 되며,
8진수에서 2진수로 고칠 때는 한 자리당 3개의 칸을 그려서 바꾸면 됩니다.
이와 비슷한 방법으로, 10진수의 수를 2진수로 고칠 때 내부 연산자를 이용해서 빨리 고치는 방법이 있습니다.
물론 이 방법은 10진수에서 2진수로 고칠때만 가능한 이야기입니다.
컴퓨터에서 And 연산자 라는 것이 있는데, A And B 하면 B에서 1인 비트와 A에서 1인 비트를 비교해서 중복된
부분만 1로 비트를 바꾸어 반환하는 연산자입니다. VB에서 And는 논리 연산자도 있는데, 실제론 논리 연산자가
아닙니다. 무슨 말이냐고요? VB에서 True는 -1( 모든 비트가 1인 값 ), 그리고 False는 0( 모든 비트가 0인 값) 으로
통일됩니다. (물론, CBool등의 함수를 쓰면 0이 아닌 값은 모두 True (-1) 로 취급됩니다) 따라서 비트 연산자인 And,Or
등을 써도 논리 연산자처럼 작용할 수 있었던 비밀은 여기에 있습니다.
실제 Code를 통해 보여드리겠습니다.
|
Public Function ConvertDecimalToBinary(ByVal iDecimal As Long) As String
|
이 글을 읽으시는 독자중 Log() 함수가 뭔지 모르시는 분들이 있을 것 입니다.
이 Log() 함수는 수I 과정에서 배우는 함수 중 하나로, 밑을 10으로 하는 log(자연로그)를 말합니다.
a^x = b에서 x는 log함수를 이용해서 나타내면 log_a(b) (밑이 a인 log(b)) 로 구할 수 있습니다.
Log(X) / Log(N)은 밑 변환 공식을 이용한 것인데요. 복잡한 설명 없이 간략하게 알맹이만 설명하자면,
자리수 = Fix(Log(수치) / Log(진수체계)) + 1
와 같이 자리수를 구할 수 있습니다. 자세한 증명과 유도 과정 등은 수I (고2) 에서 배우세요.
강좌를 이만 줄이겠습니다.
읽어주셔서 감사합니다.