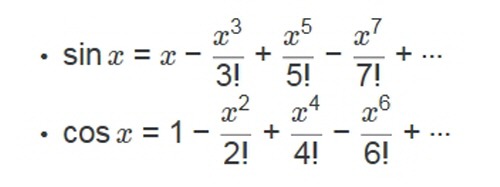삼각함수(三角函數)
수학에서 사용하는 각에 대한 함수이다. 직각 삼각형의 한 예각 ∠A\angle A∠A의 크기에 의하여 결정되는 삼각비를 ∠A\angle A∠A의 함수로 보고 정의한 함수 및 이것과 대수함수 등과의 합성에 의해서 얻어지는 여러 함수를 말한다. 대표적인 초월함수이다.
인도에서 처음 탄생하였다. 그 후 이슬람에서 이를 발전시켰고 이것이 유럽으로 건너갔다. 사인(sine)은 원래 인도 천문학에서 나온 개념으로, 산스크리트어 ज्या(jyā, 활시위)를 음차한 아랍어 jiba의 번역어이다. 12세기 이탈리아의 수학자 크레모나의 게라르도가 jb라고 약칭된 것을 جيب(jayb, 주머니, 가슴)로 착각하여 라틴어 sinus(빈 공간, 옷주름, 가슴)로 번역하게 된 것이 어원이다. 그리고 코사인은 sine의 complementary라는 뜻에서 cosine이 되었다(그래서 sin(π2−θ)=cosθ \sin ({\pi \over 2} - \theta) = \cos \theta sin(π/2−θ)=cosθ 이다). tangent는 접한다(touching)는 뜻의 라틴어에서 유래하였다. (많이 사용되지는 않지만) 한자로는 사인을 정현(正弦), 코사인을 여현(餘弦), 탄젠트를 정접(正接), 시컨트는 정할(正割), 코시컨트를 여할(餘割), 코탄젠트를 여접(餘接)이라 한다.
자매품으로 쌍곡함수(hyperbolic function)를 배우는데, 삼각함수가 원과 연관된다면 쌍곡 삼각함수는 쌍곡선과 연관되고, 둘 다 미분방정식, 함수 이론에서 쓰인다는 점도 비슷하고, 여러 가지 공식이나 성질도 비슷하다. 그리고 복소수를 배우면 더 연관된다. 특수 상대론에서 사용되는 기하학에서 쌍곡함수의 위상은 평범한 기하학에서 삼각함수의 위상과 비슷하다.
당신이 대학에 진학해서 수학을 계속 본다면 삼각함수를 애인처럼 옆구리에 끼고 살 확률이 은근히 높다. 쉬운 예를 하나 들면 물결 모양의 곡선을 얻기 위해서는 삼각함수가 꼭 필요하다.
원래는 고등학교 1학년 과정에 삼각함수가 들어있었으나 그것이 2009 개정교육 과정 개편으로 사인 법칙과 코사인 법칙이 빠진 상태로 이과용 과목인 미적분Ⅱ으로 넘어가 문과 수학에서 빠지고 말았다. 따라서 2014년 이후에 고등학교로 입학한 문과생들은 아예 삼각함수를 배우지 않게 되었다. 그러나 2015 개정 교육과정에서 삼각함수가 지수함수, 로그 함수와 함께 수학Ⅰ에 포함되어 사실상 부활 예정. 이 때 사인 법칙과 코사인 법칙이 함께 부활한다. 다만, 이과 기준으로는 줄었다. 삼각함수의 합성이 개편안엔 빠진다는 예고가 없었는데 은근 슬쩍 빼버렸다.
일본에서는 삼각비를 수학 I, 삼각함수를 수학 II에서 배운다.
삼각비
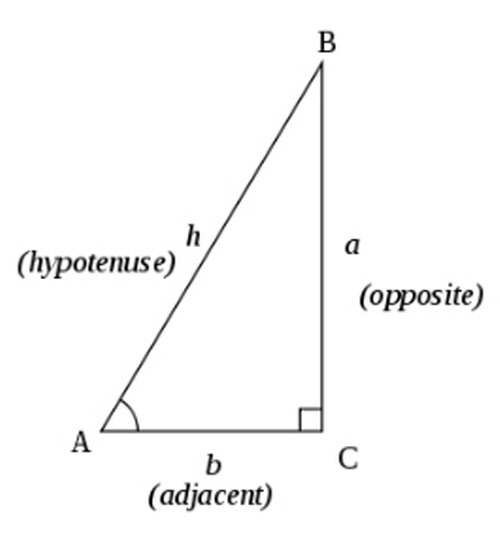
중학교 수학 교육과정에서 정의하는 방법으로, 직각삼각형을 이용한 정의라고 한다. 다만, 직각삼각형의 특성상 정의역이 0 < A < π/2rad 로 제한되기 때문에, 정의역을 모든 실수로 정의하지 못한다는 단점이 있다. 따라서 둔각에 대한 삼각함수의 정의가 이상하게 보일 수 있다(한 각이 둔각인 직각 삼각형은 존재하지 않으므로).
직각삼각형에 대해 sine, cosine, tangent를 다음과 같이 정의한다.
• sinA=a/h
• cosA=b/h
• tanA=a/b
영미권 학생들은 sin cos tan을 각각 SOH CAH TOA, sine = opposite over hypotenuse, cosine = adjacent over hypotenuse, tangent = opposite over adjacent 이렇게 외운다. 한국어의 OO 분의 XX와 영어의 XX over OO 어순이 달라서 그렇다.
그리고 이 함수들의 역수로서 cosecant, secant, cotangent 함수를 다음과 같이 정의한다.
• cscA=1/sinA=h/a
• secA=1/cosA=h/b
• cotA=1/tanA=b/a
단위원을 이용한 정의
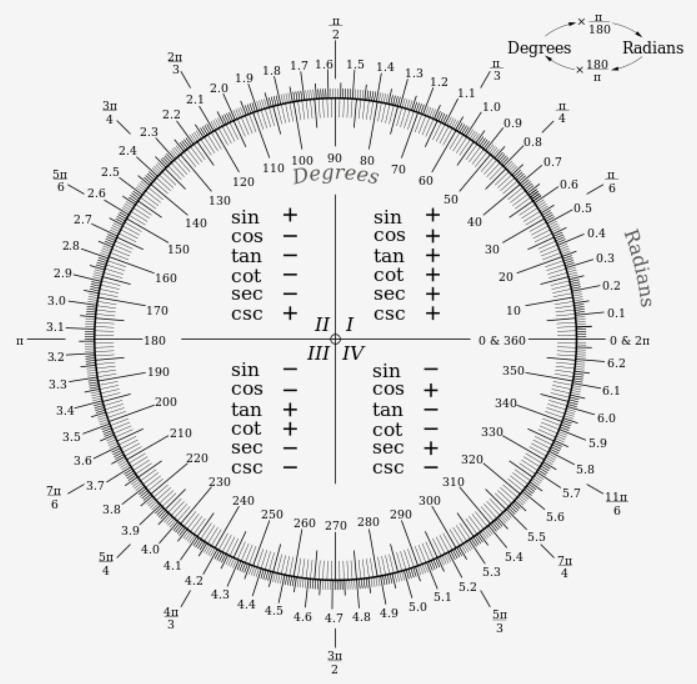
2009 개정 교육과정 고등학교 미적분Ⅱ 과정에서 정의하는 방법으로, 평면에 OOO를 원점으로 하는 좌표평면에 대해 이 평면 위의 점의 좌표를 (x,y)로 표시하고, x-축의 양의 방향에 대하여 각 θ를 만드는 사선 OP를 그어 O를 중심으로 하는 단위원과의 P교점을 P라 하면 x좌표를 cosθ, y좌표를 sinθ, OP의 기울기를 tanθ로 정의한다.
흔히 말하는 얼싸탄코가 단위원 정의에서 생각해보면 당연한 것이다. 단위원에서 x좌표가 양수인 부분이 1,4사분면, y좌표가 양수인 부분이 1,2사분면, 기울기가 양수가 되려면 1,3사분면을 지나야 한다.
위와 같이 정의하고 tangent와 기타 함수들은 다른 정의와 마찬가지로 정의한다. x에 아무런 수를 넣어도 위의 무한합이 무한대로 발산하지 않는다는 것이 보장되어야 위의 정의가 유효할 텐데, 그 사실은 이미 수학적으로 보장되어 있으니까 마음껏 쓰면 된다.
이 무한합이 발산하는가 아닌가는 비율판정법을 사용해서 증명하는게 가장 편한데, 다음과 같다.
어떤 실수 x값을 대입하더라도 반드시 수렴한다. 또한 이 수열합의 수열은 절대수렴하는 수열이기 때문에 복소수를 대입하더라도 마찬가지 정의에 의하여 절대수렴함이 확인되어 있다.
복소평면을 이용한 정의
주기
실함수 fff에 대하여 적당한 상수 k≠0을 잡을 때, fff의 정의역에 속하는 임의의 x에 대하여 f(x+k)=f(x)가 성립하면, f를 주기함수라 하고, k를 f의 주기라 한다. 양인 최소주기는 기본주기라고 한다. 삼각함수는 모두 주기함수이며, tanθ, cotθ를 제외하면 기본주기는 2π이다. tanθ, cotθ의 기본주기는 π이다.
극좌표
수직으로 보기 좋게 떨어지는 직교좌표를 굳이 극좌표나 구좌표 같은 또다른 좌표계로 바꾸는 이유는 회전 운동이나 모든 방향으로 대칭적인 움직임/변화 등을 기술할 때 직교좌표를 쓰면 조금만 복잡해져도 기술하기가 어렵기 때문이다. 예를 든다면 지구 표면 근처에서의 위치를 직교좌표 3개로 쓰는 것보다는 위도, 경도, 고도로 표현하는 것이 편리하다는 것이 있다.
거듭제곱
삼각함수는 일반적인 함수와는 달리, 지수가 동일함수 합성이 아닌, 결과값의 거듭제곱으로 쓰이므로 주의해야 한다.
삼각함수의 여러 공식
미분
삼각함수 미분의 육각형
이 육각형을 사용하려면 먼저 미분하려는 함수가 속해 있는 +,- 부호를 확인한다. 그리고 미분하려는 함수에서 시작하는 화살표로 가는 함수를 모두 곱한다. (이때 이중선은 제곱하라는 뜻이다.) 이 과정을 그림으로 예를 들어 보이면 다음과 같다.
적분
교과서에서는 삼각함수의 부정적분을 위 미분 공식을 거꾸로 한 형태만 가르친다. 즉, 사인과 코사인의 적분을 제외하고는 교과서에서는 찾아볼 수 없는 공식들이다. 하지만 나머지 네 개 모두 치환적분을 이용하여 쉽게 증명할 수 있으니 미적분 II를 공부한다면 한 번 해보자.
다양한 적분 공식
기본적인 여섯 개의 삼각함수 적분법은 위와 같지만, 적분에서는 미분에서의 Chain Rule과 같은 정리가 존재하지 않기 때문에, 삼각함수를 적분하는 수많은 공식이 존재한다.
사인함수와 코사인함수를 거듭제곱한 꼴의(자연수 한정) 식을 0부터 π/2 까지 정적분하는 공식. 계산량을 상당히 줄여준다. 학생들에게 도움이 될.. 지도? 이 식은 초구의 초부피를 초구면 좌표계 형식으로 구하는 방법에도 효과적으로 쓰인다
역삼각함수
참고로 수학자마다 표기가 제각각이다. 아크사인만 해도 asin(MATLAB 문법에서 사용), arcsin(가장 정확한 표기법), sin-1(수학계에서 그다지 권장하지 않는 표기법) 등의 표기가 난립하고 있다.
한국에서는 고등학교에서 아예 다루지 않으나, 계산기를 사용하는 해외에서는 보통 중학교 3학년 정도에 배운다. 화학에서 용어는 사용하지 않으면서 언급하기도 한다. 메테인의 결합각 약 109.5도가 사실은 arccos(-1/3)이다. 이 각도가 나오는 것은 벡터의 내적으로 증명할 수 있다.
일반적인 삼각함수는 오일러의 공식을 이용해서 복소평면상에서 정의할 수 있고, 이렇게 확장하면 역함수를 정의하기가 용이하다.
쌍곡선 함수
역쌍곡선함수
쌍곡선함수는 삼각함수는 아니고 지수함수로 만들어진 함수이다. 하지만 삼각함수와 상당히 유사한 성질을 지닌다.
쌍곡선함수 미분의 육각형도 위 항목의 삼각함수 미분의 육각형과 매우 흡사하다. 유일한 차이점은 삼각함수 미분의 육각형에서 +,- 경계선이 시계방향으로 60도 기울었다는 점이다.
생각보다 고등학교 교육과정에서 많이 묻는 함수이다. 미적분2, 기하와 벡터에서 자주 볼 수 있다. 다만 cosh 와 sinh 같은 직접적 표기가 교과서에 나오지는 않는다.
야코비 타원함수
왜 이렇게까지 하냐면 타원에 관한 함수는 대부분 부정적분을 찾을 수가 없기 때문이다. 특히 타원의 정확한 둘레를 일반적인 함수로 표현하는 것이 불가능하기 때문에 여러가지 타원용 함수를 만들어 따로 표기하는 것.
복소함수에서의 삼각함수의 절댓값
삼각방정식과 부등식
삼각함수의 그래프를 이용하여 정해진 값에 해당되는 미지수의 값을 구하면 된다. 사인과 코사인이 같이 주어지는 경우 공식을 이용해 한 종류의 삼각함수로 고쳐야 하는데 그게 상당히 복잡하다.