이산적 퓨리에 변환
(-Fourier- , 離散的-)
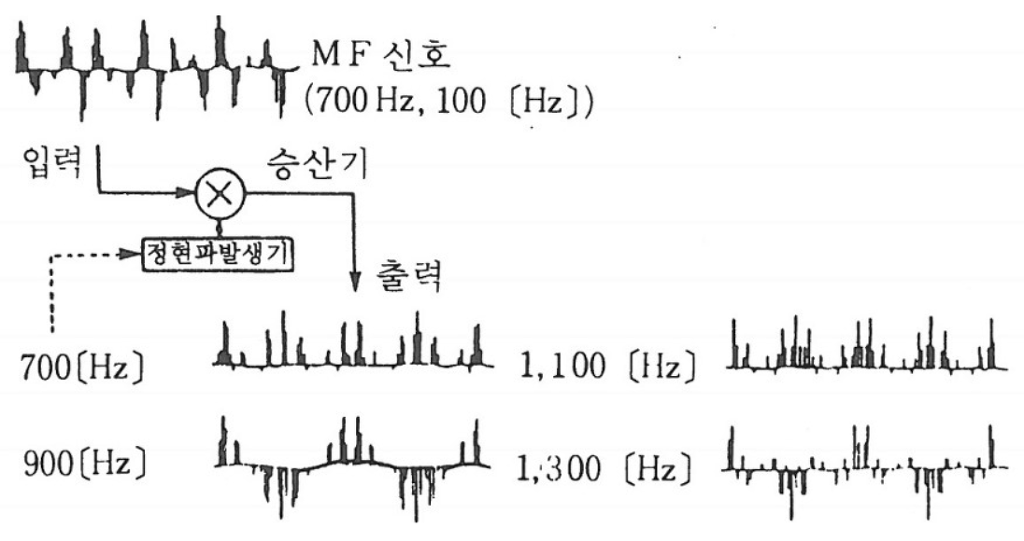
아날로그 신호처리를 하여 입력 신호중에 어떠한 주파수 성분의 정현파가 포함되어 있는가를 조사하는 기법으로서 푸리에 변환이 사용된다. 표본화된 이산적 신호로부터 표본화전(前)의 아날로그 신호에 포함된 각 주파수 성분을 구하는 기법이 이산적 푸리에 변환(DFT : Discrete Fourier Transform)이다. 그림은 이산적 푸리에 변환의 원리를 나타낸 것이다.
이산적 푸리에 변환의 원리
이 그림에는 입력신호로서 MF 신호(700㎐+1, 100㎐)를 예로 한 것인데 입력신호에 여러가지 주파수의 정현파를 교합(交合)한 경우의 출력신호의 변화를 나타낸다. 700㎐ 및 1,100㎐의 정현파를 승산(乘算) 한 경우에 출력신호의 파형은 정(+)측(側)으로 치우치게 되고, 기타의 경우에는 음양(-, +)양측으로 분산된다. 일반적으로 치우침의 정도를 정량적으로 파악하기 위해서는 출력신호의 값을 1주기분(周期分) 가산하는 것이 좋다.
교합시킨 주파수와 같은 주파수성분이 입력신호에 포함되어 있으면 가산결과는 유한치(有限値), 포함되어 있지 않으면 가산결과는 0이 되고 그 값이 포함된 주파수성분의 크기에 비례한다는 것이 수학적으로 증명되어 있다. 이산적 푸리에 변환에는 이와 같이 정현파의 승산(乘算) 및 승산 후 출력의 가산을 하여 각 주파수성분을 구한다.
퓨리에(Fourier) - 통신공학이 아니더라도 교류(또는 광의의 개념인 파동)를 해석하는데 있어 퓨리에는 반드시 넘어야 할 산이 된다. 여기에 오일러 공식이 부가되어 공식들이 요동을 치면 배멀미로 생고생하는 경지에 이르고야 만다.
전기전자에서 직류(DC)는 비교적 교류(AC)에 비해서 쉽다. 교류는 사간에 따라 신호가 변화하는 성질을 가지고 있기 때문에 분석하는 것이 용이하지 않다. 정작 정현적인 교류도 어려운데, 여기에 도무지 종잡을 수 없는 신호가 떡하니 출현하게 되면 보통사람의 머리로는 분석하기가 하늘의 별따기 정도로 되어 버린다. 하지만 신호가 개차반 같더라도 주기적이라면 직류와 정현파(Sine), 여현파(Cosine)가 합성된 파형이라는 논리가 생긴다. 여기서 퓨리에 급수(Fourier Series)가 시작된다.
(Jean Baptiste Joseph Fourier, Baron de, 1768~1830)
급수(級數)라는 것은 무한급수에서 볼 수 있듯이, 수들의 계속적인 더하기가 무한대로 이어진 것을 의미하듯이, 더하기로 계속 이어진 수를 말한다. 따라서 퓨리에 급수(Fourier Series)도 무언가 계속 더해진 형태를 갖는다는 것을 짐작할 수가 있다.
복잡한 파형은 기본파의 정수배가 합해진 것을 쪼갤 수 있다는 것이다. 만약 복잡한 파형의 기본 주파수가 1Hz 라면 복잡한 파형은 이 기본 주파수에 ×1, ×2, ×3... 이라는 정수배의 주파수인 2Hz, 3Hz, 4Hz.... 가 더해(합성)졌다. 그래서 퓨리에 급수를 보면 사인파든 코사인파든 기본주파수의 정수배가 곱해진 형태가 눈에 보인다.
정수배란 ×1, ×2, ×3, ×4, ×5, ×6...로 기본주파수에 곱해진 주파수 소숫점이 있는 배수가 아닌 주파수를 의미한다. 결론적으로 퓨리에 급수는 세상에 존재할 수 있는 모든 파동을 수식으로 나타낸 것에 불과 한데 사인과 코사인의 조합으로 만들어진다.
EQ(Equalizer)와 퓨리에변환
보통 EQ라고 줄여서 이야기하는 이퀄라이저(Equalizer)는 등화회로(等化回路)를 내장한 오디오기기라고 정의할 수 있다. 평탄한 어떤 소스음을 100% 그대로 증폭하고 출력할 수 있다면 EQ는 필요하지 않다. 그런데 소스기기에 있어서 고음을 높혀 녹음하던(LP, Tape 등) 저음을 높혀 녹음하든 본래의 음과 다른 음이 들린다면 원래대로 복귀시킬 방법이 필요하고 그때 사용되는 회로를 EQ. 회로라고 한다. 내장 EQ를 밖으로 꺼내 사용자가 그래픽컬하게 주파수들을 조정할 수 있도록 만들어 놓은 것이 독립기기로서의 이퀄라이저이다. 예를 들어, 예전에는 Cassette Tape를 많이 사용했는데 보급형 데크의 경우는 넓은 음역을 내는데 이퀄라이저 장비를 이용했다.
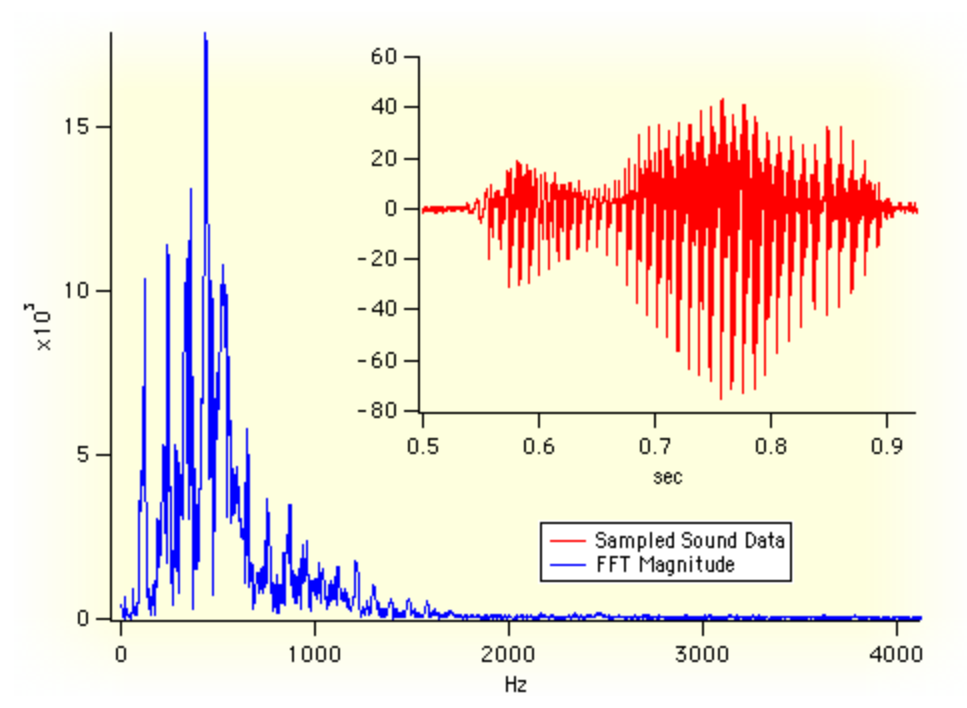
이는 각 주파수구간별로 Band Pass Filter를 사용하여 주파수별 선택도 다시말해 선택주파수 이외의 구간에 대해서는 감쇄될 수 있도록 하고 감쇄된 만큼 또는 미리 감쇄될 만큼 증폭하여 손실분을 보완하는 방법이 있다. 스펙트럼이 시각적으로 출력되는 EQ의 경우는 마이크로컨트롤러를 배치하고 퓨리에변환(Fourier Transform)을 이용하면 입력신호 복합음에서 개별 주파수별 Peak를 구할 수 있고 그것을 레벨값으로 쉽게 표현할 수 있다. 그렇게 하면 보기도 좋은 스펙트럼-에널라이저가 만들어 진다.