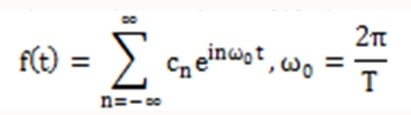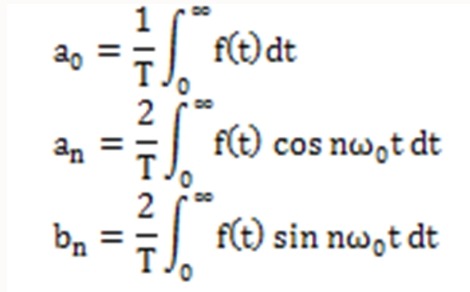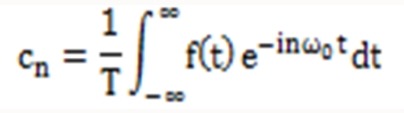푸리에급수의 함수적 정의에 대해 알아보자

[관운]

푸리에급수의 함수적 정의

푸리에 해석은 과학적, 기술적 문제 해결에 있어서 필수 불가결한 도구의 하나이다.

1.푸리에 급수(Fourier Series)

프랑스의 수학자 푸리에(J.Fourier)는 임의의 주기 T를 갖는 주기 함수(Periodic Function) f(t)는 다음과 같이 삼각함수 (Trigonometric Function)의 급수로 전개할 수 있음을 알아냈다.

이 식을 푸리에 급수 또는 실(수) 푸리에 급수 (Real Fourier Series) 라고 한다.

모든 주기 함수를 삼각함수의 급수로 나타낼 수 있다는 것은 푸리에의 놀라운 발견이었다. 왜 이것이 가능한 것일까? 그 비밀은, 여기에 선택된 함수들 간의 관계에 있다.

이들은 모두 서로 직교(Orthogonal)하는 함수들이다. 벡터에 대해 내적(Inner Product)이라는 연산이 있듯이, 함수에 대해서도 내적을 정의할 수 있는데, 두 함수 f(t)와 g(t)의 내적은 다음과 같다.

이와같이 함수의 내적을 정의했을 때, 그 내적이 "0"이 되면 두 함수는 서로 직교한다고 한다.

다시 푸리에 급수로 돌아가 보면, 좌변은 원함수 f(t) 이고, 우변은 서로 직교하는 삼각함수들("1"이라는 상수 함수 포함)의 일차결합(Linear Combination)이다. 이것은 마치 벡터공간에서 임의의 벡터가 기저벡터(Basis Vector)들의 일차 결합으로 표시될 수 있는 것과 같다. 따라서, 이 때 우변의 함수들을 기저 함수 (Basis Function)라고 한다. 또한 벡터 공간에서 기저 벡터가 정해지면, 그 후로는 기저 벡터는 생략하고, 기저 벡터의 계수로 구성된 좌표만으로 벡터를 표현하듯이, 푸리에 급수에서도 기저 함수가 정해지면, 푸리에 계수(Fourier Coefficient)만 가지고 함수를 나타낼 수 있다.

그런데, 여기서 한가지 짚고 넘어 갈 부분은 기저 함수에 대한 것이다. 즉, 직교하는 함수들은 삼각함수 말고도 많이 있고 그것들을 사용해서도 푸리에 급수와 같은 전개가 가능하다는 것이다. 그러나 가능은 하지만, 유용하지는 않다. 삼각함수를 기저 함수로 사용했을 때, 가능할 뿐만 아니라 유용한 이유는, 삼각함수의 독특한 성질 때문이다. 삼각함수는 미분과 적분을 몇번이고 해도 그 함수의 형태(파형)이 변하지 않는 유일한 함수이다. 지수함수(Exponential Function)도 이와 같은 성질이 있는데, 사실상 지수 함수를 복소 지수 함수 (Complex Exponential Function)로 확장하면 삼각 함수는 그 안에 포함이 되므로 이 둘은 같은 함수라고 할 수 있다. 따라서, 푸리에 급수는 기저 함수를 복소 지수 함수로 바꾸어 다음과 같이 쓸 수도 있다.

이 식을 복소 푸리에 급수(Complex Foureier Series)라고 한다, 푸리에 급수와 복소 푸리에 급수 식의 차이를 살펴보면, 기저 함수가 삼각함수(실함수)에서 복소지수함수(복소함수)로 바뀐것과, 합계를 구하는 구간이 [0,무한대]에서 [-무한대, 무한대]로 바뀌었음을 알 수 있다.

합계구간이 바뀐 것은, 전자에서 삼각함수는 코사인 함수와 사인 함수 두 가지에 대해 [0,무한대]구간에 대해 합을 구하는것에 대응하여, 후자에서는 복소 지수 함수 한 가지에 대해 합을 구하는 대신, 구간이 두배로 늘어나서 [-무한대, 무한대]으로 된 것이다. 계수도 전자는 실수계수를 갖고, 후자는 복소수계수를 갖는 것도 둘 간의 차이이다. 그러나 이러한 차이들은 형식적 차이이며, 결국 둘은 같은 내용의 다른 표현이라고 할 수 있다.

실 푸리에 급수의 계수는 다음과 같이 얻어진다.

또한 복소 푸리에 급수의 계수는 다음과 같이 얻어진다.

내적의 정의에 따라, 복소공액함수를 곱하므로 exp(inw0t)가 아닌 exp(-inw0t)를 곱함을 유의하자.

[김인선]

제가 글을 옳려 놓고서도 이것이 무엇을 의미하는지 전혀 알지 못합니다. 하지만 신호의 변환에 있어서 규칙적인 이론이 존재하고 있다는 사실을 간과할 수는 없습니다. 그나마 푸리에 이론은 카오스 이론에 비해 좀 낫다고 하겠습니다. 좀더 쉽게 설명하자면 인간이 편리에 의해 만들어진 것들이 잘못되어졌다고 느껴 졌을때 되돌아가는 것 또는 신호의 변조와 복조 사이에 퓨리에 이론과 카오스 이론이 상충되어졌을 때 더많은 수학적 연산이 필요하다는 것을 알았습니다.