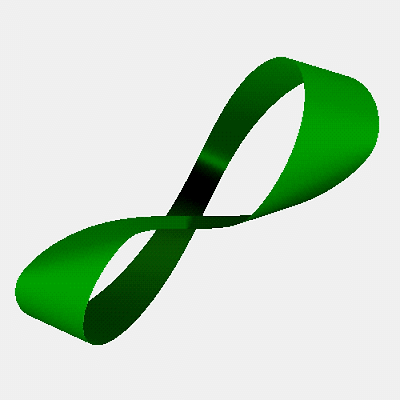뫼비우스의 띠
뫼비우스의 띠는 모든 것에 안과 밖의 구별이 있다는 고정 관념을 깨게 하였다.
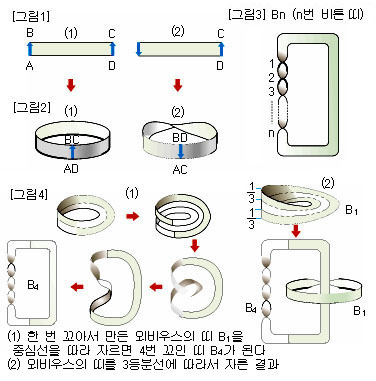
직사각형 모양의 띠의 양끝을 그대로 붙이면 보통의 띠가 된다. 직사각형 모양의 띠의 끝을 한 번 꼬아서 즉, 180도 회전시켜서 다른 쪽 끝에 붙이면 색다른 모양의 띠가 만들어진다.
뫼비우스의 띠는 이와 같이 긴 테이프를 한 번 꼬아서 양끝을 붙여서 만든 곡면이다. 꼬지 않고 그냥 붙인 테이프와 뫼비우스의 띠는 전혀 다른 곡면이며 특히 위상수학에서 좋은 예가 되고 있다.
보통 테이프는 경계가 두 개인 반면 뫼비우스의 띠는 경계가 하나밖에 없다.
즉, 보통 테이프는 한 쪽 면은 노란색을, 다른 쪽 면은 빨간색을 칠할 수 있으나 뫼비우스의 띠는 면을 따라 색칠하다 보면 모두 한 가지 색으로 칠해짐을 알 수 있다.
이러한 독특한 성질이 있는 띠를, 1865년 처음 발견한 독일의 수학자의 이름을 따서 '뫼비우스의 띠'라고 한다.
뫼비우스의 띠처럼 만들어진 2차원 공간에서 여행을 하여 한 바퀴 돌아 처음 자리에 오면 처음 모습과는 좌우가 바뀐다. 즉, 이런 공간에서는 좌우의 바향은 아무 의미가 없게 되는 것이다.
공장에서 기계를 돌리는 벨트를 뫼비우스의 띠처럼 만들어서 쓰기도 한다. 두 개의 바퀴에 둥그런 띠 모양의 벨트를 그대로 걸면 기계의 한쪽 면만 닳게 되는데, 이것을 뫼비우스의 띠처럼 한 번 꼬아서 걸게 되면 벨트의 양쪽 면이 골고루 닳아 벨트의 수명이 훨씬 길어진다. 또 그대로 걸면 쉽게 빠지던 벨트도 이렇게 걸면 잘 빠지지 않는다.
4차원 항아리-클라인병(Klein's bottle)
1. 설명
클라인병(甁) ·클라인면(面) ·클라인관(管)이라고도 한다. 독일의 수학자 F.클라인이 고안하였다. 이 항아리에서는 항아리의 양끝이 접속되어 있다는 점에서는 분명히 닫혀 있는 데도 사실은 열려 있다. 이 항아리의 용도는 아직 발견되지 않고 있는데, 이유는 액체를 넣으면 흘러나가기 때문이다. 그러나 뫼비우스의 띠는 기계 벨트용 등으로 이미 실용화되었다. 뫼비우스의 띠 외에도 면이 하나밖에 없는 도형이 있다. 가장자리가 없어 '내부와 외부가 구분되지 않는 입체'는 이것을 고안한 독일의 수학자 클라인의 이름을 따서 '클라인 병'이라고 한다.두 개의 뫼비우스의 띠를 경계를 붙이면 클라인 병이 만들어진다.즉, 직사각형은 2차원 도형이지만 한 번 꼬아서 만든 뫼비우스의 띠는 3차원의 도형이다. 이와 마찬가지로 클라인 병은 밑면과 윗면이 뚫려 있는 원기둥으로 만든다. 옆면을 뚫고 들어가서 밑면에 윗면을 붙이면 클라인 병이 되는데, 4차원에서는 옆면을 뚫지 않고도 두 변을 붙일 수 있다.클라인 병은 3차원 공간에서 표현할 수 있는 도형이 아니고 4차원 공간에 있어야 자연스러운 도형이다.클라인 병은 가장자리가 없고 면이 하나밖에 없는 곡면이고 뫼비우스의 띠는 가장자리가 있는 면이 하나밖에 없는 곡면이다. 클라인 병에는 경계가 없고 방향도 없기 때문에 클라인 병에 물을 부으면 붓는 것과 동시에 물이 줄줄 흐르게 된다.
2. 만드는 방법
이 항아리를 만들 때는 우선 직사각형 ABCD(얇은 고무판과 같은 것으로 상상한다)의 A와 B, C와 D를 겹치고 AD, BC를 맞붙여서 원관(圓管)을 만든다. 이렇게 만든 원관을 한 번 틀어서 A와 C, B와 D를 겹쳐 AB, CD를 붙인 다음, 원관의 곡면에 구멍을 뚫고 집어 넣어 양끝(입구)을 접속시키면 된다. 이것은 3차원 유클리드공간 내에서는 실현될 수 없다.
3. 클라인의 유리병과 상대성 이론
상대성 원리란 일단 상대적이라는 데서 출발합니다. 버스를 타고 출발하면 정류장이 움직이는 것 처럼 보입니다. 정류장에 서 있는 사람이 보면 버스가 출발하는 것으로 보이지요. 간단한 상대성의 원리입니다.이는 누구나 아는 것입니다. 그러나 아무것도 없는 우주의 한 복판에서 우주선에 타고 있는 데 맞은편 우주선이 움직인다고 상상하면 어느 것이 움직이는지 알 수 있을까요. 알 수 없습니다. 기준점이 없기 때문이지요. 이상은 우리가 관찰하는 것이 과학적으로 볼 때 상식적인 것과 다름을 알 수 있습니다. 시간과 공간이 예전에는 이와 같은 것으로 생각했지요. 지구의 1분과 우주의 어느 곳의 1분은 항상 같다고 생각했습니다. 그러나 아인슈타인은 그렇지 않다는 것을 머리로 생각했습니다.
아인슈타인이 생각한 것은 어떤 것일까요?좀 수수께기 같지만 잘 생각해보세요..여기 우주선이 지구를 출발하여 멀어지면서 6분에 한번씩 지구에 빛(신호)을 보낸다(쏜다)고 합시다. 지구가 가만히 있으면 6분에 한번씩 신호를 받겠지요. 그런데 지구가 우주선에서 매우 빠른 속도로 멀어진다면 6분에 한번씩 지구로 보내는 신호를 지구에서는 6분보다 더 늦게 그러니까 예를 들면 12분에 한번씩 받게 될 수도 있는 것입니다. 반대로 지구가 우주선에 매우 빠른 속도로 가까이 다가 간다면 6분에 한번씩 지구로 보내는 신호를 도리어 3분에 한번씩 받게 될 수 있습니다. 우주선에 있는 사람과 지구에서 신호를 받는 사람의 경우를 보면 우주선에서 6분이라는 시간간격이 지구에서는 12분 또는 3분 간격으로 각각 다르게 관찰되는 것입니다. 여기서 시간여행이 나옵니다. 만일 지구가 매우 빠르게 우주선의 반대방향으로 이동하다가 다시 우주선의 방향으로 더 빠르게 움직일 경우 되돌아온 우주선에 탄 사람과 지구에 있는 사람은 서로 다른 시간이 지났음을 경험하게 됩니다.즉 지구에 있는 사람이 더 젊고 우주선을 탄 사람이 더 늙겠지요.
이러한 원인은 무엇일까요? 이는 신호 즉 빛의 속도는 초당 30만 킬로미터로 일정하기 때문입니다. 빛의 속도가 일정하기 때문에 빛과 같은 속도로 멀어질 경우 멀어지는 만큼 걸리는 시간이 늘어지고 이에 따라 시간이 다르게 가는 것입니다. 다른 예를 들어볼까요.. 여러분이 지금 지구 위에 서있고 정확히 30만 킬로미터 떨어진 곳에 여러분 친구가 빛을 보내면 1초후에 빛을 받을 수 있습니다.
그러나 여러분의 친구가 빛의 속도로 움직이면서 신호를 보낸다면 두번째 신호부터는 1초보다 늦게 여러분이 신호를 받게 됩니다. 여러분의 친구가 1초에 한번 간격으로 빛을 보내지만 빛이 오는 거리가 길어지면서 여러분들은 1초보다 느린 간격으로 신호를 받게 되지요. 이것이 뜻하는 것은 무엇일까요. 여러분의 친구의 1초와 여러분의 1초가 같지 않은 것이지요. 즉 관찰하는 사람의 운동에 따라 시간과 공간의 측정은 달라지는 것입니다. 우리가 하늘을 바라볼 때 빛의 거리로 1만광년(광년은 빛이 1년간 가는 어마어마한 거리임)에 떨어진 곳의 별빛(내가 보는)은 1만년 전에 그 별을 출발한 빛입니다. 그러면 1억광년 쯤 떨어진 곳에 있는 별은 내가 지금 보는 순간에 이미 사라져 버렸을 수 도 있지요.상식적으로 생각하면 이미 존재하지 않는 별이 우리에게는 존재하는 것으로 보이는 것이지요. 즉 옛날 사람들이 생각하는 것처럼 시간과 공간은 절대적인 것이 아니라 관찰자의 위치에 따라 상대적인 것이 되는 것입니다.
4. 클라인의 유리병 이미지
클라인병은 4차원상에서 자연스런운 물체이다. 3차원 공간에서 풍선은 풍선의 내부와 외부라는 두개의 공간이 존재한다. 놀이공원에서 볼 수 있는 수소풍선은 내부공간에는 수고가스가 채워져있는 모양이다. 이렇게 3차원 공간에서입체의 특징은 닫힌 공간이 존재하거나 아니면 닫혀있지 않은면 반드시 모서리가 존재한다. 종이를 말아서 윗면과 밑병이 없는 원기둥은 면과 면이 넘어가는 모서리가 존재한다. 클라인 병은 이런 기본적인 3차원 공간의 조건을 만족하지 못한다. 아래 그림에서 보듯이 내외부가 모두 한 공간에 연결되어있다. 즉 입구에 물을 부으면 입구로 물이 흘러나온다. 이것이 의미하는 것은 닫힌 공간이 존재하지 않는 것임을 의미한다. 즉, 입구와 출구가 하나인 입체가 되는 것이다.
클라인병 구조로 되어있는 동굴이 있다면 이 탐험자는동굴 내부를 모두 탐험하고 자기가 처음에 들어간 입구로 나오게 될 것이다. 즉 다른 공간으로 넘어가지 못할 것이다. 영화매트릭스에서 키아누리부스가 지하철역에 갇힌 것도 4차원공간에서는 얼마든지 가능한 일이다. 즉 아무리 빠져나갈려해도 결국은 그 자리로 돌아올 수밖에 없는 것이다.
차원에 관한 이야기를 잠깐 해보려고한다. 일차원은 직선을 의미한다. 직선상의 모든 점은 거리가 존재한다. 직선상에 임의 점을 A, B, C를 놓아보자.. 그러면 반드 가장 먼 두 점이 존재할 것이다. 2차원(평면)이나 3차원(공간)에서는 선을 구부릴 수 있으므로 가장 먼 두 점을 붙일 수 있을 것이다. 이것이 의미하는 것은 일차원에서 먼 두 점이 다음 차원에서 공존할 수 도 있음을 의미한다. 서울과 뉴욕은 공간상에서 공간적 거리가 존재한다. 하지만 4차원공간에서는 공간을 구부려서 두 도시 일치할 수 있다. 얼마든지..이 것은.,,여기가 서울일수도 있고 뉴욕일 수도 있다는 것이다. 같은 시공(같은 사건의 지평선)이다. 3차원의 모든 지역은 4차원에서 하나이다. 즉, 저차원에서 불가능한일 고차원에서 얼마든지 가능함을 알 수 있다.
다른 예를어본다면 풍선이 있다. 풍선 내부에 동전이 들어있다고 하자. 풍선을 터트리지 않고 동전을 빼내는 일은 3차원에서 불가능하다. 그러나 4차원에서는 얼마든지 가능하다. 풍선을 터트리지 않고 연필이 얼마든디 통과할 수 있다는 것이다. 클라인병의 경우도 마찬가지로 동전을 꺼내 올 수 있다. 영화속에서 자주 등장하는 단골 소재이다. 즉 문을 열지 않고 벽을 통과하는 방법은 4차원에서 무수히 많이 존재할 수 있다는 것을 알 수 있다.
