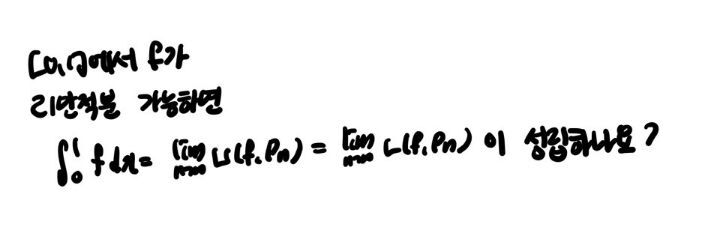
일반적으로 저 사진이 가능한가요? 아니면 Pn이 균등분할일때만 성립하나요?
다음검색
댓글
댓글 리스트-
답댓글 작성자김성희 작성시간 21.02.06 mathshin 네, n을 빼고 ||P||를 충분히 작게 잡아주는 형태로 가면 될 것 같아요. 그리고 적분값은 lim 계산이 아니라 inf{U(f, P)}로 하고요. 소구간에서 함수의 sup은 항상 1이니까요.
-
답댓글 작성자mathshin 작성자 본인 여부 작성자 작성시간 21.02.06 김성희 n을 빼고 ||P||를 충분히 작게 잡아주는 형태가 어떤건가요?
-
답댓글 작성자김성희 작성시간 21.02.06 mathshin 아;; 적분가능을 보일 때엔 P 하나만 선택해주면 되는군요. 임의의 ε>0에 대해 1/K <ε/2n 을 만족하는 K(자연수)가 존재한다고 하고 P는 위와 같이 택하면 됩니다. 그러면 일단 적분가능은 보여집니다.
-
답댓글 작성자mathshin 작성자 본인 여부 작성자 작성시간 21.02.06 김성희 넵 감사합니다~!
-
작성자쭈니99 작성시간 21.02.05 리만적분가능하면 적분값은 하적분값과 같기 때문에 하적분값을 구하는 것에 초점을 맞춰보도록 하죠.
P_(n+1)이 P_n의 세분할이라면 L(f,P_(n+1))<=L(f,P_n)이 되므로 L(f, P_n)은 증가수열이 됩니다. 따라서 limL(f,P_n)=sup{L(f,P_n)|P_n in P[0,1]}=(하적분의 정의)가 되므로
위의 등식이 성립합니다