유제4-10, 유제4-12

[궁금]

1. A와 B에서 (1/x,0)과 (1/x,x)로 어떻게 넘어간건가요?
2. 그걸 어떻게 이용해서 부등식 및 d(A,B)를 구했나요?
3.B의 원소는 (0,무한)으로 주어져있는데 R로 어떻게 포함시켰나요?

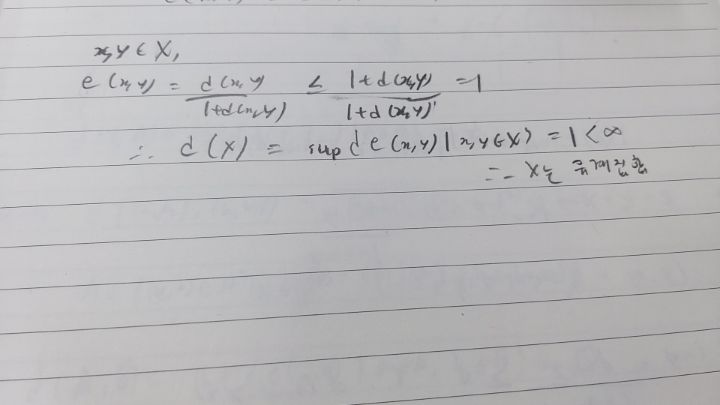
4.유제4-12에서 유계인 거리공간을 증명하라 했는데 유계집합과 거리공간만 알고있어서 질문합니다. 이렇게 X를 유계집합임을 보이면 그게 유계인 거리공간이 된다고 말할수있나요?

5. 문제에서 거리함수 e(답지는d_1이라 표기됨)를 유계거리라고 적고 끝맺었는데 그게 유계인 거리공간임을 어떻게 보인건가요?

[수정과]

①,② x>0에 대해 x=d((1/x,0),(1/x,x))∈{d((a,0),(b,1/b)) | a∈ℝ,b∈(0,∞)}이므로 하한의 정의에 의해 d(A,B)≤x가 성립합니다. 즉 x>0인 임의의 x에 대해 0≤d(A,B)≤x이므로 d(A,B)=0가 성립함을 알 수 있습니다. (임의의 ε>0에 대해 0≤A≤ε ⇒ A=0 은 해석학에서 종종 쓰였던 내용입니다.)
③ y∈(0,∞)가 맞습니다. 해당 부분은 수정 요청하도록 하겠습니다. 알려주셔서 감사합니다.
④ e가 거리함수인지 아닌지 모르는 상황이므로 거리함수가 됨을 같이 보여야 합니다.
⑤ 거리공간 (X,e)에 대하여 e(X)<∞이면 이를 유계인 거리공간이라 합니다.