삼각비 문제인데요

[ss아자아자ss]

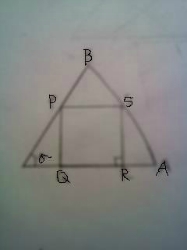
그림과 같이 중심각의 크기가 a인 부채꼴에 내접하는 정사각형 PQRS의 넓이가 25일 때

원 O의 반지름의 길이를 구하여라. (단, tan a=5/3, a는 예각)

답이 루트 89인데 풀이과정 좀 부탁드립니다.

그리고

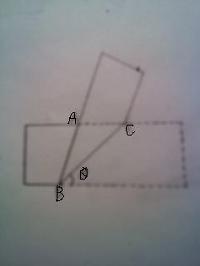
다음 그림과 같이 폭이 6으로 일정한 직사각형을 선분 BC를 접는 선으로 접었다.

sin Θ=3/5일 때, 삼각형 ABC의 값을 구하여라

답이 75/4인데 이것도 부탁드립니다.

[오대감]

[1]
부채꼴의 원점을 O라 하면, 문제에 주어진 단서에 의해 OQ, QR, RS의 길이를 각각 구할 수 있습니다.
OR과 RS의 길이를 가지고 피타고라스 정리를 쓰면 부채꼴의 반지름인 OS의 길이를 구할 수 있겠지요.

[2]
직사각형을 접어서 완전히 겹쳐져 생기는 삼각형은 항상 이등변삼각형이라는 것을 알면 쉽게 해결됩니다.
∠ABC = ∠ACB = θ 가 항상 성립하니까요.
문제에 주어진 단서들을 통해 BC의 길이와 θ의 tan 값을 알 수 있으므로 삼각형의 넓이를 구할 수 있습니다.

[ss아자아자ss]

tan값과 BC의 길이는 구했는데 삼각형의 넓이를 못 구하겠어요;;
2번 문제 풀이과정을 좀더 자세하게 알려주시면 안될까요??

[오대감]

tanθ = 3/4 인 것을 알고, BC=10 인 것을 압니다.
또한, △ABC 가 이등변삼각형인 것을 알고, 밑각의 크기가 θ인 것을 압니다.
이제, 꼭지점 A와 밑변인 BC의 중점을 연결해봅시다.

그러면 실마리가 보이겠지요?

[ss아자아자ss]

감사합니다.