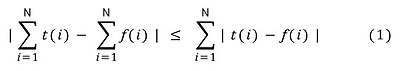
위에 등식은 코시부등식( 또는 삼각부등식으로 ) 으로 성립이 됩니다.
여기서 좌변은 우변과 유사한 값, 즉, 근사값을 가집니다.
제가 궁금한건 다음과 같습니다.
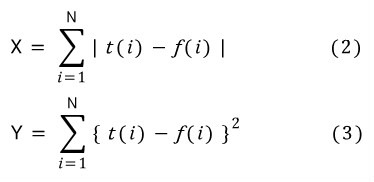
제가 하고싶은건 식(3)을 식 (2)에 근사하고 싶다는겁니다.
즉, 식 (1)과 같이 부등식을 이용해서 근사하고싶습니다.
첫째로, 식(3)에 루트를 씌우면, 식 (2)에 근사될까요 ?
아니면 둘째로, 다음과 같이 N으로 나누고, 루트를 씌어볼까요 ?
식으로 쓰면 다음과 같습니다.
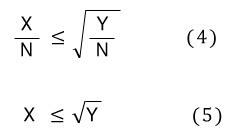
여기서 일단 짚고 넘어가야 하는게, 부등식이 성립을 하느냐 입니다.
여러가지 값을 넣어서 해본결과 성립을 하는것 같습니다. 증명까지는 해주면 좋지만.. 힘드시면 안해주셔도 됩니다.
또한 궁금한게, 식(4)를 이용하면, 우변은 좌변에 근사가 되느냐 입니다.
좌변과 우변의 결과값의 차이가 심하게 나는지, 아니면, 그리 차이가 나지 않는지 입니다.
여기서 이 차이를 갭이라고 합시다. 거리라구 해도 좋구요.
참고로 말하자면 t(i)와 f(i)의 값은 정수라고 가정합니다. 그리고 N은 보통 5000 정도로 생각하면 좋습니다
식 (4)의 좌변과 우변의 갭과
식 (5)의 좌변과 우변의 갭이, 어느쪽이 더 작아질까 입니다.
제 생각엔 식(4)의 경우가 갭이 더 작아질것 같은데, 선뜻 잘 모르겠네요. 하나하나 데이터로 실험을 해볼까도 생각중인데, 그냥 여러분들의 생각을 듣고싶습니다.
또한 이 아이디어 이외에도,
식 (3)으로 식(2)에 근사할수 있는 방법이 뭐가 있는지도 궁금합니다.