[선택미적]삼각함수 합성 -> 원으로해결 [질문]

[레프트_fitch]

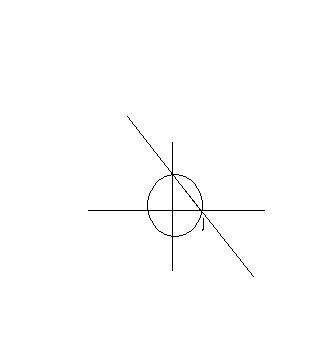
sin x + cos x = 1 을

 그래프로 푸는형태

↓↓

cos x ,sin x  =>  반지름 1 원의 점(X,Y) 으로 둘수있기때문에

아래처럼 반지름1 원으로 나타냄

여기서

sin x + cos x = 1  =>  X +Y =1

X,Y의 해는 원과 X +Y =1교점에서

(1,0) (0,1)

각각

<sin x = 0 // cos x = 1> , <cos x = 0 // sin x =1>

로 두고 근을 구하려 했습니다.

그런데 에서<sin x = 0 // cos x = 1>

sin x 에서 근은 0 ,π, 2π

cos x 에서는 π, 2π

근이 동시에 같이 나와야하는데 (둘다 0 ,π, 2π이런식으로 나와야된다고 생각)

지금 뭘하고있는지 헷갈리네요

정정해주시고

==========================

다른 정석풀이로는

원과 직선의 교점이 (1,0) ,(0,1)

구하고 바로

x= 2nπ , 2nπ+π/2

원에서 바로 교점의 동경을 보고 , 그걸 답으로 바로해버린겁니다.

===========================

이해하기 좀 어렵네요

제대로 아시는분만 답변바랍니다.

[MC HK]

첫번째 풀이에서 sinx=0, cosx=1 을 동시에 만족하는 근을 찾아야죠~ 일반해는 무수히 많은데 거기서 두 식을 동시에 만족하는것.. 이 해겠죠!! 꼭 일반해를 푼것이 같은 근이 나와야 할수는 없죠. 그리고 위쪽풀이에서 cosx 의 근을 구하는데 pi 는 해가 아니죠.. // 아래 풀이는 sinx=0, cosx=1 을 동시에 만족하는 x의 일반해를 표시한겁니다.. 위 풀이보다 더 비약이죠

[MC HK]

비약이라기 보다는 생략