▣ 주성분 분석의 원리1.
쉬운 설명:
■ 1. 주성분 분석(PCA)란?
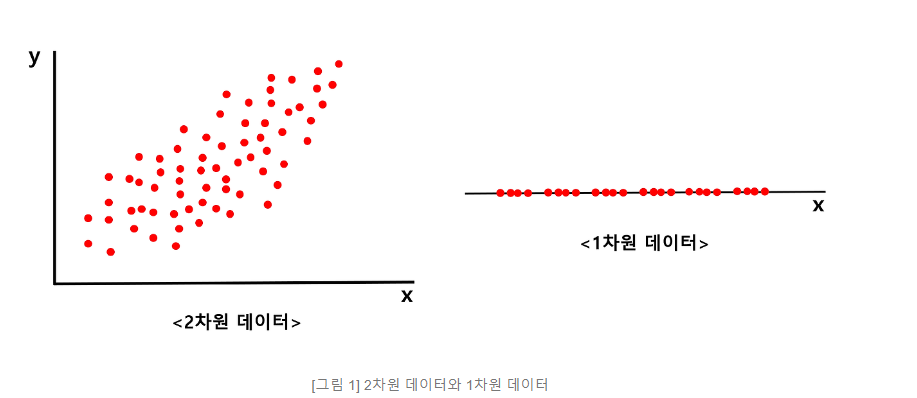
고차원의 데이터를 낮은 차원의 데이터로 변환하여, 머신러닝, 데이터마이닝, 통계 분석, 노이즈 제거 등 다양한 분야에서 사용됩니다.
■ 2. 왜 중요할까?
데이터가 간단해져 이해하기 쉬워지고, 저장 공간도 절약됩니다. 예를 들어, 학생들의 성적(국어, 수학, 영어 등)에서 중요한 정보를 쉽게 찾을 수 있습니다.
■ 3. 예를 들어보면?
예시: 학생 성적 분석
- PC1: 학생들의 전반적인 학업 성취도를 나타냅니다. 모든 과목에서 높은 점수를 받은 학생들이 높은 PC1 점수를 갖습니다.
- PC2: 특정 과목에 대한 성취도를 나타냅니다. 예를 들어, 수학에서 높은 점수를 받은 학생들이 높은 PC2 점수를 갖습니다.
요약:
- PC1: 전체 성적이 높은 학생들.
- PC2: 특정 과목에서 두드러지는 학생들.
PCA는 학생들의 성적 데이터에서 중요한 패턴을 찾아내어 학습 성과를 효과적으로 분석하는 데 도움을 줍니다.
모든 과목이 3과목이고 국어,영어,수학이 있다고 하고 국어(X축), 수학(Y축), 영어(Z축) 이라고 하자
그러면 PC1 은 국어,수학,영어를 가장 잘 설명하는 어느 직선이 된다.
구현 R 코드:
| # 필요한 패키지 설치 및 로드 install.packages("ggplot2") install.packages("plotly") install.packages("scatterplot3d") library(ggplot2) library(plotly) library(scatterplot3d) # 데이터 생성 set.seed(123) # 재현성을 위해 시드 설정 num_students <- 100 data <- data.frame( 국어 = rnorm(num_students, mean = 70, sd = 10), 수학 = rnorm(num_students, mean = 65, sd = 12), 영어 = rnorm(num_students, mean = 75, sd = 8) ) # 주성분 분석 수행 pca_result <- prcomp(data, scale. = TRUE) # 주성분 점수 추출 pca_scores <- data.frame(pca_result$x) # 주성분 방향 벡터 pc1_vector <- pca_result$rotation[,1] # 데이터의 중심 계산 center <- colMeans(data) # 3D 시각화 s3d <- scatterplot3d(data$국어, data$수학, data$영어, pch = 19, color = "blue", main = "3D PCA Plot", xlab = "국어", ylab = "수학", zlab = "영어") # 주성분 벡터 그리기 (데이터 중심을 기준으로 양쪽 방향) s3d$points3d(center[1] + pc1_vector[1] * c(-10, 10), center[2] + pc1_vector[2] * c(-10, 10), center[3] + pc1_vector[3] * c(-10, 10), type = "l", col = "red", lwd = 3) # Plotly를 사용한 인터랙티브 시각화 plot_ly(x = ~data$국어, y = ~data$수학, z = ~data$영어, type = 'scatter3d', mode = 'markers', marker = list(size = 3, color = 'blue')) %>% add_trace(x = center[1] + pc1_vector[1] * c(-10, 10), y = center[2] + pc1_vector[2] * c(-10, 10), z = center[3] + pc1_vector[3] * c(-10, 10), type = 'scatter3d', mode = 'lines', line = list(color = 'red', width = 5)) %>% layout(scene = list(xaxis = list(title = '국어'), yaxis = list(title = '수학'), zaxis = list(title = '영어'), title = "3D PCA Plot with PC1")) |
####################################################################################
위의 설명에서 PC1 의 직선 찾는 방법:
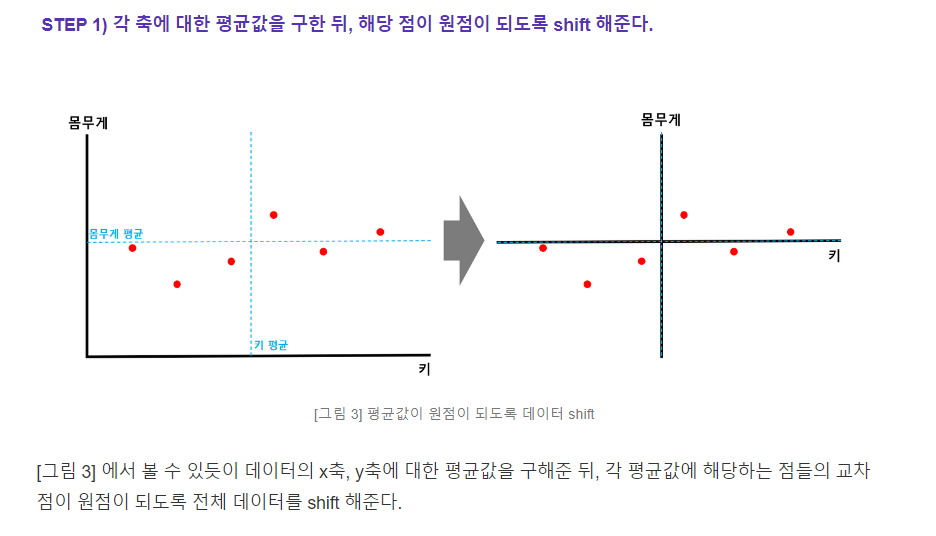
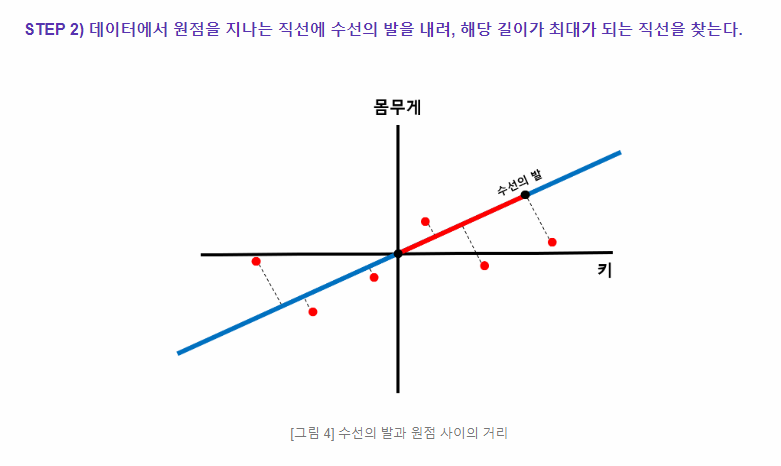
step3) 수직 거리(빨간색 선)의 길이 합이 최소가 되는 녹색 직선을 찾는다.
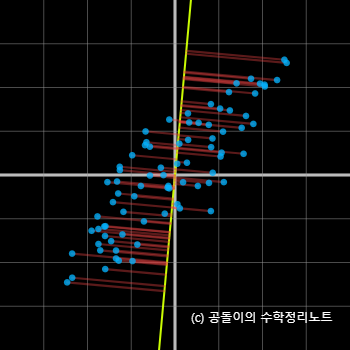
이미지에서 빨간색 선은 각 점에서 녹색 직선(주성분 축)까지의 수직 거리를 나타냅니다.
주성분 분석(PCA)의 목적은 이러한 수직 거리(빨간색 선)의 길이 합이 최소가 되는 녹색 직선을 찾는 것입니다.
이 녹색 직선은 데이터의 분산이 가장 큰 방향을 나타내며, 데이터를 가장 잘 설명하는 축입니다.
이 축을 따라 데이터를 투영하면, 데이터의 주요 패턴을 가장 잘 보존하면서 차원을 줄일 수 있습니다.
컬럼들의 갯수로 정리하면 ?
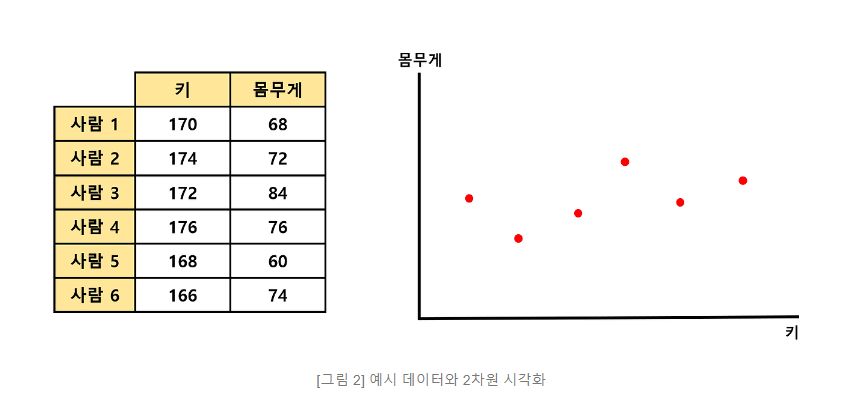
1. (컬럼2개) 체중과 키:
2차원 데이터를 1차원으로 줄이기 위해 첫 번째 주성분(PC1)을 구합니다.
PC1은 체중과 키의 변동성을 가장 잘 설명하는 방향을 나타냅니다.
2. (컬럼3개) 국어, 영어, 수학 성적:
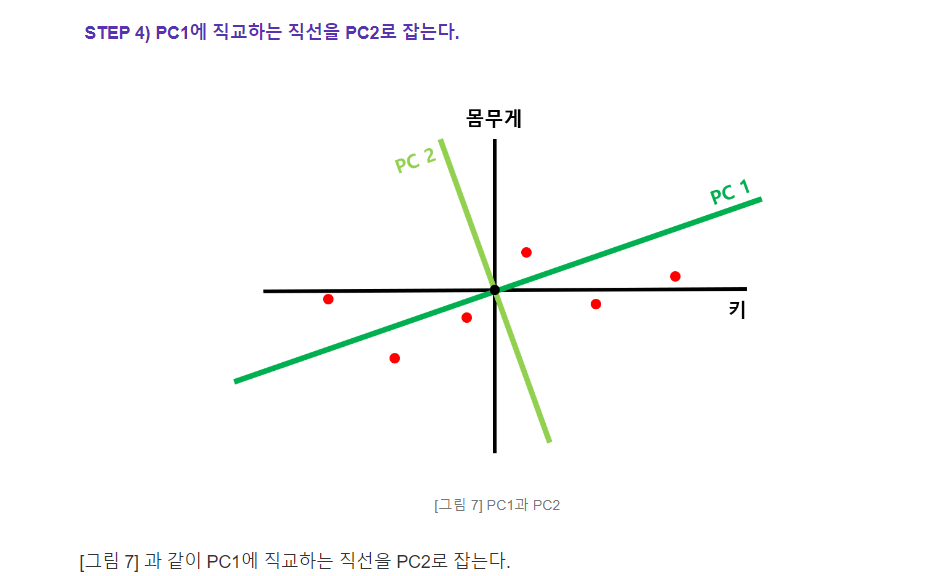
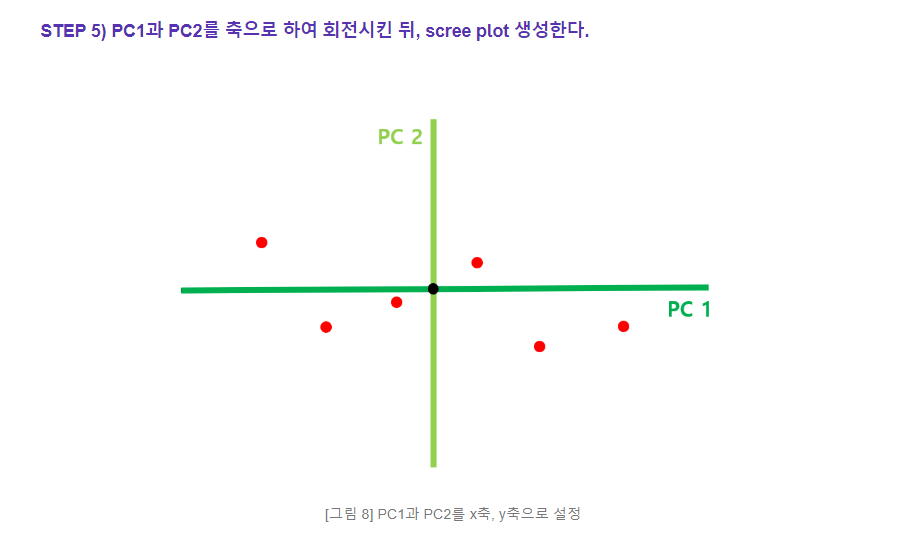
3차원 데이터를 2차원으로 줄이기 위해 첫 번째 주성분(PC1)과 두 번째 주성분(PC2)을 구합니다.
PC1은 전반적인 학업 성취도를 나타내고, PC2는 특정 과목에서의 성취도를 나타냅니다.
이 과정을 통해 데이터의 주요 패턴을 유지하면서 차원을 축소할 수 있습니다.
3. (컬럼4개) 아이리스(iris)
아이리스 데이터셋을 예로 들어, 주성분 분석(PCA)을 통해 4차원 데이터를 2차원으로 축소
데이터 설명:
아이리스 데이터셋에는 다음과 같은 4개의 독립변수가 있습니다:
Sepal.Length (꽃받침 길이)
Sepal.Width (꽃받침 너비)
Petal.Length (꽃잎 길이)
Petal.Width (꽃잎 너비)
코드:
| # 필요한 패키지 설치 및 로드 install.packages("ggplot2") install.packages("plotly") library(ggplot2) library(plotly) # 아이리스 데이터셋 로드 iris_data <- read.csv("c:\\data\\iris2.csv") # 주성분 분석 수행 pca_result <- prcomp(iris_data[, 1:4], scale. = TRUE) # 주성분 점수 추출 pca_scores <- data.frame(pca_result$x) pca_scores$Species <- iris_data$Species # 2차원 시각화 p <- ggplot(pca_scores, aes(x = PC1, y = PC2, color = Species)) + geom_point(size = 3) + labs(title = "PCA 결과", x = "PC1", y = "PC2") + theme_minimal() # plotly를 사용한 인터랙티브 시각화 p_interactive <- ggplotly(p) # 시각화 출력 p_interactive |
코드를 보면 pc3 도 있고 pc4 도 있는데 이는 무엇인가?
국어, 영어, 수학, 과학 4과목을 예로 들어 주성분 분석(PCA)을 쉽게 설명해볼게요.
주성분 분석을 통해 이 4개의 과목 성적을 분석하면, PC1, PC2, PC3, PC4의 의미를 다음과 같이 이해할 수 있습니다.
주성분 분석의 의미PC1 (첫 번째 주성분):
- 설명: 데이터의 가장 큰 변동성을 설명하는 축입니다.
- 쉽게 설명: 모든 과목에서 높은 점수를 받은 학생들은 PC1 값이 높습니다. 반대로 모든 과목에서 낮은 점수를 받은 학생들은 PC1 값이 낮습니다.
- 의미: PC1은 학생들의 전반적인 학업 성취도를 나타냅니다. 즉, 전체 성적이 얼마나 우수한지를 보여줍니다.
PC2 (두 번째 주성분):
- 설명: PC1과 직교하며, 남은 변동성 중 가장 큰 부분을 설명합니다.
- 쉽게 설명: PC1에서 설명하지 못한 부분을 추가로 설명합니다. 예를 들어, 수학과 과학에서 높은 점수를 받은 학생들은 PC2 값이 높을 수 있습니다.
- 의미: PC2는 특정 과목 조합에서의 차이를 나타냅니다. 예를 들어, 수학과 과학에 특화된 성취도를 보여줍니다.
PC3 (세 번째 주성분):
- 설명: PC1과 PC2에 직교하며, 남은 변동성 중 세 번째로 큰 부분을 설명합니다.
- 쉽게 설명: PC1과 PC2에서 설명하지 못한 더 세부적인 변동성을 설명합니다. 예를 들어, 국어와 영어에서 특정한 패턴을 보이는 학생들이 있을 수 있습니다.
- 의미: PC3는 또 다른 과목 조합에서의 성취도를 나타냅니다. 예를 들어, 국어와 영어에 특화된 성취도를 보여줍니다.
PC4 (네 번째 주성분):
- 설명: PC1, PC2, PC3에 직교하며, 남은 변동성 중 네 번째로 큰 부분을 설명합니다.
- 쉽게 설명: 남아 있는 가장 적은 변동성을 설명합니다. 예를 들어, 과학에서만 두드러진 성취도를 보이는 학생들이 있을 수 있습니다.
- 의미: PC4는 가장 적은 변동성을 설명하며, 매우 세부적인 패턴을 나타냅니다.
요약
- PC1: 전체 과목에서 전반적으로 높은 성적을 가진 학생들의 성취도를 나타냅니다.
- PC2: 특정 과목 조합 (예: 수학과 과학)에서의 성취도를 나타냅니다.
- PC3: 다른 특정 과목 조합 (예: 국어와 영어)에서의 성취도를 나타냅니다.
- PC4: 나머지 가장 적은 변동성을 설명하며, 특정 과목에서의 세부적인 패턴을 나타냅니다.
주성분 분석을 통해 학생들의 성적 데이터를 분석하면, 각 주성분이 데이터의 주요 패턴을 어떻게 설명하는지 알 수 있습니다. 이를 통해 복잡한 데이터에서 중요한 정보를 추출하고 이해하기 쉽게 만들 수 있습니다.
문제. 유방암(wisc_bc_data.csv) 데이터를 주성분 분석해서 2차원으로 시각화 하시오!
그림설명이 많은 참고자료:
https://ddongwon.tistory.com/114