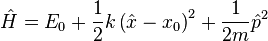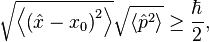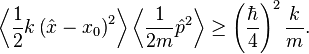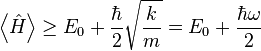오늘 이걸 위키에서 찾아서 읽다가 수식전개에서 막히는 부분이 있어서 설명좀 부탁드립니다 ㅠㅠ
Relation to the uncertainty principle
Zero-point energy is fundamentally related to the Heisenberg uncertainty principle. Roughly speaking, the uncertainty principle states that complementary variables (such as a particle's position and momentum, or a field's value and derivative at a point in space) cannot simultaneously be defined precisely by any given quantum state. In particular, there cannot be a state in which the system sits motionless at the bottom of its potential well, for then its position and momentum would both be completely determined to arbitrarily great precision. Therefore, the lowest-energy state (the ground state) of the system must have a distribution in position and momentum that satisfies the uncertainty principle, which implies its energy must be greater than the minimum of the potential well.
Near the bottom of a potential well, the Hamiltonian of a system (the quantum-mechanical operator giving its energy) can be approximated as
where E0 is the minimum of the classical potential well. The uncertainty principle tells us that
making the expectation values of the kinetic and potential terms above satisfy
The expectation value of the energy must therefore be at least
- 이부분이 막혀요 ㅠ위에 식에서 아래 식으로 내려가는 중간과정 설명좀 부탁드립니다 ㅠ
- ..늘.. 수식전개가 문제네요 ㅠ
where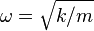 
is the angular frequency at which the system oscillates.
A more thorough treatment, showing that the energy of the ground state actually is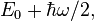 
requires solving for the ground state of the system. See quantum harmonic oscillator for details.
출처 http://en.wikipedia.org/wiki/Zero-point_energy
사실 위에 Eo가 왜 나오는지도 의문입니다 ㅠ 처음부터 Eo를 가정하고 출발해도 되는건가요?