solid figure
입체 도형
plane figure
평면 도형
two dimensional figure
2차원(평면) 도형
http://koreajoongangdaily.joins.com/news/article/article.aspx?aId=2889615
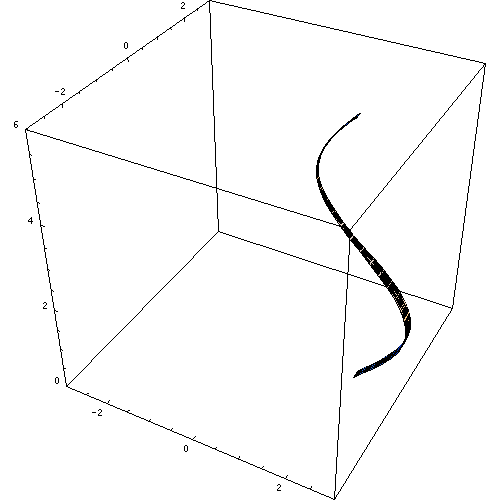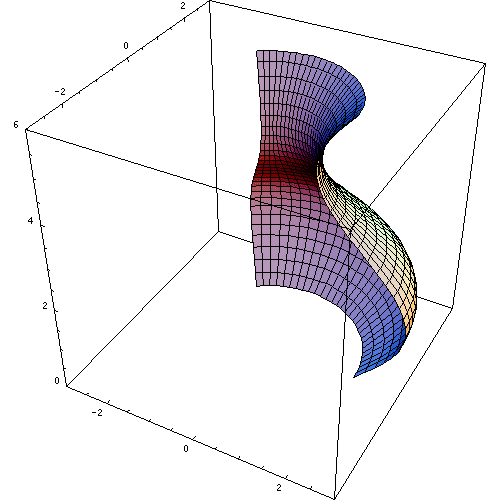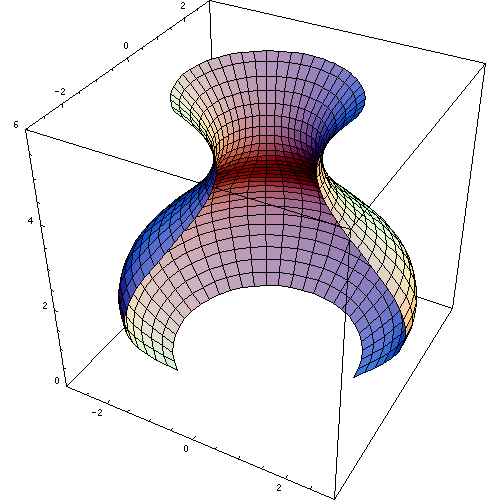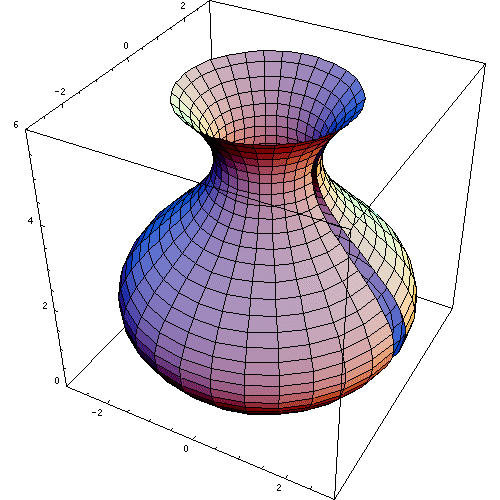
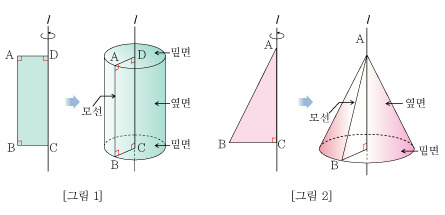
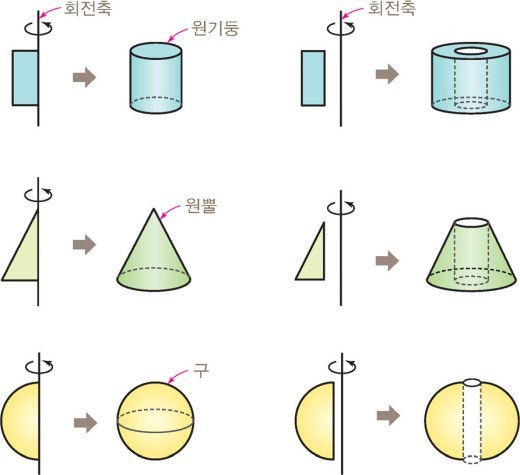
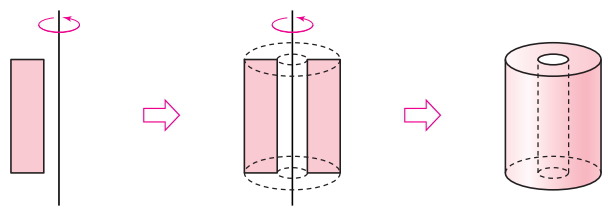
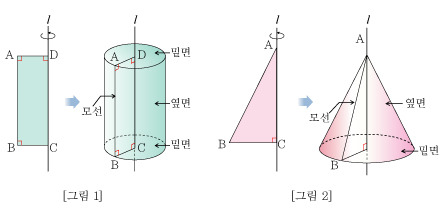
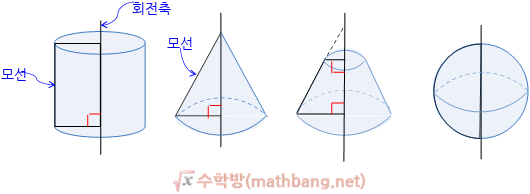
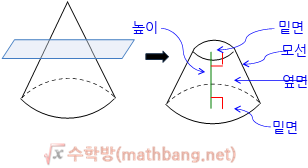
a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line (the axis of revolution) that lies on the same plane.
Solid of revolution
Rotating a curve. The surface formed is a surface of revolution; it encloses a solid of revolution.
Solids of revolution
In mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curvearound some straight line (the axis of revolution) that lies on the same plane.
Assuming that the curve does not cross the axis, the solid's volume is equal to the lengthof the circle described by the figure's centroidmultiplied by the figure's area (Pappus's second centroid Theorem).
A representative disk is a three-dimensionalvolume element of a solid of revolution. The element is created by rotating a line segment(of length w) around some axis (located runits away), so that a cylindrical volume of πr2w units is enclosed.
Finding the volume
Two common methods for finding the volume of a solid of revolution are the disc method and the shell method of integration. To apply these methods, it is easiest to draw the graph in question; identify the area that is to be revolved about the axis of revolution; determine the volume of either a disc-shaped slice of the solid, with thickness δx, or a cylindrical shell of width δx; and then find the limiting sum of these volumes as δxapproaches 0, a value which may be found by evaluating a suitable integral.
Disk method

Disk integration about the y-axis
Main article: Disc integration
The disk method is used when the slice that was drawn is perpendicular to the axis of revolution; i.e. when integrating parallel to the axis of revolution.
The volume of the solid formed by rotating the area between the curves of f(x) and g(x) and the lines x = a and x = b about the x-axis is given by
{displaystyle V=pi int _{a}^{b}left|f(x)^{2}-g(x)^{2}right|,dx,.}
If g(x) = 0 (e.g. revolving an area between the curve and the x-axis), this reduces to:
{displaystyle V=pi int _{a}^{b}f(x)^{2},dx,.}
The method can be visualized by considering a thin horizontal rectangle at y between f(y)on top and g(y) on the bottom, and revolving it about the y-axis; it forms a ring (or disc in the case that g(y) = 0), with outer radius f(y) and inner radius g(y). The area of a ring is π(R2 − r2), where R is the outer radius (in this case f(y)), and r is the inner radius (in this case g(y)). The volume of each infinitesimal disc is therefore πf(y)2 dy. The limit of the Riemann sum of the volumes of the discs between a and b becomes integral (1).
Cylinder method
Main article: Shell integration

Shell integration
Solid of revolution demonstration

The shapes at rest

The shapes in motion, showing the solids of revolution formed by each
The cylinder method is used when the slice that was drawn is parallel to the axis of revolution; i.e. when integrating perpendicular to the axis of revolution.
The volume of the solid formed by rotating the area between the curves of f(x) and g(x) and the lines x = a and x = b about the y-axis is given by
{displaystyle V=2pi int _{a}^{b}x|f(x)-g(x)|,dx,.}
If g(x) = 0 (e.g. revolving an area between curve and y-axis), this reduces to:
{displaystyle V=2pi int _{a}^{b}x|f(x)|,dx,.}
The method can be visualized by considering a thin vertical rectangle at x with height f(x) − g(x), and revolving it about the y-axis; it forms a cylindrical shell. The lateral surface area of a cylinder is 2πrh, where r is the radius (in this case x), and h is the height (in this case f(x) − g(x)). Summing up all of the surface areas along the interval gives the total volume.
Parametric formEdit

Mathematics and art: study of a vase as a solid of revolution by Paolo Uccello. 15th century
When a curve is defined by its parametric form (x(t),y(t)) in some interval [a,b], the volumes of the solids generated by revolving the curve around the x-axis or the y-axis are