http://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula
Rodrigues' rotation formula
From Wikipedia, the free encyclopedia
| This article may require cleanup to meet Wikipedia's quality standards. Please improve this article if you can. (March 2008) |
In geometry, Rodrigues' rotation formula (named after Olinde Rodrigues) is a vector formula for a rotation in space, given its axis and angle of rotation.
Say u,v
 R3 and we want to obtain a representation for the rotation vrot of the vector v around the vector u (which is assumed to have unit length) by an angle θ in the counterclockwise (i.e. positive) direction. Rodrigues' formula reads as follows:
R3 and we want to obtain a representation for the rotation vrot of the vector v around the vector u (which is assumed to have unit length) by an angle θ in the counterclockwise (i.e. positive) direction. Rodrigues' formula reads as follows:
[edit] Proof of the formula
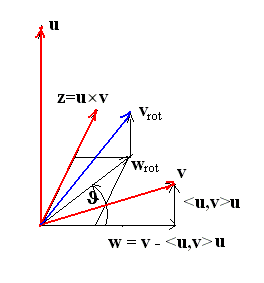
Take the vector w = v − <u,v>u, which is the projection of v on the plane orthogonal to u, and the cross product of the vectors u and v: z = u×v. Turn the vector w by the angle θ around the base of the vector u to obtain the projection of the rotated vector vrot:
Notice that both the vectors w and z have the same length: |w|,|z| = |v - <u,v>u|, because the vector u is of unit length. To get the rotated vector v, we have to add back the adjustment <u,v>u. Hence
which is exactly what we were looking for.
Using the notation
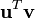 for the scalar product, we get:
for the scalar product, we get:
Denoting by
![\left[ \mathbf{u} \right]_\times](https://img1.daumcdn.net/relay/cafe/R400x0/?fname=http%3A%2F%2Fupload.wikimedia.org%2Fmath%2F5%2F5%2F6%2F5563fb81352e634208a3665fd7c2bf9a.png) the "cross-product" matrix for
the "cross-product" matrix for
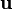 , i.e.
, i.e.
the cross-product
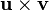 can be represented with the matrix product
can be represented with the matrix product
![\left[ \mathbf{u} \right]_\times \mathbf{v}](https://img1.daumcdn.net/relay/cafe/R400x0/?fname=http%3A%2F%2Fupload.wikimedia.org%2Fmath%2F6%2F5%2F0%2F6508bfa8f0ace4bac78bc8c46757122d.png) and we have
and we have
where I is the 3x3 identity matrix. The expression in the parenthesis can be identified as the rotation matrix R:
Considering that
![\mathbf{u} \mathbf{u}^T = \left[ \mathbf{u} \right]_\times^2 + I](https://img1.daumcdn.net/relay/cafe/R400x0/?fname=http%3A%2F%2Fupload.wikimedia.org%2Fmath%2F8%2Fe%2Fc%2F8ec6c7fbaa9c2aea05dc7b7f84b38469.png) , the expression for the rotation matrix R is sometimes written as
, the expression for the rotation matrix R is sometimes written as
or, equivalently,
[edit] See also
[edit] External links
- For another descriptive example see www.d6.com, Chris Hecker, physics section, part 4. "The Third Dimension" -- on page 3, section ``Axis and Angle, http://www.d6.com/users/checker/pdfs/gdmphys4.pdf
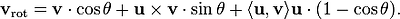
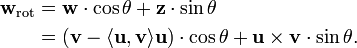
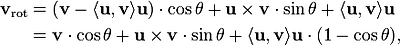
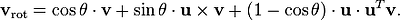
![\begin{align}
\left[ \mathbf{u} \right]_\times &=
\left(\begin{array}{ccc}
0 & -u_3 & u_2 \\
u_3 & 0 & -u_1 \\
-u_2 & u_1 & 0
\end{array}\right),
\end{align}](https://img1.daumcdn.net/relay/cafe/R400x0/?fname=http%3A%2F%2Fupload.wikimedia.org%2Fmath%2Fc%2F9%2F4%2Fc948d5a2095fbce2bc294df8df9aaf97.png)
![\begin{align}
\mathbf{v}_{\mathrm{rot}} &= \cos\theta \cdot I \mathbf{v} + \sin\theta \cdot \left[ \mathbf{u} \right]_\times \mathbf{v}
+ (1 - \cos\theta) \cdot \mathbf{u} \cdot \mathbf{u}^T \mathbf{v} \\ &=
\left( \cos\theta I + \sin\theta \left[ \mathbf{u} \right]_\times
+ (1 - \cos\theta) \mathbf{u} \mathbf{u}^T \right) \mathbf{v},
\end{align}](https://img1.daumcdn.net/relay/cafe/R400x0/?fname=http%3A%2F%2Fupload.wikimedia.org%2Fmath%2F0%2F4%2Fd%2F04d8fc70cb31041b8d3c11a910ff49ae.png)
![\begin{align}
R = \cos\theta I + \sin\theta \left[ \mathbf{u} \right]_\times + (1 - \cos\theta) \mathbf{u} \mathbf{u}^T.
\end{align}](https://img1.daumcdn.net/relay/cafe/R400x0/?fname=http%3A%2F%2Fupload.wikimedia.org%2Fmath%2F9%2Fe%2Fd%2F9ed09ed4abfd154ff2690936f318fbd3.png)
![\begin{align}
R = I + \sin\theta \left[ \mathbf{u} \right]_\times + (1 - \cos\theta) \left[ \mathbf{u} \right]_\times^2
\end{align}](https://img1.daumcdn.net/relay/cafe/R400x0/?fname=http%3A%2F%2Fupload.wikimedia.org%2Fmath%2F8%2Fc%2Fa%2F8cab7e4df87a97bdbdace90c56256191.png)
![\begin{align}
R = I + \sin\theta \left[ \mathbf{u} \right]_\times + (1 - \cos\theta) (\mathbf{u} \mathbf{u}^T - I).
\end{align}](https://img1.daumcdn.net/relay/cafe/R400x0/?fname=http%3A%2F%2Fupload.wikimedia.org%2Fmath%2Fd%2F1%2Fa%2Fd1af4503e730d0091d4a720d39aa5050.png)
![[costheta+omega_x^2(1-costheta) omega_xomega_y(1-costheta)-omega_zsintheta omega_ysintheta+omega_xomega_z(1-costheta); omega_zsintheta+omega_xomega_y(1-costheta) costheta+omega_y^2(1-costheta) -omega_xsintheta+omega_yomega_z(1-costheta); -omega_ysintheta+omega_xomega_z(1-costheta) omega_xsintheta+omega_yomega_z(1-costheta) costheta+omega_z^2(1-costheta)],](https://img1.daumcdn.net/relay/cafe/R400x0/?fname=http%3A%2F%2Fmathworld.wolfram.com%2Fimages%2Fequations%2FRodriguesRotationFormula%2FInline10.gif)
![omega^~=[0 -omega_z omega_y; omega_z 0 -omega_x; -omega_y omega_x 0].](https://img1.daumcdn.net/relay/cafe/R400x0/?fname=http%3A%2F%2Fmathworld.wolfram.com%2Fimages%2Fequations%2FRodriguesRotationFormula%2FNumberedEquation1.gif)