화학 1에서는 주양자수가 n일때
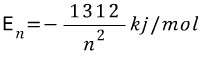
라고 소개하고 있습니다.
이 식을 이해하기 위해서는 전자의 파동적 성질을 이용해야 하는데,
화학1에서는 파동함수는 커녕 결맞은 파동으로 인해 전자궤도가 유지된다는것도 안나와있습니다.
보어 입장에서도 긴가민가 했겠지만(당시에 입자성과 파동성의 공존은 상당히 파격적이었으므로)
일단 수소원자 스펙트럼이 잘 설명되니까 그런가보다 했을겁니다.
그럼 우리가 할 일은 뭐냐면, 화학1의 수준으로 저 위에 달라붙는 이상한 상수부터 어떻게 좀 해봅시다.
전자가 가지는 전자기적 궤도 에너지를 구한 뒤에 위의 식과 비교합시다.
우선 쿨롱의 법칙은 아래와 같습니다.
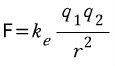
(k_e=쿨롱 상수, r은 두 전하 사이의 거리, q는 각 전하의 크기)
화학1 수준으로 증명하자고 했으면서 쿨롱의법칙이 화1에 나오냐고 물으면 그다지 할말은 없지만
적어도 보어는 알고있었을테니까요.
이제 거리에 따른 전기적 위치에너지를 나타내는 함수 P(r)을 구해봅시다.
무한대 거리에 있을때 전위가 0이 되어야 한다는것을 생각하며, r에서 ∞까지 적분해 봅시다.
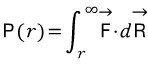
네이버는 벡터표기가 별로 이쁘지 않다는걸 알았습니다.
힘벡터의 방향과 r의 방향이 반대이므로 내적하면 마이너스가 붙겠네요.
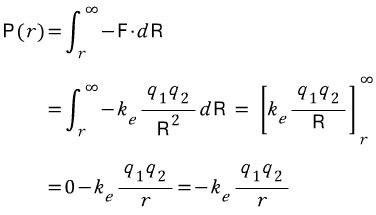
그렇다고 합니다.
사실 그냥 중력에 의한 위치에너지랑 별로 다를 바 없네요.
이제 운동에너지 K(r)을 구해봅시다. 가정에서 전자가 궤도를 등속원운동한다고 했죠.
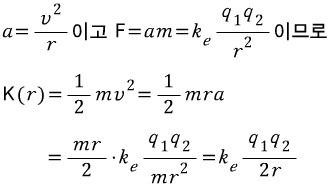
ㅇㅇ그러합니다. m이 없어져서 기분이 좋군요!
이제 거리 r에 따른 에너지를 구해봅시다. 그냥 위에꺼 두개 더해보죠.
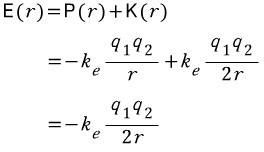
호옹이! 좋쿠나!
그런데 화학1책에서
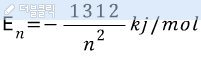
라고 했습니다. 제대로 추측했다면 두 En=E(r)이 되어야겠지요.
위에 달린 상수를 k로 취급하겠습니다.
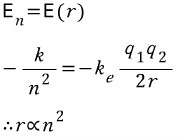
그런고로 궤도의 반지름이 주양자수의 제곱에 비례한다는걸 알 수 있습니다.
이건 꽤 중요한데, 저희 교과서가 안좋은건지 어쩐지는 모르겠지만
책의 그림만 봐서는 주양자수의 제곱근에 반지름이 비례한다고 착각할수도 있습니다(제가 그랬습니다 ㅋㅋ)
이제 우리가 그토록 찾고싶던 k를 얻을 수 있겠군요! 언능 정리해봅시다 궈궈

(N_a=아보가드로상수, R_k=K껍질의 반지름)
내친김에 계산까지 해보죠.
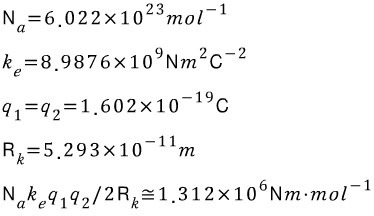
끝
단위전환을 안한다면 물리에서 많이쓰이는 전자볼트(eV)단위로 구할수도 있습니다.
파동함수도 공부해서 오비탈도 증명하면 재밌을것같습니다.