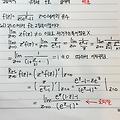[복소 해석학]극점의 유수

[스리]

교수님 m차 극점에서의 유수를 구하다가 궁금한 점이 생겼습니다.
예를들어 0에서의 유수를 구할 때 (z^m)f(x)을 m-1번 미분한 뒤 0을 대입하잖아요.
그런데 제가 어떤 문젤 푸는데 저걸 m-1번 미분한것이 분수형태로 나오고, 0을 대입하려고 봤더니 분모분자가 0이 되더라고여
그래서 0으로 극한을 보내야겠다 생각했는데, 복소범위에서도 로피탈정리를 쓸 수 있나요?(분모 분자가 미분가능해야하니깐, 분모 분자가 극한으로 보내려는 점 근처에서 해석적이기만하면 될 것 같긴한뎁. .)

[스리]

빨간색으로표시한데서 로피탈썼습니다!

[신선물고기]

스리 로피탈 써도 됩니다. 하지만 그림과 같은 스타일이 더욱 좋습니다.

[스리]

신선물고기 교수님 이해는 했는데요
극점인거 이야기할때 일단 '고립특이점이고, 제거가능특이점은 아니다'라는 이야기는 굳이 안해주어도 되는건가요?

[신선물고기]

스리 이차극점이라는 말이 고립특이점이고 제거가능특이점은 아님을 함유하고 있는데요, 이거 물어보신게 맞나 모르겠네요.

[스리]

신선물고기 아 저는 이차 극점의 뜻을 일단 '고립특이점아닌 특이점중에서~' 라고 생각을 했어서 저렇게 여쭤봤습니다.
그런데 며칠 지나고 보니까 저 이야기 안쓰고 그냥 바로 이차극점임을 보여도 될 것 같네욤 ㅎㅎ 감사합니다~