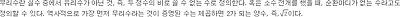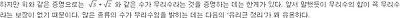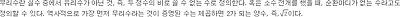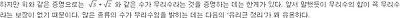
무리수, 두 정수의 비로 쓸 수 없는 수

|
|
|
|

글을 쓰고 있는 피타고라스. 라파엘로의 그림 | |
√2가 무리수라는 것을 보여주는 가장 흔한 증명


√2는 대수적 무리수이다



유한 단계의 연분수는 유리수이다, 그러면 무리수는?

|
(단순)연분수란 주어진 수를 ‘정수부분과 소수부분으로 쪼갠 뒤, 소수부분이 0이 아닐 경우 소수부분의 역수를 다시 정수부분과 소수부분으로 쪼개는 과정’을 반복해서 얻는 수식을 말한다. 예를 들어 유리수 90/17을 생각하자. 이 수를 정수부분과 소수부분으로 쪼개보자.

이제 소수부분만 떼어 내, 역수 17/5을 역시 정수부분과 소수부분으로 쪼개 보자.

마찬가지로 소수부분의 역수인 5/2를 정수부분과 소수부분으로 쪼개 쓰자.

마지막으로 소수부분의 역수 2/1를 역시 쪼개 보자. 이제 소수 부분이 0이 되어 네 단계에 끝난다.

이 과정을 한꺼번에 쓰면 아래와 같은데, 이를 연분수로 나타냈다고 말한다.

아무 유리수나 주고 위의 과정을 적용하면 유한 단계에 끝날 수밖에 없는데, 중간 단계에 등장하는 소수부분의 (위의 예에서는 5/17, 2/5, 1/2) 분모와 분자가 갈수록 작아지기 때문이다. 사실 에르되시(Paul Erdős, 1913-1996)는 ‘유한 단계에 끝나는 연분수가 유리수라는 것은 어린이도 이해할 수 있다’고 말할 정도였는데, 정말로 그러한지는 독자들이 판단할 문제이다. | |
연분수를 써서 √2가 무리수임을 증명하자


연분수를 이용하면 근삿값을 쉽게 찾을 수 있다


- 글 정경훈 / 서울대 기초교육원 강의교수
- 서울대학교 수학과에서 학사, 석사, 박사를 받고, 포항공대, 연세대, 위스콘신대, 서울대에서 박사후 과정을 밟았다. 현재 서울대 기초교육원 강의교수이다.