루트2를 계산해 보자.

[귀뚜라미]

피타고라스 학파가 처음 발견하였다고 전해지는 무리수 √2 (이 글에서 루트2를 의미한다).  이 수가 유리수가 아니라는 것을 증명할 수는 있지만, 이 수가 대략 어떤 값인지를 구하는 것은 또 다른 문제이다. 보통 √2=1.414213⋯라고 하는데, 이 값은 어떻게 구하는 것일까?

바빌로니아 문명의 사람들도 √2를 계산할 수 있었다

√2가 무리수라는 것은 피타고라스 학파에 의해 밝혀졌지만, 비교적 정밀한 근삿값은 훨씬 이전부터 알려져 있었다. 기원전 약 1800년 무렵의 바빌로니아 인들이 남겨 놓은 YBC 7289라고 불리는 점토판이 있다. 거기에는 바빌로니아 인들이 60진법을 이용하여 √2의 근삿값을 기록해 두었다. 이를 10진법으로 고쳐 보면 대략 1.41421356이 되어 소수점 아래 5번째 자리까지 정확하다. 당시 고대의 수학자들은 어떻게 근삿값을 구한 것인지 궁금하지 않을 수 없다.

바빌론의 공중정원과 바벨탑(16세기 화가의 그림)

가장 무식한 방법 - 정의대로!

√2의 정의를 곧이곧대로 이용하여 구하는 것이 가장 쉽게 생각할 수 있는 방법이다. 즉, 제곱해서 2에 가까워지는 수를 찾으면 된다. 먼저, 1² = 1 < 2 < 2² = 4이므로, √2=1.**** 꼴이 된다. 다시 1.1부터 1.9에 대해 제곱을 해 보면, 아래와 같다. 그래서 √2=1.4**** 꼴이 됨을 알 수 있다.

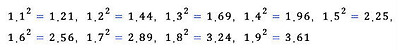
1.41부터 1.49까지 제곱을 해 보면 소수점 아래 둘째 자리가 1이 됨을 알 수 있고, 이런 과정을 계속 반복하면 원하는 정밀도로 근삿값을 구할 수 있다.

조금 더 머리를 쓰자 - 이분법

앞의 방법은 확실하기는 하지만 아무래도 너무 많은 계산을 해야 한다. 계산을 조금 줄이는 방법을 생각해 보자. 우선, 1² = 1 < 2 < 2² = 4이므로 √2=1.**** 꼴이다. 1.1부터 1.9까지 모두 계산하는 대신, 1과 2의 절반인 1.5의 제곱을 계산하여 보면, 1² = 1 < 2 < 1.5² = 2.25이므로, √2는 1과 1.5 사이에 있다. 이번에는 1과 1.5의 절반인 1.25의 제곱을 계산해서 2와 비교하면 다음과 같다.

따라서, √2는 1.25와 1.5 사이에 있다. 앞의 과정을 반복하여, 1.25와 1.5의 절반을 구하면 1.375이고, 1.375를 제곱을 계산하여 2와 비교하면 다음과 같다.

이런 식으로 계속 반복하면, 다음과 같은 결과를 얻을 수 있다.

이 방법은 각 단계마다 부등식의 양 끝 값의 절반을 구하므로 “이분법(bisection method)”이라는 이름이 붙어 있다. 이분법으로 √2를 소수점 아래 세 번째 자리까지 구하려면, 양 끝 값이 1과 2인 경우부터 시작해서 절반을 구하는 과정을 11번 해야 한다. 첫 번째 방법보다는 낫지만, 이것도 그리 빠른 방법이라고 하기는 조금 어렵겠다.

계산기 없이 손으로 구해보자 - 개평법

앞의 방법은 소수 부분이 긴 수를 제곱해야 하므로 계산이 좀 복잡하다. 컴퓨터나 계산기를 쓴다면야 크게 문제될 것이 없겠지만, 종이와 연필만으로 구하기는 어렵다. 모든 계산을 손으로 해결해야 했던 고대 수학자들은 √2의 근삿값을 어떻게 구했을까? 제곱근을 한 자리 구하는 방법 가운데 고대로부터 전해오는 것은 “개평법(開平法)”이라 불리는 알고리즘이다. “개평”은 제곱을 뜻하는 옛날 용어인 평방(平方)을 푼다(開)는 뜻이다. 먼저, 소수 부분을 두 자리 끊어 표시를 한 다음, 제곱하여 2보다 작은 가장 큰 수를 찾는다. 물론 0에서 9가지 정수 중 하나를 고르자는 것이다. 그 값은 당연히 1이고, 나눗셈(長除法)과 비슷한 모양으로 2 위에 1을 쓰고 1×1 = 1을 2에서 뺀다. 뺀 결과 뒤에는 위에 있는 두 개의 0을 내려 쓴다. 한편, 왼쪽에 1+1의 결과를 써 둔다. (그림 ①) 

앞에서 구한 1+1의 결과인 2를 십의 자리로 보고 일의 자리에 넣어 2□×□의 결과가 100을 넘지 않는 가장 큰 수를 찾는다. 이 경우 24×4=96 < 100 < 25×5=125이므로 구하는 수는 4이다. √2의 근삿값은 1.4가 되고, 100에서 24×4를 빼고 뒤에 다시 두 개의 0을 내려 쓴다. 왼쪽에는 24+4의 결과를 써 둔다. (그림 ②)

앞에서 구한 28의 뒤에 붙여서 28□×□의 결과가 400을 넘지 않는 가장 큰 수를 찾는다. 이 수는 1이다. (그림 ③)

281+1=282의 뒤에 붙여서 281□×□의 결과가 11900을 넘지 않는 가장 큰 수를 찾는다. 이 수는 4이다. (그림 ④)

꽤 복잡하지만, 특별한 계산 도구 없이 사용할 수 있는 방법으로서는 비교적 효과적이다.

연분수를 이용하면?

√2에 가까운 유리수를 만드는 방법으로 연분수를 생각할 수 있다. 다음 무한 연분수를 한 단계씩 계산할 때마다 √2에 점점 더 가까워진다.

 

실제로 계산을 해 보면 다음과 같다.

 

1393/985=1.414213197…이므로 소수점 아래 6번째 자리까지 정확하다. 그러나 √x꼴의 무리수를 무한 연분수로 나타내는 과정이 복잡한 경우도 있어서, 근삿값을 구하는 일반적인 방법이 되기는 어렵다.

초고속 계산법 - 뉴튼-랩슨 법

앞서 √2를 계산하는 몇 가지 방법을 알아보았는데, 실은 뉴튼-랩슨 법(Newton-Raphson method)을 이용한 다음의 점화식(漸化式)으로, 간단하면서도 대단히 효율적으로 근삿값을 구할 수 있다. 먼저 x₀의 값을 대충 잡는다. 여기서는 x₀ = 2라 하자. 이제 다음 식을 이용하여 차례로 x_n을 구한다.

이 식은 매우 빠르게 수렴하여, 고작 네 번만 계산해도 x₄=1.4142135623746899⋯을 얻는다. 이 값은 자그마치 소수점 아래 11번째 자리까지 정확하여, 앞의 방법들과는 비교도 되지 않는다. 이 방법은 함수 f(x) = x² - 2의 접선을 반복적으로 그려 원래의 함수가 x축과 만나는 점을 찾는 것으로, 초기값 x₀가 0보다 크기만 하면 어떤 값을 잡더라도 x_n이 빠르게 √2에 가까워진다. 재미있게도, 이 방법은 다른 제곱근을 구할 때도 잘 작동한다. 예를 들어, √2009를 계산하려면, 초기값 x₀을 대충 잡은 다음, 다음 식을 계산하면 된다.

 

40² < 2009 <50² 니까, x₀ = 50으로 두고 계산하면, 다음과 같다. 이 값은 소수점 아래 21번째 자리까지 정확하다.

 

일반적인 함수의 근을 구하는 것은 뉴튼이 미적분학을 창안하면서 개발한 것이지만, 제곱근을 구하는 위의 방법은 고대 수학자들도 알고 있었다. 바빌로니아의 점토판에 남아있는 근삿값도 이 방법을 사용한 것으로 추정된다. 이런 이유로 제곱근을 구하는 위의 방법을 “바빌로니아 방법(Babylonian method)”이라고도 한다.

글 박부성 / 경남대학교 수학교육과 교수 

서울대 수학교육과를 졸업하고, 서울대 수학과에서 석사, 박사 학위를 받았다. 현재 고등과학원 연구원을 거쳐 현재 경남대학교 수학교육과 교수로 재직 중이다. 저서로는 <재미있는 영재들의 수학퍼즐>, <천재들의 수학노트>가 있다.