자연수 vs 유리수

[귀뚜라미]

짝수 집합이나, 소수(prime number)의 집합, 정수 집합 모두 셀 수 있는 집합, 즉, 자연수와 기수가 같은 집합이다. 그렇다면 정수보다 훨씬 큰 집합인 유리수 집합은 어떨까?

자연수의 순서쌍과 자연수의 기수가 같다 (1)

'자연수 vs. 정수' 글과 같이 이번에도 힐베르트 호텔의 비유를 가지고 얘기를 시작해보자. '무한개의 방이 있으나 빈 방이 없다'는 힐베르트 호텔의 명성이 자자해지자, 우후죽순처럼 유사한 호텔이 생겨났다. 힐베르트 호텔 2호점, 3호점, 4호점, …이 차례로 생기더니, 급기야 무한개의 힐베르트 호텔이 생겼다. 모든 힐베르트 호텔에는 손님이 꽉꽉 들어차 있었는데, 힐베르트 호텔 단합회때문에 모든 손님이 힐베르트 호텔 본점(1호점)에 모여 방을 내달라고 요구하기에 이르렀다. 과연 힐베르트 호텔은 이번에도 모든 손님들에게 방을 내줄 수 있을까?

이런 상황을 수학 용어를 써서 표기해 보자. m호점 n호실에 있던 손님을 (m, n)으로 표기하기로 하자. 즉 자연수 순서쌍의 집합 N×N을 생각하자는 것이다.

N×N은 아래 왼쪽 그림에 나타낸 것처럼 가로줄과 세로줄이 만나는 점(격자점이라 부른다)들의 집합이다. 가로줄마다 세로줄과 자연수 개수만큼 만나는 데, 가로줄이 무한개 있으므로, 이런 의미에서 자연수 집합을 자연수개만큼 합집합한 것으로 이해할 수 있다. 겉보기에는 이런 격자점의 수가 자연수보다는 대단히 많을 것으로 보이지만, 아뿔싸. 이 집합도 N과 기수가 같다! 예를 들어 아래 오른쪽 그림처럼 좌하귀부터 시작하여 왼쪽 대각선을 따라 1번부터 번호를 붙여줄 수 있기 때문이다.

즉, 다음과 같이 대응하는 것이다.

모든 격자점에 빠짐도 없이, 중복도 없이 1, 2, 3, 4, … 번호가 붙는 것을 알 수 있다. 일반적으로 (m, n)에 대응하는 자연수가 다음과 같음을 확인할 수 있다.

예를 들어 격자점 (4, 2)에는 (4+2-1)(4+2-2)/2 + 4 = 14라는 번호가 붙음을 확인할 수 있다. 즉, 힐베르트 호텔 4호점 2호실에 묵었던 손님은 14호실로 보내면 된다. 한편 위의 그림을 보면 역으로 17이라는 번호는 격자점 (2, 5)에 붙는 걸 알 수 있다. 즉, 새로 17호실에 묵게 될 손님은 이전에는 2호점 5호실에 묵던 손님이다. 애초부터 힐베르트 호텔은 1호점 하나면 이 모든 손님을 충분히 수용할 수 있었다는 얘기니, 불필요하게 호텔을 더 지을 필요가 없었던 것이다.

자연수의 순서쌍과 자연수의 기수가 같다 (2)

하지만 위와 같은 대응을 할 경우, 예를 들어 2010호실에 있던 손님이 원래 어디에 묵던 손님인지 계산하는 다소 귀찮은 일이 생겼다. 즉, 세월이 지나 기억이 희미해진 손님들에게 예전에 몇 호점 몇 호실에 묵었는지 물어보면 대답하기가 힘들다는 얘기다. 각 격자점에 어떤 자연수가 할당되는지, 혹은 주어진 자연수가 어떤 격자점에 해당하는지 비교적 계산하기 쉽게 붙이는 방법도 있다. 오른쪽 그림처럼 붙여 나가는 것이다. 규칙이 보이는가? 어떻게 숫자를 부여했는지 눈여겨보라. (m, 1)에는 1, 2, 4, 8, …처럼 2의 거듭제곱  2m-1을 붙이고, (1, n)에는 1, 3, 5, 7, …처럼 홀수 2n-1을 붙인다. 일반적으로는 격자점 (m, n)에는 이 두 수의 곱인  2m-1×(2n-1)을 붙인다. 이렇게 하면 모든 자연수를 중복도 없이, 남김도 없이 붙일 수 있다!

이런 대응을 하면, m호점 n호실에 투숙했던 손님은 2^m-1×(2n-1)호실로 찾아가라고 하면 된다. 예를 들어 5호점 2호실에 투숙했던 손님은 2⁴×3=48호실로 찾아가면 된다.  반대로 예를 들어보면, 2012호실에 있던 손님은 2012=2^3-1×(2×252-1)이므로, 3호점 252호에 묵었던 손님임을 쉽게 알 수 있다.

자연수와 양의 유리수는 개수가 같다 (1)

자연수나 정수나 셀 수 있는 집합이다. 자연수보다 기수가 더 큰 집합의 후보로 유리수의 집합이 있다. 양의 유리수의 집합을 Q라 하면, Q의 원소는 항상 기약분수로 나타내어 n/m 꼴로 쓸 수 있는데, (m, n은 서로 소인 자연수) 이 수를 좌표 평면에서 (m, n)에 대응하자. 예를 들어 유리수 1.25는 기약 분수로 쓰면 5/4이므로 좌표 평면에서 (4, 5)에 대응하자는 뜻이다. 그러면 위에서 NxN이 이루는 격자점 중에서 일부분을 뺀 점들이 대응한다. 조짐이 이상하다. 유리수의 개수가 격자점의 개수보다 모자란다는 얘긴데, 위에서 보았듯이 격자점의 개수는 자연수의 개수와 같지 않았던가?

불길함은 현실로 나타난다. 앞서 격자점에 자연수를 부여한 것과 비슷한 방법으로 숫자를 붙이는데, 이번에는 m, n이 공약수를 가지는 격자점 (m, n)을 건너뛰며 붙이면 된다. 즉, 오른쪽 아래 그림처럼 대응하자는 것이다.

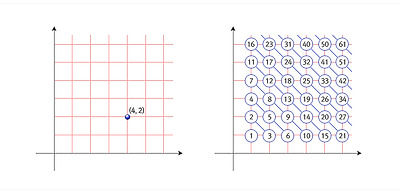
굳이 나열하자면 다음과 같이 하자는 뜻이다.

양의 유리수와 자연수 사이에 일대일 대응을 찾았으니, 음의 유리수와 음의 정수 사이에도 일대일 대응을 찾을 수 있다. 0을 0에 대응해주면, 유리수 전체와 정수 사이에 일대일 대응을 찾을 수 있다. 그런데 정수와 자연수 사이에는 일대일 대응을 이미 찾을 수 있으므로, 유리수 전체와 자연수 사이에도 일대일 대응을 찾을 수 있다. 따라서 유리수 집합은 여전히 셀 수 있는 집합이다.

자연수와 양의 유리수는 개수가 같다 (2)

그런데 위의 방식으로 번호를 붙이면, 예를 들어 2010이 어느 격자점에 붙는지 계산하는 건 무척 귀찮은 일이다. 역으로 예를 들어 유리수 13/27에 붙는 자연수가 무엇인지 계산하려면 골치가 아프다. (독자들은 이런 계산 문제를 만난 경험이 있거나, 앞으로 만날 가능성이 많다.) 그런데 깔끔하면서도 뜻밖에 알려지지 않은 일대일 대응이 있어 소개하려고 한다.

M을 {0, 1, 2, 3, …}이라 하고, 정수의 집합을 Z라 할 때, m이 짝수이면 m/2, m이 홀수이면 –(m+1)/2로 준 함수 f : M→Z는 일대일 대응임을 어렵지 않게 확인할 수 있다.

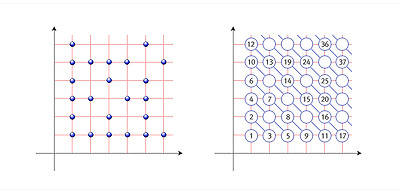
이제 자연수 n에 양의 유리수를 다음처럼 대응하자.

예를 들어 자연수 2009를 인수분해하면, 2009=7²×41¹이다. 따라서 2009에는 양의 유리수 q=7^f(2)×41^f(1)=7¹×41^-1, 즉, 41분의 7을 대응한다. 역으로 양의 유리수를 아무 거나 가져오더라도 대응하는 자연수를 찾아낼 수 있다. 예를 들어 유리수 20/51은 4×5/(3×17), 즉, 2²×3^-1×5¹×17^-1로 쓸 수 있다. 위의 대응관계로부터 이 수는 2⁴×3¹×5²×17¹에 대응하는 수임을 알 수 있다. (사실 f(0) = 0인 아무 일대일 대응 f : M→Z를 가져오더라도 위에 준 대응은 항상 일대일 대응이 된다.) 이 대응은 독특한 성질도 지니고 있지만, 이 이상은 소개하지 않기로 한다.

이 대응은 필자가 2001년에 발견하여 학술지에 투고했다가 게재가 거절되는 아픔을 겪었다. 필자보다 앞서 1989년에 위와 같은 대응을 발견한 사람이 있었다는 것을 나중에 알게 되어 아쉬워했던 기억이 난다. 자연수와 유리수의 기수가 같다는 것을 칸토어가 밝힌 지 100년이 지나도록 이렇게 간단한 대응이 발견되지 않았다니 기이하기까지 하다. 그럼에도 널리 알려지지 않은 것을 다소 유감으로 생각해 왔는데, 이번 기회에 소개하게 되어 게재 거절의 아픔을 (안 겪어본 사람은 모른다.) 조금이나마 덜 수 있을 것 같다.

아무래도 모든 무한집합은 개수가 같은 것 아닐까?

무한집합 얘기를 3회나 우려먹으면서 도무지 자연수를 못 벗어나고 있다. 모든 무한집합은 자연수와 일대일 대응을 이룰 수 있지 않을까라는 생각이 드는 건 자연스럽기까지 하다. 그렇다는 것을 증명할 수만 있다면야 모든 무한집합은 그냥 ∞라는 기호 하나로 기수를 표기할 수 있을 것이다. 아마도 칸토어도 처음에는 그런 생각을 했을 것이다. 그래서 모든 무한 집합 사이에 일대일 대응을 만들어보려고 노력했을지도 모른다. 그런데 그게 아니었다! 갈수록 태산인 무한집합의 개수 이야기는 다음 회에도 이어진다.

글 정경훈 / 서울대 기초교육원 강의교수