자연로그

[귀뚜라미]

로그의 발견-상용로그의 글에서 기하학적으로 정의한 로그와 상용로그가 탄생한 배경에 대해 살펴봤다. 브리그스가 로그표를 만들어서 계산을 쉽게 만들었다고 했는데, 그렇다면 로그표는 어떻게 만든 걸까? 남들의 계산을 줄이기 위해 브리그스 본인은 수많은 계산을 해야만 했다. 먼저 브리그스가 어떤 계산을 했는지부터 살펴보자.

로그표는 어떻게 만들까?

전에 자연상수 e의 출신을 설명한 글에서, 브리그스가 10의 거듭제곱, 10의 거듭제곱의 거듭제곱을 여러 줄 계산했음을 언급했고, 브리그스가 그런 계산을 한 이유를 설명하겠다고 했는데, 이제 그 시기가 무르익은 것 같다. 브리그스의 상용로그를 log라고 쓰기로 하면, 계산 결과로부터 다음을 얻는다.

      

예를 들어 log(2)를 계산해보자. 첫 번째 줄과, 두 번째 줄로부터 log(2)는 1/4과 1/2 사이의 값이다. 그런데 2를 1.7782794100 38922…로 나누면 1.124682650380698…이다. 로그가 나눗셈을 뺄셈으로 바꿔준다는 사실로부터 다음을 얻는다.

 

이다. 마찬가지로 계속한다. log(1.12468 26503 80698…)는 네 번째 줄과 다섯 번째 줄 사이의 값이다. 1.12468 26503 80698…를 1.07460 78283 21317…로 나누면 1.04659 82293 62989…이므로 다음처럼 쓸 수 있다.

               

마찬가지 과정을 반복하면 log(2) = 1/4 + 1/32 + 1/64 + log(1.00961 31433 33494…)이다. 이런 식의 계산을 통해 log(2) = 1/4 + 1/32 + 1/64 + 1/256 + …=0.3010…을 얻는다. 어이쿠. 이렇게 계산해서야 log(3), log(4), log(5), …를 언제 다 구한다지? log(3), log(7), log(11) 등은 어쩔 수 없이 따로 구해야 하지만, 로그의 성질을 이용하면

                                  

등등을 알 수 있므로 이미 계산한 것을 이용할 수 있다. 눈치 빠른 독자들이라면 소수(素數) p에 대해 log(p)만 계산하면 모든 자연수에 대해 log 값을 계산할 수 있다는 것을 알 것이다. 브리그스는 변변한 계산기도 없던 시절에 10년간 계산을 하여 로그표를 만들었다. 요즘에야 계산기에 숫자 입력하고, 버튼 몇 개만 누르면 끝나는 일이지만, 브리그스 이후 수학도 많은 발달을 거듭해 더 좋은 계산법이 나온 덕택임을 잊어서는 안 된다.

자연 로그

네이피어가 로그를 발명하고, 브리그스가 상용로그의 개념을 만든 후에도, 요즘처럼 정의하는 로그의 개념은 만들어지지 못했다. 이런 상황에서 오늘날 자연 로그(natural logarithm)라 부르는 조금 색다른 방식으로 정의하는 로그가 등장한다. 여기서 우리는 아이작 뉴턴을 만나게 된다. 뉴턴은 자신이 발명한 미적분학을 써서 구간 [1, a]에서 곡선 y=1/x과 x축으로 둘러싸인 부분의 넓이를 ln(a)라 할 때, ln 역시 로그와 동일한 성질을 가짐을 증명했다.

ln(x)는위 그림에 표시한 면적으로 정의할 수 있다.

 

즉, 다음처럼 곱셈을 덧셈으로 바꿔주는 함수를 넓이를 이용해서도 정의할 수 있다는 걸 발견한 것이다.

     

가능하면 미적분의 개념을 사용하지 않고 그 이유를 설명해 보기로 하겠다. ln(ab)는 구간 [1, ab]에서 y=1/x과 x축으로 둘러싸인 부분의 넓이이다. 그 중에서 아래 그림에서 파란색으로 칠한 부분처럼 구간 [a, ab] 사이에서 곡선 y=1/x 과 x축으로 둘러싸인 넓이를 S라 부르자. 이 때, ln(ab) = ln(a) + S임은 당연하므로, S = ln(b)라는 것을 증명하라는 얘기다.

왼쪽 그림의 파란색 영역을 x축 방향으로 a배 줄이고 y축 방향으로 a배 늘리면
오른쪽 그림의 파란색 영역이 된다. 따라서 양쪽의 면적이 같다.

 

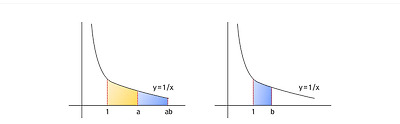
영역 S를 x축 방향으로 a배 줄이고 y축 방향으로 a배 늘려도, 영역의 넓이는 변하지 않을 것이다. 그런데 곡선 y = 1/x는 x축 방향으로 1/a배, y축 방향으로 a배 해도 여전히 y = 1/x이다! 따라서 오른쪽 그림의 파란색으로 칠한 부분의 넓이인 ln(b)와 같아진다!

대수적으로 정의하는 로그의 등장

기하학 혹은 해석학을 써서 정의하지 않고, 지수함수를 이용해서 대수적으로도 로그를 정의할 수 있다는 것을 깨달은 사람은 존 월리스(John Wallis)와 요한 베르누이(Johann Bernoulli)다. 1685년과 1694년의 일이니, 로그 발견 후 거의 80년이나 지난 후의 일인데 다소 의외라는 생각이 들 수도 있겠다. 하지만 실수 지수를 정의하는데 꼭 필요한 ‘극한’의 개념이 제대로 정착돼 있지 않던 시절임을 감안해보면 일견 수긍할 수도 있을 것이다. 아무튼 이들의 발견에도 불구하고 지수함수를 이용한 로그는 그다지 잘 활용되지는 않았는데, 슈퍼스타 오일러가 등장하면서 모든 게 바뀐다. 오일러가 자신의 저작을 통해 지수함수를 이용한 로그를 널리 알리고, 적극 활용한 것이다. 오일러의 명성과 업적 덕택에 이후로는 대수적 방법으로 정의한 로그가 표준을 자리잡았는데, 대수적으로 정의한 로그가 무엇인지 간단히 살펴보기로 하자.

밑이 a인 로그

고정된 양수 a와 (a가 1인 경우는 제외한다) 임의의 실수 x에 대해 지수 a^x를 정의한 바 있다. 이 때, a^x는 모든 양수를 단 한 번씩 값으로 취하는 함수다. 거꾸로 생각하면 양수 b에 대해 a^x=b인 x가 단 하나 있다는 얘긴데, 그 값을 log_a(b) 라고 부른다. 예를 들어, 2⁸=256이므로, log₂(256)은 8이다. 일반적으로 말하면

이 때, a를 ‘밑’이라 부르고, b는 ‘진수’라 부르는데, 조금 유식한 표현으로는 ‘밑이 a인 지수함수와 밑이 a인 로그함수는 서로 역함수 관계’다. 즉, 다음이 성립한다는 뜻이다.

                  

별 것 아닌 것 같은 관계지만 이로부터, 로그 문제가 어려우면 지수 문제로 바꾸어 풀고, 반대로 지수 문제가 어려우면 로그 문제로 바꾸어 풀 수 있다는 걸 알 수 있다. 또한 지수함수의 성질을 이용하여, 로그의 성질을 증명할 수 있다는 장점이 있다. 예를 들어 곱셈을 덧셈으로 바꾼다는 로그의 기본 성질은 다음 식을 보면 알 수 있다.

     

기존의 로그의 재해석

여기서 잠깐. 네이피어의 로그, 상용로그, 자연로그는 새롭게 정의한 로그와 무슨 관련이 있을까? 네이피어의 로그를 정의할 때 등장한 선분의 길이 AB가 10⁷이고 PB가 x인 경우, 네이피어의 로그는 -10⁷×log_e(x/10⁷)에 해당한다. (정확한 증명에는 미분의 개념이 필요하다) 네이피어가 AB의 길이를 10⁷으로 잡은 건, 소수점 이하 일곱 자리 근삿값 대신 정수를 쓰기 위해서, 즉, 0.1234567처럼 소수를 생각하는 대신 1234567을 쓰고 싶어서였다. 그냥 AB의 길이를 1로 잡았다면 그가 발명한 로그는 -log_e(x)에 해당한다. 즉, 자연상수 e가 밑인 로그와 본질적으로 같다. 물론 네이피어는 e의 존재를 몰랐지만, 이런 의미에서 자연상수 e를 네이피어 상수라고도 부르는 것도 적절해 보인다. 한편 브리그스의 로그는 밑이 10인 로그 log₁₀(x)와 동일하며, 뉴턴의 자연로그는 밑이 e인 로그 log_e(x)와 동일하다.

글 정경훈 / 서울대 기초교육원 강의교수